Abstract
Scalable graph states are essential for measurement-based quantum computation and many entanglement-assisted applications in quantum technologies. Generation of these multipartite entangled states requires a controllable and efficient quantum device with delicate design of generation protocol. Here we propose to prepare high-fidelity and scalable graph states in one and two dimensions, which can be tailored in an atom-nanophotonic cavity via state carving technique. We propose a systematic protocol to carve out unwanted state components, which facilitates scalable graph states generations via adiabatic transport of a definite number of atoms in optical tweezers. An analysis of state fidelity is also presented, and the state preparation probability can be optimized via multiqubit state carvings and sequential single-photon probes. Our results showcase the capability of an atom-nanophotonic interface for creating graph states and pave the way toward novel problem-specific applications using scalable high-dimensional graph states with stationary qubits.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Graph states, as well as cluster states, represent a class of multipartite entangled states [1, 2], which provides the resource and lays the foundation for one-way quantum computation [3–5]. This computing scheme builds upon an irreversible flow of measurement outcomes and can be directly mapped to circuit quantum computation with corresponding single- and two-qubit gate operations [4]. Recent progresses have demonstrated generation of the cluster states in diverse platforms including stationary and discrete-variable qubits of a superconducting processor [6, 7], trapped ions [8], trapped atoms in an optical tweezer array [9], and flying photonic qubits encoded in light polarizations [4, 10–15] or continuous variables [16, 17]. For sequentially-woven linear cluster states in time-bin photons [14, 15], only a single setup of single-photon source is required, which is resource efficient but suffers from limited single-photon generation efficiency and state fidelity as the number of qubits scales up.
One of the solutions to improve the generation efficiency is to harness the strong atom-photon coupling in a cavity [15]. This strong-coupling quantum interface has recently shown collective enhancement strength [18, 19], collectively induced transparency [20], and improved metrological gain [21]. The photon-mediated interactions within such systems can further allow four-mode square graph states engineering [22] or W states preparations [23] via state carving technique [24–26]. In particular, an atom-nanophotonic interface [27–29] presents one of the strongly-coupled systems that can host all-to-all dipole-dipole interactions [30], chiral spin-exchange couplings [31–34], intriguing collective radiations [35–43], and topological waveguide quantum electrodynamics [44].
Moreover, a versatile and scalable nanophotonic interface with atoms in optical tweezers envisions a transportable entanglement [45], which promises a coherent atomic quantum processor. Here we propose a scalable generation of arbitrary two-dimensional graph states, including square and linear cluster states, using an atom-nanophotonic cavity platform. This platform has been shown to host strong atom-cavity couplings with tunable waveguide loss parameters for a contrasted single-photon reflectivity [18], where a state carving technique [26] upon reflected photon detections can be used to generate atomic Bell states [45]. Our work here extends the state carving technique to a multi-qubit platform, where we propose new and generic protocols to generate high-dimensional and arbitrary graph states. As an example, we demonstrate the generation of a square graph state in the setup, which promises a potential application in, for example, the measurement-based quantum eigensolver [7, 46]. We also present the essence of the critical coupling regime in an atom-nanophotonic system, which is advantageous in achieving the graph state generations with optimal fidelity and probability. Furthermore, we design a scheme of multiple single-photon probes in such system, which improves the generation probability even when the single-photon reflectivity is not perfectly 100%. This shows the robustness of our protocols which can be facilitated under practical considerations of system variations, for example of imperfections in atom-coupling constants or nonideal contrasted single-photon reflections away from the critical coupling regime.
2. Results
2.1. Atom-nanophotonic cavity
In an atom-nanophotonic interface with a single-sided cavity, Bell states can be prepared via state carving technique [24–26] with contrasted single-photon reflectivity spectra and can be transported to distant places [45], promising a scalable quantum network. The state carving protocol starts from the initialized states  with N = 2 atoms via single-qubit rotations between the atomic coupled state
with N = 2 atoms via single-qubit rotations between the atomic coupled state 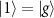 and the uncoupled state
and the uncoupled state 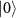 as qubit spaces, where
as qubit spaces, where 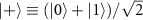 . This leads to a full expansion of four atomic states
. This leads to a full expansion of four atomic states 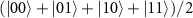 with the number of coupled atoms Na
= 0, 1, 1, and 2, respectively. Here we denote Na
as the number of atoms in the coupled state
with the number of coupled atoms Na
= 0, 1, 1, and 2, respectively. Here we denote Na
as the number of atoms in the coupled state 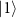 out of a total number N of atoms involved. Through an atom-cavity coupling at the atomic transition
out of a total number N of atoms involved. Through an atom-cavity coupling at the atomic transition  and a relatively high single-photon reflectivity R for at least one of the atoms in the coupled states compared to a low R for
and a relatively high single-photon reflectivity R for at least one of the atoms in the coupled states compared to a low R for 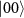 , a weak-field probe projects
, a weak-field probe projects  into
into 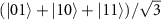 upon a photon detection. This effectively carves out the unwanted component
upon a photon detection. This effectively carves out the unwanted component 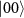 and heralds the bipartite entanglement. The other unwanted component
and heralds the bipartite entanglement. The other unwanted component 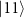 can be removed as well by another state carving, after single-qubit rotations
can be removed as well by another state carving, after single-qubit rotations 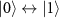 on both qubits, upon again detecting a second probe photon. This two-stage state carving protocol effectively generates an entangled state
on both qubits, upon again detecting a second probe photon. This two-stage state carving protocol effectively generates an entangled state 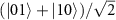 with a probability up to
with a probability up to 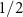 [24] and an optimal state fidelity depending on the maximal and minimal values of R [45].
[24] and an optimal state fidelity depending on the maximal and minimal values of R [45].
Here we consider an atom-nanophotonic interface in a single-sided cavity as shown in figure 1. The Hamiltonians for this system can be written as (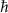 = 1 and see supplementary note 1)
= 1 and see supplementary note 1)
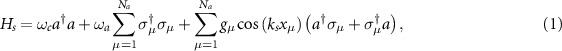
where the atoms are placed at the antinodes of the cavity fields with a profile 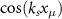 for significant atom-cavity coupling strengths. The system dynamics of the density matrix ρ can be solved from
for significant atom-cavity coupling strengths. The system dynamics of the density matrix ρ can be solved from ![$\dot{\rho} = -i[H_s,\rho]+\gamma \sum_{\mu = 1}^{N_a} D[\sigma_\mu]\rho+\kappa D[a]\rho$](https://content.cld.iop.org/journals/2058-9565/9/2/025020/revision2/qstad33adieqn18.gif) . The cavity resonance frequency is ωc
with a photon operator a, the atomic transition frequency is ωa
with dipole operators
. The cavity resonance frequency is ωc
with a photon operator a, the atomic transition frequency is ωa
with dipole operators 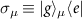 for the ground state
for the ground state 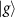 and the excited state
and the excited state 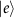 , and an atom-photon coupling constant is g. A number of Na
atoms are coupled with the nanophotonic cavity fields via the evanescent waves above the surface of the waveguide [30, 34], where ks
denotes the wave vector of the guided mode and
, and an atom-photon coupling constant is g. A number of Na
atoms are coupled with the nanophotonic cavity fields via the evanescent waves above the surface of the waveguide [30, 34], where ks
denotes the wave vector of the guided mode and ![$D[c]\rho\equiv c \rho c^\dagger-\{c^\dagger c,\rho\}/2$](https://content.cld.iop.org/journals/2058-9565/9/2/025020/revision2/qstad33adieqn22.gif) with
with 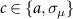 . The total decay rate of the atom is
. The total decay rate of the atom is 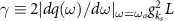 , with
, with 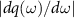 the inverse of group velocity,
the inverse of group velocity,  the resonant wave vector, the coupling strength
the resonant wave vector, the coupling strength 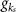 , and the quantization length L. A measure of single-atom cooperativity
, and the quantization length L. A measure of single-atom cooperativity 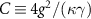 further identifies a strong-coupling regime
further identifies a strong-coupling regime 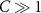 [18] under a total cavity decay rate
[18] under a total cavity decay rate 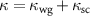 involving the decay rate to the waveguide (wg) and the nonguided rate for scattered (sc) light. This atom-nanophotonic interface can be implemented either with trapped atoms in optical lattices [28] or in optical tweezer arrays [18, 45] as shown schematically in figure 1.
involving the decay rate to the waveguide (wg) and the nonguided rate for scattered (sc) light. This atom-nanophotonic interface can be implemented either with trapped atoms in optical lattices [28] or in optical tweezer arrays [18, 45] as shown schematically in figure 1.
Figure 1. Schematic plot of an atom-nanophotonic cavity. An optical tweezer array of atoms trapped near the waveguide presents a strongly-coupled quantum interface. A single-photon reflectivity measurement can be conducted via collecting the output photon 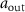 from an input one
from an input one 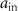 through the atom-photon interactions in a single-sided cavity. An atom-cavity coupling constant is g with a cavity decay rate to the waveguide
through the atom-photon interactions in a single-sided cavity. An atom-cavity coupling constant is g with a cavity decay rate to the waveguide 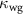 and a loss rate for scattered photons
and a loss rate for scattered photons 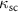 . The γ quantifies the atomic spontaneous emission rate.
. The γ quantifies the atomic spontaneous emission rate.
Download figure:
Standard image High-resolution imageThe single-photon reflectivity  can be obtained by solving the steady-state solutions of
can be obtained by solving the steady-state solutions of ![$\langle A\rangle = \textrm{Tr}[\rho(t\rightarrow\infty) A]$](https://content.cld.iop.org/journals/2058-9565/9/2/025020/revision2/qstad33adieqn45.gif) where
where 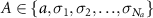 based on the input–output formalism [47] under a weak excitation limit (
based on the input–output formalism [47] under a weak excitation limit (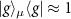 ) with
) with  (see
(see 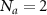 and the reflectivity spectrum for different Na
. We find that when a critical coupling regime is reached [18], that is
and the reflectivity spectrum for different Na
. We find that when a critical coupling regime is reached [18], that is 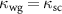 (supplementary note 2), a vanishing R emerges (figures 2(a) and (b)). This suggests the most contrasted single-photon reflectivity which can be utilized to conduct the state carving and project the target states with high fidelity. Meanwhile, this critical coupling regime can be manipulated and controlled by the number of air holes in the region of mirror in the photonic crystal cavity [18, 48, 49]. In particular, a pattern of 500 devices have been created, where a range of loss rates from 2 to 30 GHz can be characterized depending on the number of air holes in the mirror [18]. This offers a versatile platform with wide ranges of nanophotonic cavity properties and makes possible the critical coupling regime we require in this work.
(supplementary note 2), a vanishing R emerges (figures 2(a) and (b)). This suggests the most contrasted single-photon reflectivity which can be utilized to conduct the state carving and project the target states with high fidelity. Meanwhile, this critical coupling regime can be manipulated and controlled by the number of air holes in the region of mirror in the photonic crystal cavity [18, 48, 49]. In particular, a pattern of 500 devices have been created, where a range of loss rates from 2 to 30 GHz can be characterized depending on the number of air holes in the mirror [18]. This offers a versatile platform with wide ranges of nanophotonic cavity properties and makes possible the critical coupling regime we require in this work.
Figure 2. Single-photon reflectivity. (a) The single-photon reflectivity R for 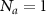 coupled atom is plotted for various
coupled atom is plotted for various 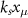 in the cavity field profile
in the cavity field profile 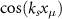 and for various atom-cavity coupling g, under a resonant laser
and for various atom-cavity coupling g, under a resonant laser  at the critical coupling regime
at the critical coupling regime 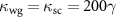 . As
. As 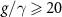 , the on-resonance R approaches its maximum and saturates as g increases, where it becomes more immune to the position variations from the antinodes of the cavity field profile. (b) In this critical coupling regime, a vanishing R for
, the on-resonance R approaches its maximum and saturates as g increases, where it becomes more immune to the position variations from the antinodes of the cavity field profile. (b) In this critical coupling regime, a vanishing R for 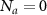 emerges and allows the contrasted reflectivity spectrum compared to the ones for a finite coupled number of atoms Na
under the parameters
emerges and allows the contrasted reflectivity spectrum compared to the ones for a finite coupled number of atoms Na
under the parameters 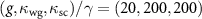 and
and 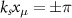 .
.
Download figure:
Standard image High-resolution imageWe note that the on-resonance R in figure 2(a) are robust to the position variations from the anti-nodes of the cavity field profile in the strong coupling regime. On the other hand in the moderate coupling regime, a sensitivity to position fluctuations around the anti-nodes 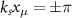 arises [18], which leads to a degradation in the generation probability of graph states but not the fidelity. This fragility can be mitigated by lower the temperature of the atoms in optical tweezers via Raman sideband cooling [50] or gray-molasses loading to optical tweezers [51]. While an adiabatic transport of atoms can manipulate the coupling or uncoupling between the atoms and the cavity photon, which may suffer from atom losses or decoherences [45], an extra qubit state
arises [18], which leads to a degradation in the generation probability of graph states but not the fidelity. This fragility can be mitigated by lower the temperature of the atoms in optical tweezers via Raman sideband cooling [50] or gray-molasses loading to optical tweezers [51]. While an adiabatic transport of atoms can manipulate the coupling or uncoupling between the atoms and the cavity photon, which may suffer from atom losses or decoherences [45], an extra qubit state 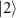 uncoupled to the cavity can be utilized and transferred from
uncoupled to the cavity can be utilized and transferred from 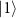 to decouple from the cavity. This only requires a single-qubit gate between
to decouple from the cavity. This only requires a single-qubit gate between  and
and 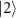 , and should be more resilient to adiabatic transfer errors.
, and should be more resilient to adiabatic transfer errors.
2.2. Generation of linear and two-dimensional graph states
With the contrasted single-photon reflectivity spectrum in the atom-nanophotonic cavity interface, here we propose to generate a special class of multipartite entangled states including linear and two-dimensional cluster states (figure 3). These entangled states establish the foundations for measurement-based quantum computation [3–5, 52, 53]. A graph state is a multipartite entangled state associated with a graph 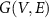 , where V and E stand for the sets of vertices and edges, respectively. The following definition shows the general expression of graph states
, where V and E stand for the sets of vertices and edges, respectively. The following definition shows the general expression of graph states 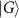 [2] as
[2] as

where 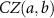 represents the controlled-Z (CZ) gate between qubit spaces spanned by two nodes or vertices a and b linked by edges. Meanwhile, a cluster state denotes a special case of graph states, whose associated graph is a connected subset on cubic lattices [2]. Alternatively, the graph states can be defined equivalently as the common eigenstates of a set of stabilizers
represents the controlled-Z (CZ) gate between qubit spaces spanned by two nodes or vertices a and b linked by edges. Meanwhile, a cluster state denotes a special case of graph states, whose associated graph is a connected subset on cubic lattices [2]. Alternatively, the graph states can be defined equivalently as the common eigenstates of a set of stabilizers 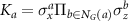 with all eigenvalues of one for all
with all eigenvalues of one for all 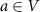 . Here σx
and σz
are Pauli matrices and NG
represents the set of vertices whose elements are in the neighborhood of the vertex a. In terms of the stabilizer formalism, the graph states provide useful and crucial resources for quantum error correction [54].
. Here σx
and σz
are Pauli matrices and NG
represents the set of vertices whose elements are in the neighborhood of the vertex a. In terms of the stabilizer formalism, the graph states provide useful and crucial resources for quantum error correction [54].
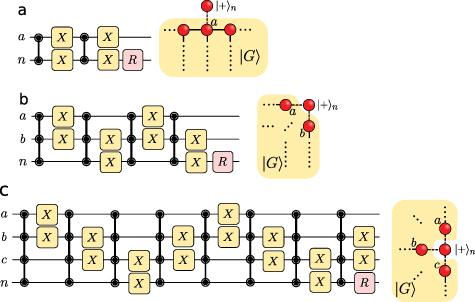
Figure 3. Weaving graph states in one and two dimensions. The graph states can be generated with state carving on the extra qubit 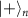 and (a) the qubit node a, (b) the qubit nodes a and b, and (c) the nodes of a, b, and c, in the graph state
and (a) the qubit node a, (b) the qubit nodes a and b, and (c) the nodes of a, b, and c, in the graph state 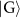 . These represent multiqubit state carvings on
. These represent multiqubit state carvings on  , 3, and 4, respectively. The state carving protocol in (a) provides the foundation to generate the linear cluster states, while all protocols in (a)–(c) and the multiqubit state carving on a larger Na
can generate two-dimensional graph states at arbitrary sizes and shapes. The partially-filled circles with solid links denote the state-carving protocol for Na
atoms. X and R represent the Pauli-X gate and a rotation operation with an angle of
, 3, and 4, respectively. The state carving protocol in (a) provides the foundation to generate the linear cluster states, while all protocols in (a)–(c) and the multiqubit state carving on a larger Na
can generate two-dimensional graph states at arbitrary sizes and shapes. The partially-filled circles with solid links denote the state-carving protocol for Na
atoms. X and R represent the Pauli-X gate and a rotation operation with an angle of  along the y axis, respectively.
along the y axis, respectively.
Download figure:
Standard image High-resolution imageBased on the definition of cluster states in the conventional graph representations, we demonstrate some examples of linear cluster states. For two-node and three-node linear cluster states, they are  and
and 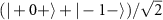 , respectively, as
, respectively, as 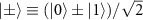 , and CZ gate imprints an extra π phase conditional on the two-qubit states
, and CZ gate imprints an extra π phase conditional on the two-qubit states 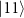 , transforming
, transforming 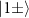 to
to 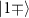 . For four-node linear cluster state, it can be expressed as
. For four-node linear cluster state, it can be expressed as  =
= 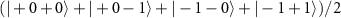 , where a notation of
, where a notation of 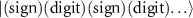 is adopted. Before applying the state carving (SC) protocol for preparing scalable linear graph states
is adopted. Before applying the state carving (SC) protocol for preparing scalable linear graph states  , it would be convenient to rotate them to what we dub the 'precursor' state
, it would be convenient to rotate them to what we dub the 'precursor' state 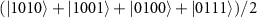 by single-qubit rotations R on the qubit number 1 and 3, respectively (supplementary note 3).
by single-qubit rotations R on the qubit number 1 and 3, respectively (supplementary note 3).
The conventional linear cluster state generation requires a CZ gate on two qubits linking one of the nodes denoted by a in the initial graph state 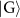 with an extra qubit
with an extra qubit 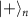 . The resultant new graph state becomes
. The resultant new graph state becomes
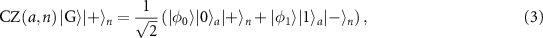
where 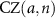 represents the CZ gate operation and the states
represents the CZ gate operation and the states 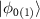 are the graph state components associated with the qubit node a. The resultant graph state is the target state for our proposed protocols using SC in an atom-nanophotonic interface. With a vanishing R for the states
are the graph state components associated with the qubit node a. The resultant graph state is the target state for our proposed protocols using SC in an atom-nanophotonic interface. With a vanishing R for the states 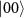 , we obtain the projected and normalized states after SC(a, n) between the qubits a and n upon single-photon reflection,
, we obtain the projected and normalized states after SC(a, n) between the qubits a and n upon single-photon reflection,
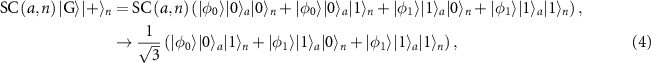
where 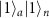 can be rotated to
can be rotated to 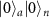 by single-qubit operations and carved out again using SC, transforming equation (4) to the target state of equation (3) up to single-qubit rotations as shown in figure 3(a) (supplementary note 4). This lays the foundation of the protocol for any linear cluster states by weaving the cluster state with extra qubits successively [
by single-qubit operations and carved out again using SC, transforming equation (4) to the target state of equation (3) up to single-qubit rotations as shown in figure 3(a) (supplementary note 4). This lays the foundation of the protocol for any linear cluster states by weaving the cluster state with extra qubits successively [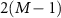 times of SC for M nodes] and for certain two-dimensional graph states like a cross with five nodes or horseshoe cluster states [4].
times of SC for M nodes] and for certain two-dimensional graph states like a cross with five nodes or horseshoe cluster states [4].
To weave general two-dimensional cluster states, we need multiqubit SC on qubits more than 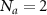 (figures 3(b) and (c)). We take
(figures 3(b) and (c)). We take  in figure 3(b) as an example, and the target state to link the extra qubit
in figure 3(b) as an example, and the target state to link the extra qubit 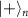 with two edges and two nodes (a and b) in the graph state becomes
with two edges and two nodes (a and b) in the graph state becomes
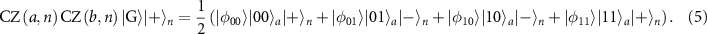
Via four times of SC on the nodes a, b, and n to remove the state component 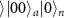 , followed by X gates on (a, b) and (b, n) respectively and successively as in figure 3(b), we obtain (supplementary note 4)
, followed by X gates on (a, b) and (b, n) respectively and successively as in figure 3(b), we obtain (supplementary note 4)
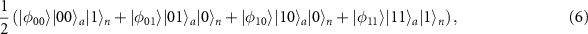
which is exactly the target precursor state and then can be transformed to the target graph state by applying a single-qubit rotation on the nth qubit, fulfilling the protocol to generate graph states more than one dimension (figures 3(b) and (c)). In general, an arbitrary M links with 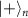 can be achieved by applying the similar designs in the protocols of figure 3. Two arbitrary graph states,
can be achieved by applying the similar designs in the protocols of figure 3. Two arbitrary graph states, 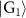 and
and 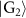 , can also be combined by SC on an additional qubit
, can also be combined by SC on an additional qubit 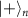 and two nodes in respective graph states. This can be extended to combine arbitrary number of M graph states into a larger graph state with again SC on an additional
and two nodes in respective graph states. This can be extended to combine arbitrary number of M graph states into a larger graph state with again SC on an additional 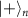 and M nodes with 2M
numbers of SC (supplementary note 4).
and M nodes with 2M
numbers of SC (supplementary note 4).
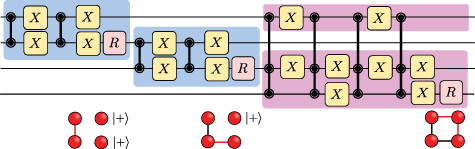
One of the basic elements in two-dimensional graph states is the square graph state. This can be weaved from two one-link qubits and one two-link qubit (figure 4), which results in  . A generic two-dimensional graph state at arbitrary sizes and shapes can then be realized with assistance of multiqubit SC as demonstrated in figure 3. On the other hand, linear graph states can be created only by using 2-atom SC (figure 3(a)), but more exquisite protocols can as well be developed involving multiqubit SC that can improve the optimal probability to generate them, which we discuss more in the next section and in supplementary note 4.
. A generic two-dimensional graph state at arbitrary sizes and shapes can then be realized with assistance of multiqubit SC as demonstrated in figure 3. On the other hand, linear graph states can be created only by using 2-atom SC (figure 3(a)), but more exquisite protocols can as well be developed involving multiqubit SC that can improve the optimal probability to generate them, which we discuss more in the next section and in supplementary note 4.
Figure 4. Square graph state preparation. A series of state carvings on one-link graph state (blue shades) and two-link graph state (purple shades) weave the initialized states 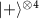 into the square graph state, where intermediate stages of the generated graph states are shown below the circuits.
into the square graph state, where intermediate stages of the generated graph states are shown below the circuits.
Download figure:
Standard image High-resolution image2.3. Probability and fidelity of graph state preparation
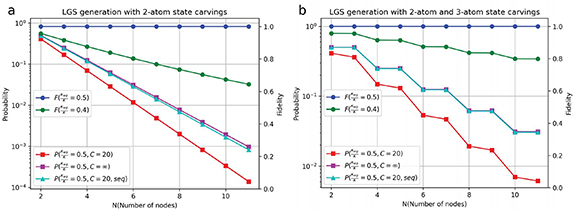
In the following, we investigate the probability and the fidelity of graph state preparation, which can provide insights into the capabilities and limits of the proposed protocols. We also propose an improving protocol by applying a sequential single-photon probe to create optimal probability, high-fidelity, and scalable graph states. A trade-off for our protocol in figure 3(a) is the reduction of the generation probability with the size of the graph state, as more unwanted states need to be carved away. In this regard, we utilize either the multiqubit SC between one node and 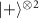 or multiqubit SC among
or multiqubit SC among 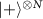 specifically with the digit-sign representation (alternative to sign-digit representation) in the target linear graph states, which optimizes the probability of state preparations with less state components to be carved out (supplementary note 4). We compare the probability and fidelity for linear graph state generation by 2-atom (one node and
specifically with the digit-sign representation (alternative to sign-digit representation) in the target linear graph states, which optimizes the probability of state preparations with less state components to be carved out (supplementary note 4). We compare the probability and fidelity for linear graph state generation by 2-atom (one node and 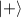 ) and 3-atom state carving (one node and
) and 3-atom state carving (one node and 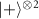 ) protocols in figure 5. The maximum probability P of generating linear graph states in each protocol can be achieved for the ideal case of an infinite cooperativity (i.e.
) protocols in figure 5. The maximum probability P of generating linear graph states in each protocol can be achieved for the ideal case of an infinite cooperativity (i.e. 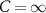 and
and  ), which yields
), which yields 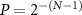 and
and 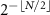 with a floor function of
with a floor function of 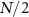 , respectively, showing the advantage of multiqubit SC. In practice, a finite C would produce a non-unity reflectivity R. For a number of
, respectively, showing the advantage of multiqubit SC. In practice, a finite C would produce a non-unity reflectivity R. For a number of 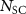 state carvings, a factor of
state carvings, a factor of 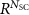 will be multiplied to the probability which quickly decreases as N increases (red squares in figure 5 for C = 20 as an example).
will be multiplied to the probability which quickly decreases as N increases (red squares in figure 5 for C = 20 as an example).
Figure 5. Probability and fidelity of linear graph states (LGS) generations. Two different protocols using 2-atom and multi-atom state carvings are shown in (a) and (b), respectively. The probability at a finite C decreases as the number of nodes N increases, which can be improved for two sequential single-photon probe (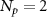 ), approaching the optimized result at an infinite C. The corresponding fidelity is perfect under the critical coupling regime at
), approaching the optimized result at an infinite C. The corresponding fidelity is perfect under the critical coupling regime at 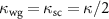 , which degrades as deviating from this regime.
, which degrades as deviating from this regime.
Download figure:
Standard image High-resolution imageTo achieve the maximum probability, we would need to modify the state carving procedure by sending multiple single photons sequentially for each state carving instead of using just one photon each time. This procedure will dramatically decrease the deteriorating effect of non-unity R. For example, the total probability of getting a photon in reflection for Bell state-carving will rise from 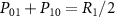 to
to ![$[1-(1-R_1)^{N_p}]/2$](https://content.cld.iop.org/journals/2058-9565/9/2/025020/revision2/qstad33adieqn109.gif) for Np
sequential photons (supplementary note 5), where
for Np
sequential photons (supplementary note 5), where 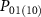 denotes the weighted number of components in the states
denotes the weighted number of components in the states 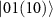 within
within 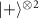 upon single-photon detection. If
upon single-photon detection. If 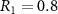 , with just
, with just 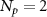 we have
we have 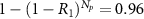 which is near unity, and this dramatically improves the probability to nearly reach the optimal probabilities at an infinite C. For three-atom state carving in figure 5(b), the sequential probability at a finite C is estimated by choosing
which is near unity, and this dramatically improves the probability to nearly reach the optimal probabilities at an infinite C. For three-atom state carving in figure 5(b), the sequential probability at a finite C is estimated by choosing  , showing significant improvement even with an underestimated R3.
, showing significant improvement even with an underestimated R3.
The fidelity of the generated graph states is a deciding factor for measurement-based quantum applications. A high-fidelity graph state indicates genuine multipartite entanglement, which is essential as a resource for one-way quantum computation. The fidelity for generating arbitrarily large graph states becomes perfect when 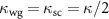 as the critical coupling regime with r0 = 0 (blue circles in figure 5). We note that r0 is the probability of reflection when no atom is coupled to the cavity. All state carvings intend to remove these uncoupled states (i.e.
as the critical coupling regime with r0 = 0 (blue circles in figure 5). We note that r0 is the probability of reflection when no atom is coupled to the cavity. All state carvings intend to remove these uncoupled states (i.e. 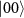 ,
,  , or
, or  states etc). Hence, if r0 = 0, no unwanted state component is projected out when a photon is reflected, resulting in a unit fidelity of the desired state. If
states etc). Hence, if r0 = 0, no unwanted state component is projected out when a photon is reflected, resulting in a unit fidelity of the desired state. If 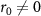 , some unwanted state contribution emerges, and the fidelity deteriorates as seen in the case of
, some unwanted state contribution emerges, and the fidelity deteriorates as seen in the case of 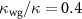 (green circles in figure 5). However, these fidelities can also be improved arbitrarily close to 1 when multiple sequential photons are used. Furthermore, the fidelity is resilient to uneven atom-photon couplings (i.e.
(green circles in figure 5). However, these fidelities can also be improved arbitrarily close to 1 when multiple sequential photons are used. Furthermore, the fidelity is resilient to uneven atom-photon couplings (i.e. 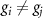 or equivalently
or equivalently 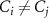 for ith and jth atoms). Therefore, our proposed protocol is robust against multiple forms of imperfections of
for ith and jth atoms). Therefore, our proposed protocol is robust against multiple forms of imperfections of  ,
,  away from the critical coupling regime, and
away from the critical coupling regime, and  for a finite C (supplementary note 5).
for a finite C (supplementary note 5).
As a final remark, we note that the non-unit detector efficiency and dark counts from environment would affect the results presented here. The non-unit detector efficiency would lessen the probability of graph state preparations, while the unwanted dark counts would undermine the fidelity of the generated graph states. Nevertheless, the total detection efficiency is mainly limited by the quantum efficiency of single-photon detector and the fiber taper coupling efficiency, which can be further improved by using superconducting nanowire detectors and a higher fiber coupling efficiency [45], respectively. For the effect of dark counts, a lower ambient temperature can be applied in the system to suppress their influences. We note that the non-unit detection efficiency corresponds to an effectively lower reflectivity R, which can nonetheless be improved by our protocol using multiple single photon probes discussed earlier. Therefore, both of these imperfect operational factors can be made unsubstantial with technical efforts, and our results can be kept intact promisingly.
3. Discussion and conclusion
Our proposed protocol using an atom-nanophotonic interface provides a high-fidelity generation of scalable graph states. We present a general recipe to weave graph states in one and two dimensions, where we provide a multiqubit state carving for linear and two-dimensional graph states at arbitrary sizes. This exquisite design protocol relies on the feature of contrasted single-photon reflection spectra allowed by the critical coupling regime in the interface. Via the state-carving technique, we are able to project the system into the target graph states with high fidelity. A sequence of single-photon probes further enhances the graph state probability, which is especially useful for large-size graph states and promises a near-term application in quantum engineering of multipartite entangled states. Our results illustrate the potential of an atom-nanophotonic cavity for generating linear and high-dimensional graph states, which sets the foundation for measurement-based quantum computation and many intriguing problem-specific applications.
Acknowledgments
We acknowledge support from the National Science and Technology Council (NSTC), Taiwan, under the Grants Nos. 112-2112-M-001-079-MY3 and NSTC-112-2119-M-001-007, and from Academia Sinica under Grant AS-CDA-113-M04. We are also grateful for support from TG 1.2 of NCTS at NTU.
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).
Appendix: Atom–photon coupled equations and input–output formalism
The atom–photon coupled equations can be obtained from the Hamiltonian in equation (1) along with corresponding Lindblad forms. In the Heisenberg picture with the input–output formalism, we have the time-evolving equations of motions,
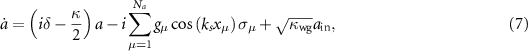
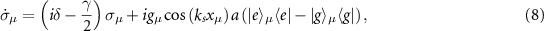
where a photon detuning 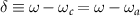 and a Kronecker delta function
and a Kronecker delta function 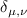 . With a weak probe field at a frequency ω and under the weak excitation limit
. With a weak probe field at a frequency ω and under the weak excitation limit 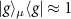 , we are able to calculate the single-photon reflectivity
, we are able to calculate the single-photon reflectivity 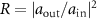 in the steady-state solutions.
in the steady-state solutions.
Supplementary data (1.9 MB PDF)