Abstract
We consider the problem of the magnetization dynamics of a nanosized ferromagnetic sample caused by the spin–orbit interaction of electrons arising in the field of an incident electromagnetic wave. We discuss the case when the frequency of the incident electromagnetic radiation is close to the frequency of the interband transitions. We show that with the use of high-power lasers, this mechanism causes the appearance of a magnetization component perpendicular to the initial magnetization of the sample. This component shows oscillations with a frequency lower than that of incident electromagnetic waves. These dynamics make possible the magnetization reversal of the sample.
Export citation and abstract BibTeX RIS
1. Introduction
The interaction of a strong laser field with the electrons of nanosized ferromagnetic samples has recently attracted significant interest due to the new physics and to possible application of the phenomena caused by this interaction [1, 2]. The magnetization reversal of nanosized ferromagnetic samples is one of the processes that has been studied experimentally and theoretically in the last decade. In particular, this kind of magnetization reversal can significantly improve the performance of storage and magnetic memory devices. However, the explanation of the effect of magnetization reversal caused by the strong laser field is far from complete. One of the works that stimulated further interest in the magnetization dynamics due to the laser pulse is [3], which theoretically predicted the possibility of magnetizing transparent nonferromagnetic samples using circularly polarized radiation.
Later, the magnetization reversal was studied both experimentally [4–6] and theoretically [7–9]. Kirilyuk et al [10] provides a fairly detailed review of works on this topic completed before 2010. As for the most recent works, one can distinguish two main groups. The first group is dedicated to the magnetization reversal of ferromagnets: the spin-valve structure GdFeCo (alloy)/Cu/[Cox Ni1−x /Pt], the Pt/Co/Pt structure, Co/Pt multilayers, and nanoferromagnets [11–16]; the second group concerns ferrimagnets: GdFeCo and Mn2Rux Ga alloys [17–19]. We should also mention the articles containing important information on the mechanisms of magnetization reversal of nanoferromagnets by the field of circularly polarized laser radiation [14, 20–23]. The papers [11, 13, 14] describe the process of magnetization reversal of nanoferromagnets using a single ultrashort laser pulse or minimum pulses.
As shown in [11], the threshold energy density for switching the magnetization of a ferromagnetic layer in a spin valve depends on the duration of the laser pulse, as well as on the thickness and Curie temperature of the ferromagnetic layer. The authors of that study explained most of the experimental results using a phenomenological model. The switching of magnetization in such cases occurs due to the generation of a spin current.
In [13], the two-pulse method for the magnetization reversal of a Pt/Co/Pt ferromagnetic spin valve is studied in detail. Using a combination of a short 90 fs linearly polarized pulse followed by a longer 3 ps circularly polarized pulse, the authors demonstrated that the number of pulses required for complete magnetization reversal can be reduced to four pulse pairs.
Another approach is presented in [14], where the authors discuss all-optical switching in ferromagnetic Co/Pt multilayers, which depends on laser helicity. Here, based on the observation that longer pulses and larger spot sizes lead to increased magnetization reversal efficiency, the authors identify experimental conditions leading to saturated magnetization reversal after just a few dozens of laser pulses. The authors use numerical solutions of the three-temperature model to demonstrate that the all-optical helicity-dependent switching mechanism is based on the spin bath temperature approaching the Curie point.
In [12], where micromagnetic modeling is used, it is shown that the inverse Faraday effect better serves as an explanation for complete optical switching of magnetization than the phenomenon of magnetic circular dichroism.
A numerical study of the all-optical magnetization switching of nanoscale ferromagnetic samples based on the numerical solution of the Landau–Lifshitz–Bloch equation is presented in [16], where the helicity-dependent magnetization reversal is assessed by the magneto-optical effective field caused by the inverse Faraday effect when the sample is exposed to a circularly polarized laser. The effective field contains all the usual terms of the full micromagnetic model: exchange, anisotropy, and Dzyaloshinskii–Moriya interactions.
Recently, a different mechanism of magnetization reversal caused by circularly polarized laser radiation has been proposed [14, 20–23]. In particular, the influence of the laser field on the spin current was analyzed, as well as the fact that heating the magnetic layer decreases its coercive force [20]. These effects facilitate the magnetization reversal of a nanosized sample in an external magnetic field or of a sample whose demagnetizing field is strong enough. The inverse Faraday effect as a non-thermal magnetization reversal mechanism is also studied in [20].
It is noted in [21] that optical excitation of the amorphous ferrimagnetic alloy GdFeCo causes ultra-fast heating of the magnetic system, which makes it very susceptible to a magnetic field simultaneously created by a circularly polarized light pulse. The combination of these two effects leads to magnetization reversal. The condition for the applicability of these mechanisms is the use of ultrashort laser pulses with a duration of about 40 fs.
The main mechanisms responsible for the laser-induced changes in various types of anisotropy—magnetocrystalline, magnetoelastic, interface, and shape anisotropy—are considered in [22].
The following mechanisms of magnetization reversal of nanoferromagnets by a circularly polarized electromagnetic wave are analyzed in [23]: optically induced heating, magnetic circular dichroism, and thermogradient wall motion. These mechanisms operate in a wide temperature range, from at least 50 to 100 K.
Almost all mechanisms of magnetization reversal of nanoferromagnets by a light wave field indicated in articles [14, 20–23] have their limitations. For example, for the joint action of the mechanisms discussed in [20], the injection of a large concentration of non-equilibrium polarized electrons into the magnetic nanolayer is necessary. The condition for the application of the mechanisms outlined in [23] is the use of layered structures made of [Co/Pt]3 multilayers or other structures with sufficiently large domains. Kichin et al [14] proves that the magnetization reversal mechanism indicated by the authors only works with a large number of laser pulses ranging from 10 to 50.
Works [17–19] show that the magnetization reversal caused by a single laser pulse is more easily achieved in nanosized ferrimagnetic samples than in nanoferromagnets. In particular, the possibility of switching the magnetization of a nanosized ferrimagnet with a single laser pulse was experimentally demonstrated in [18].
Here, we consider another method of magnetization reversal in nanosized samples. In our previous article [24], it was clearly shown that the spin-orbit coupling (SOC) of electrons with the electric field of an incident electromagnetic wave is a fairly effective mechanism for the magnetization reversal of nanosized ferromagnetic samples. In particular, the resonance character of the dependence of the induced magnetic moment on the frequency of the radiation is found. The present work considers this mechanism under resonance conditions when the standard nonstationary perturbation theory is inapplicable. The resonance condition is determined by the special relation between the parameters of the band structure and the incident radiation frequency. In our case, the resonance frequency is close to the frequency of interband transitions. In the present work, we discuss this mechanism for the resonance condition by applying the related version of perturbation theory [25].
2. Hamiltonian of the problem and the calculation of magnetization dynamics
Let us consider a nanosized ferromagnetic sample (see figure 1) initially magnetized in the direction of the Oz axis. We suppose that the small size of the sample provides for a single-domain magnetic state [26]. Let a circularly polarized plane electromagnetic wave with a frequency located in the optical range fall on the sample. The wave is polarized in the x–z plane. Since such radiation interacts with the conducting electrons of the sample, its magnetization acquires a component in the direction of the Oy axis.
Figure 1. Nanosized magnetized ferromagnetic sample onto which a circularly polarized electromagnetic wave incidents.
Download figure:
Standard image High-resolution imageUnder resonance conditions, when the usual non-stationary perturbation theory is not applicable, we obtain an expression for this component. We also perform an estimation of the magnitude of the component.
We can assume that the incident electromagnetic wave is circularly polarized:
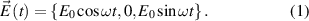
The spin–orbit interaction has the standard form:
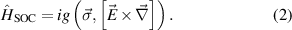
We do not take into account the electron energy operator of the external electric field in the perturbation Hamiltonian, since in our case the spin–orbit interaction of electrons is already included in this energy.
To perform the calculation and to get a numerical estimation, we choose the second model for the band structure of Ni proposed in [27]. The bands in this model are separated by gaps, and numerical estimations of the calculations are rather simple.
We need to solve the Schrödinger equation:
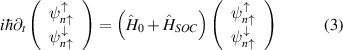
where  is a one-electron Hamiltonian that accounts for the kinetic and potential energies of an electron in the sample, n is the band index.
is a one-electron Hamiltonian that accounts for the kinetic and potential energies of an electron in the sample, n is the band index.
We calculate the wave functions, taking into account only those eigenfunctions  of
of 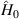 that provide for the resonance interaction with the radiation. In consideration of the Ni band structure in [27], one needs to search the wave functions as a linear combination of four orthonormalized eigenfunctions with time-dependent coefficients:
that provide for the resonance interaction with the radiation. In consideration of the Ni band structure in [27], one needs to search the wave functions as a linear combination of four orthonormalized eigenfunctions with time-dependent coefficients:

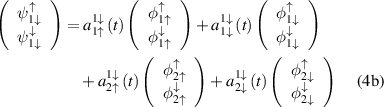
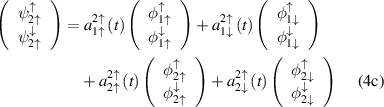

Still, it is enough for the case of resonance interaction to consider only two bands. Below, we use the notation 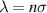 , where
, where 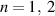 ,
, 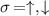 . The time-dependent parts of the eigenfunctions
. The time-dependent parts of the eigenfunctions 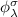 ,
, 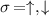 equal
equal 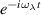 .
.
3. Wave function for the resonance case
Substituting (4) into (3), we get the following equation for coefficients 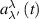 :
:
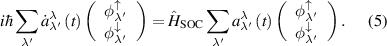
Now, without introducing new notation we redesignate 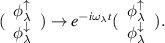
Using orthonormality of these columns, we obtain a system of differential equations for coefficients 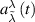 :
:
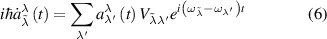
where the matrix elements 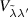 are as follows:
are as follows:
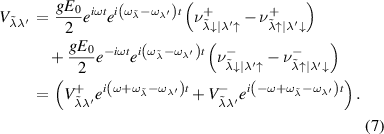
We use the following designations in (7):
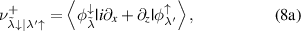
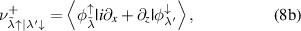

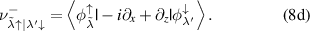
Assuming that only one difference 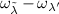 is close to the frequency of the radiation field, we reduce the system of equation (6) to two equations:
is close to the frequency of the radiation field, we reduce the system of equation (6) to two equations:

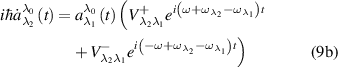
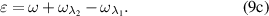
That is,  is a small parameter responsible for the proximity of the electromagnetic field frequency to the resonance frequency
is a small parameter responsible for the proximity of the electromagnetic field frequency to the resonance frequency 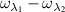 . The common perturbation theory fails under the resonance condition
. The common perturbation theory fails under the resonance condition 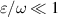 because of the divergence of the perturbation series. The modification of perturbation theory under resonance interaction was considered, for example, in [25]. For the system (9
a) and (9
b), the wave function oscillates between the two initial states. We solve the system of equations (9
a) and (9
b) in full accordance with [25]. We obtain
because of the divergence of the perturbation series. The modification of perturbation theory under resonance interaction was considered, for example, in [25]. For the system (9
a) and (9
b), the wave function oscillates between the two initial states. We solve the system of equations (9
a) and (9
b) in full accordance with [25]. We obtain
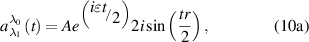
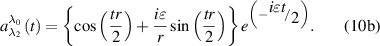
Here, we use the notations
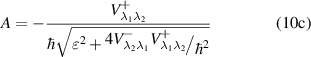
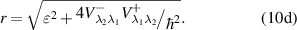
Now, we demonstrate that the interaction of electrons with the laser field leads to the appearance of the y-component my of the magnetization, which is perpendicular to the initial magnetization.
4. Some numerical estimations
For the numerical estimation, we take the band model and the corresponding parameters calculated for Ni in [27]. We consider two electron bands with quadratic dispersion laws and introduce the following notations (see equations (54) and (57) of [27]):

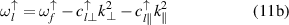

Now  (9
c) obeys the equation
(9
c) obeys the equation

Therefore, we consider two functions of the form 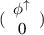 ,
, 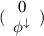 , and the perturbed wave function is a linear combination of these functions:
, and the perturbed wave function is a linear combination of these functions:
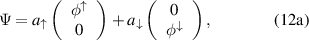
where 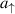 ,
, 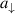 are given by (9a
) and (9b
) with the redesignation
are given by (9a
) and (9b
) with the redesignation  ,
, 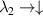 . The upper index
. The upper index 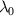 is removed because we now deal with only the wave function.
is removed because we now deal with only the wave function.
We calculate  as
as
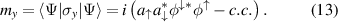
Substituting the coefficients 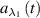 and
and 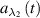 into expression (13), we get the following time-dependent expression for the y-component of the magnetization:
into expression (13), we get the following time-dependent expression for the y-component of the magnetization:
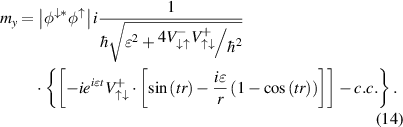
Equation (14) demonstrates that SOC (1) and (2) results in the appearance of a magnetization component perpendicular to the initial direction of the sample's magnetization. This component oscillates with the frequency determined by the matrix element (7) of SOC and does not depend on the frequency of the incident radiation. The amplitude of  depends on this matrix element as well.
depends on this matrix element as well.
To carry out numerical estimations, the expression for 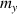 must be integrated over
must be integrated over 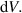 We are interested in the contribution into my
from the states providing for the resonance interaction, that is for small
We are interested in the contribution into my
from the states providing for the resonance interaction, that is for small  . This contribution, since we consider matrix elements (8
a)–(8
d) as k-independent, is reduced to the calculation of a thin layer around the conic surface determined by equation (12), which can be written as
. This contribution, since we consider matrix elements (8
a)–(8
d) as k-independent, is reduced to the calculation of a thin layer around the conic surface determined by equation (12), which can be written as
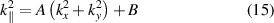
where A and B are constants depending on parameters of the band structure.
Under the resonance conditions, the value of 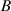 can be neglected. The value of
can be neglected. The value of 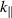 varies within the limits
varies within the limits ![$\left[ { - {{10}^8},{{10}^8}} \right]{\text{ c}}{{\text{m}}^{ - 1}}$](https://content.cld.iop.org/journals/0022-3727/57/25/255003/revision2/dad3377ieqn34.gif) , where the value of
, where the value of 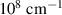 is the cutoff parameter of the band structure. If so, in order to calculate the integral we should multiply three factors: the area of the lateral surface of the cone, the integrand, and factor
is the cutoff parameter of the band structure. If so, in order to calculate the integral we should multiply three factors: the area of the lateral surface of the cone, the integrand, and factor 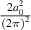 . Taking into account the numerical values of the band parameters of the second model [27] and using simple geometric considerations, we obtain
. Taking into account the numerical values of the band parameters of the second model [27] and using simple geometric considerations, we obtain 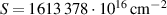 for the area of the lateral surface of the cone.
for the area of the lateral surface of the cone.
As a result, we obtain a resonance value for the magnetization amplitude in the direction of the y-axis. For vanishingly small  , the magnetization doesn't depend on the matrix elements
, the magnetization doesn't depend on the matrix elements 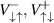 . So, we get
. So, we get 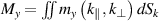 , and
, and 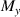 can be as large as
can be as large as 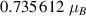 . This is the average magnetic moment in Bohr magnetons per one atom, and, since this value is large enough, the sample can be remagnetized using the currently achievable electric field strengths of circularly polarized laser radiation.
. This is the average magnetic moment in Bohr magnetons per one atom, and, since this value is large enough, the sample can be remagnetized using the currently achievable electric field strengths of circularly polarized laser radiation.
Finally, let us estimate the value of frequency  (10
d) at which the oscillations of
(10
d) at which the oscillations of  occur. In addition, r is the denominator in (14). For the estimation, we set
occur. In addition, r is the denominator in (14). For the estimation, we set 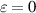 . Then, we estimate the matrix elements
. Then, we estimate the matrix elements 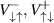 , assuming them to be approximately equal. We note that for various ferromagnetic materials the matrix elements were calculated; for example, in [28, 29]. In accordance with [29], we estimate
, assuming them to be approximately equal. We note that for various ferromagnetic materials the matrix elements were calculated; for example, in [28, 29]. In accordance with [29], we estimate 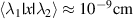 , then
, then 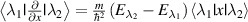 . The value of
. The value of 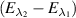 is equal to
is equal to 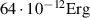 [29]. Then,
[29]. Then,  . Let's set
. Let's set  . Then,
. Then, 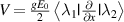 . The SOC constant
. The SOC constant 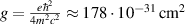 . At currently achievable values of the amplitude of the electric field strength in lasers
. At currently achievable values of the amplitude of the electric field strength in lasers  units of the CGS system, we obtain
units of the CGS system, we obtain 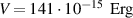 , correspondingly,
, correspondingly, 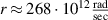 . The frequency r is proportional to E0
, and for the weaker fields the frequency of the oscillations of my
is considerably lower than the frequency of the radiation.
. The frequency r is proportional to E0
, and for the weaker fields the frequency of the oscillations of my
is considerably lower than the frequency of the radiation.
It was noted in [7] that to start the magnetization reversal, we first need to reverse the magnetization in a comparatively small fraction of the sample. Then, due to the exchange interaction, the whole sample will experience the change of the magnetization. Numerical estimation demonstrates that the considered switching mechanism is valid for the field amplitude achieved by modern lasers. Still, the full analysis of the dynamics is more complicated. The dynamics of the magnetization after the radiation disappears are determined by Gilbert damping, magnetic anisotropy, and similar factors. This is a classical problem and the correct incorporation of, e.g., anisotropy energy into the quantum Hamiltonian is hardly a trivial task (see, for instance, [30]). Some experiments [31, 32] show fast and robust magnetization reversal under circularly polarized radiation. At the same time, theoretical analysis in the framework of the Landau–Lifshitz–Gilbert equation admits complicated behavior, including bifurcations and multiperiodic orbits [33]. Our model predicts that my oscillates with a frequency different from the frequency of the radiation. In our opinion, this effect is worth studying experimentally.
5. Conclusion
We have analyzed a new mechanism of possible magnetization reversal in nanosized ferromagnetic samples based upon spin–orbit interaction of the electrons of the sample with an electric field of electromagnetic radiation under the resonance condition. The resonance nature of the interaction is due to the coincidence of the interband transition frequency and the frequency of the incident radiation. We assumed a circular polarization of the incident light and estimated the induced magnetic moment in the direction perpendicular to the initial magnetization. We found that under the resonance condition, the induced magnetic moment shows oscillations with a frequency that can be significantly lower than the frequency of the radiation. The calculated dynamics of the magnetization demonstrate the possibility of magnetization switching. This is the principal difference with our article [24], where the transitions between the bands of the same spin were considered. In the present work, we consider the transition between bands of opposite spins. We demonstrate that my oscillates, and the frequency of oscillations (10d ) can be considerably smaller than the radiation frequency. Therefore, the evolution of magnetization is determined, among other factors, by the magnitude of the component my at the moment the radiation field disappears.
The only requirement for the validity of our model is that the metal has ferromagnetic properties and four electronic bands, in two of which the electrons have one spin direction, and in the other two bands they have a different spin direction. However, in all real ferromagnets, there is always a d-sublevel in the atoms. This means that it is very difficult to find a ferromagnet in which this mechanism is absent. At the same time, as noted in the Introduction, there are several possible mechanisms of magnetization reversal. The proposed mechanism is one of them, and we can assume that in most cases simultaneous action of several mechanisms takes place.
Acknowledgments
A V Lobachev has carried out the mathematical calculations and written this article as a participant of Program No. FFNN-2022-0019 of the Ministry of Science and Higher Education of the Russian Federation for Valiev Institute of Physics and Technology of RAS.
Data availability statement
All data that support the findings of this study are included within the article.


