Variational three-field reduced order modeling for nearly incompressible materials

Abstract

This study presents an innovative approach for developing a reduced-order model (ROM) tailored specifically for nearly incompressible materials at large deformations. The formulation relies on a three-field variational approach to capture the behavior of these materials. To construct the ROM, the full-scale model is initially solved using the finite element method (FEM), with snapshots of the displacement field being recorded and organized into a snapshot matrix. Subsequently, proper orthogonal decomposition is employed to extract dominant modes, forming a reduced basis for the ROM. Furthermore, we efficiently address the pressure and volumetric deformation fields by employing the k-means algorithm for clustering. A well-known three-field variational principle allows us to incorporate the clustered field variables into the ROM. To assess the performance of our proposed ROM, we conduct a comprehensive comparison of the ROM with and without clustering with the FEM solution. The results highlight the superiority of the ROM with pressure clustering, particularly when considering a limited number of modes, typically fewer than 10 displacement modes. Our findings are validated through two standard examples: one involving a block under compression and another featuring Cook’s membrane. In both cases, we achieve substantial improvements based on the three-field mixed approach. These compelling results underscore the effectiveness of our ROM approach, which accurately captures nearly incompressible material behavior while significantly reducing computational expenses.

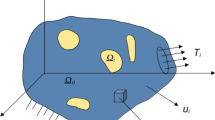
1 Introduction

In recent years, the field of computational mechanics has seen remarkable progress, especially in modeling the behaviors of complex materials. One particular area of focus is the modeling of nearly incompressible materials, such as rubber-like elastomers and soft tissues, which play vital roles in various engineering and biomedical applications which exhibit substantial shape changes while maintaining a relatively constant volume under applied loads resulting in intricate stress–strain relationships that standard finite element methods designed for fully compressible materials struggle to accurately represent [13]. This has led to increased exploration of advanced modeling techniques. These techniques aim to capture material responses of nearly incompressible materials with increased accuracy. Multi-field variational formulations, which introduce additional variables into the problem statement, offer a versatile framework for improving accuracy and robustness [28].

For example, Reese et al. [26] developed a locking-free element for large deformations based on reduced integration and stabilization concepts using enhanced strain methods. Doll et al. [10] proposed selective reduced integration as an effective method to overcome volumetric locking, and Chiumenti et al. [8] presented a mixed three-field formulation to address incompressibility constraints. Nakshatrala et al. [17] introduced mixed stabilized finite element formulations based on a multiscale variational principle to overcome locking issues. Wulfinghoff et al. [30] developed an efficient discontinuous Galerkin element for mitigating locking in large deformation problems.

Reduced Order Modeling techniques have gained attention due to their potential to significantly reduce computational costs while maintaining accuracy. These techniques exploit the underlying structure of the governing equations to represent high-dimensional problems in lower-dimensional subspaces. Various ROM techniques, including Proper Orthogonal Decomposition (POD) [2, 5, 25], Galerkin projection [24, 27], and Reduced Basis Methods (RBM) [12], have been successfully applied in various engineering disciplines.

However, when dealing with nearly incompressible materials, stability and robustness become critical considerations for reduced order models. Traditional ROM techniques may struggle to accurately reproduce the stress–strain behavior of these materials. Ensuring stability while preserving computational advantages is a key research area.

To address this, Niroomandi et al. [18, 19] developed a reduced order model for materials undergoing large strains that reduces the need for the Newton algorithm when searching for stable positions in nonlinearly behaving elastic bodies compared to conventional POD. They also proposed a method for handling geometrically nonlinear models by combining model reduction techniques with an efficient nonlinear solver [20]. Caicedo et al. [4] utilized POD to create a reduced basis from micro-deformation gradient fluctuations, simplifying micro-force balance, stress homogenization, and macro-constitutive tangent tensor equations through Galerkin projection. Radermacher and Reese [23] used POD with empirical interpolation to address non-linear elasticity problems, resulting in faster results than conventional POD methods.

Fresca and Manzoni [11] introduced deep learning-based Reduced Order Models (DL-ROMs), which excel in handling nonlinear time-dependent parametrized partial differential equations (PDEs). Bhattacharjee and Matouš [3] introduced a novel manifold-based reduced order model for addressing nonlinear problems in multiscale modeling of complex hyperelastic materials. Baiges et al. [1] introduced an adaptive finite element-based reduced-order model employing artificial neural networks to correct and enhance simulations with coarse finite element meshes applied to various nonlinear solid mechanics, quasi-incompressible flow, and fluid–structure interaction problems. Wulfinghoff et al. [31] presented a nonlinear homogenization approach using model order reduction through a combination of a Hashin–Shtrikman-type variational principle with data clustering, dividing typical deformation patterns in microstructures into clusters.

Recent literature highlights the efforts of researchers to develop robust reduced order modeling techniques tailored for nearly incompressible materials. These advancements encompass various approaches, including incorporating additional kinematic variables, modifying variational formulations, and leveraging adaptive strategies to enhance accuracy and stability. Furthermore, the integration of machine learning and data-driven techniques with ROM holds promise for addressing challenges related to modeling complex behaviors.

In this context, this paper aims to develop a fast and reliable reduced-order model for nearly incompressible materials. The novelty of this ROM lies in the utilization of pressure clustering within the domain using the k-means algorithm [14, 16], applied to a Hu-Washizu type three-field formulation, initially developed by Simo et al. [29] to model nearly incompressible hyperelastic and elastoplastic materials. This concept was successfully applied to remove volumetric locking from finite element models in the nearly incompressible case. The aim of this work is to investigate the potential of this concept when transferred to reduced-order models.

The paper proceeds as follows: Sect. 2 provides compact equations for nearly incompressible materials, followed by the presentation of the reduced-order model. Section 3 demonstrates the application of the ROM to different examples, and Sect. 4 concludes the paper while suggesting directions for future work.

The notation conventions are as follows: Scalar quantities are presented in light-face italic characters, for example, ‘a’ or ‘A’. First and second-order tensors are denoted using bold-face italic letters, e.g., ‘${\varvec{a}}$’ or ‘${\varvec{A}}$’. Fourth-order tensors are represented using blackboard bold-faced letters, such as $\tiny {\varvec{{\mathbb {C}}}}$ or $\varvec{{\mathbb {C}}}$.

In addition, we denote the transpose of a second-order tensor as ‘${\varvec{A}}^T$’. To represent the symmetric and deviatoric parts of a second-order tensor ‘${\varvec{A}}$’, we use ‘${\textrm{sym}}({\varvec{A}})$’ for the symmetric part $(1/2)({\varvec{A}} + {\varvec{A}}^T)$ and ‘${\varvec{A}}$’ for the deviatoric part $({\varvec{A}} - (1/3){\textrm{tr}}({\varvec{A}}){\varvec{I}})$. Here, ‘${\varvec{I}}$’ signifies the second-order identity tensor, and ‘${\textrm{tr}}({\varvec{A}})$’ represents the trace of ‘${\varvec{A}}$’.

Furthermore, the double contraction of two tensors ‘${\varvec{A}}$’ and ‘${\varvec{B}}$’ is indicated as ‘${\varvec{A}}:{\varvec{B}}$’, while the dyadic product is represented as ‘${\varvec{a}} \otimes {\varvec{b}}$.’ The determinant of a tensor ‘${\varvec{A}}$’ can be designated by ‘${\textrm{det}}({\varvec{A}})$’.

2 Modeling framework

Within the context of a continuous deformable body, characterized by a reference configuration ${{\mathcal {B}}}_0$ and current configuration ${{\mathcal {B}}}$, we define the displacement vector ${\varvec{u}}$. This vector represents the change in position at a given time t of a material point initially located at position ${\varvec{X}}$. Mathematically, this displacement vector is defined as the difference between the point’s current position vector ${\varvec{x}}$ and its reference position vector ${\varvec{X}}$, denoted as ${\varvec{u}}({\varvec{X}},t) = {\varvec{x}}({\varvec{X}},t) - {\varvec{X}}$.

To precisely quantify how infinitesimal line elements are mapped from the reference configuration to the current configuration, we introduce the deformation gradient:

$$\begin{aligned} {\varvec{F}}= \textit{ Grad} ({{\varvec{x}}}({{\varvec{X}}},t))={\varvec{F}} = \frac{\partial {\varvec{x}}}{\partial {\varvec{X}}}. \end{aligned}$$

(2.1)

The local volume change is described by

$$\begin{aligned} \frac{{\textrm{d}}v}{{\textrm{d}}V}=J={\textrm{det}}({\varvec{F}}), \end{aligned}$$

(2.2)

where ${{\textrm{d}}v}$ and ${{\textrm{d}}V}$ denote the volume of an infinitesimal volume element in the reference and current configuration, respectively.

Defining the isochoric part of the deformation gradient as

$$\begin{aligned} \bar{{\varvec{F}}}=J^{-1/3}{\varvec{F}}, \end{aligned}$$

(2.3)

it is easily seen that

$$\begin{aligned} \textrm{det}(\bar{{\varvec{F}}})=1. \end{aligned}$$

(2.4)

The right Cauchy–Green tensor can be represented as follows:

$$\begin{aligned} {\varvec{C}}= {\varvec{F}}^T {\varvec{F}}. \end{aligned}$$

(2.5)

The isochoric part of the right Cauchy–Green tensor can be represented as

$$\begin{aligned} \bar{{\varvec{C}}}={\varvec{I\!\!I\!\!I}}_C^{-1/3}{\varvec{C}}=\varvec{{\bar{F}}}^T \varvec{{\bar{F}}}, \end{aligned}$$

(2.6)

where ${\varvec{I\!\!I\!\!I}}_C= {\textrm{det}}({\varvec{C}})= J^2$.

We assume a decoupled representation of the strain energy density function:

$$\begin{aligned} \psi (\bar{{\varvec{C}}},J) = \psi _{\mathrm{{iso}}}(\bar{{\varvec{C}}})+\psi _{\mathrm{{vol}}}(J). \end{aligned}$$

(2.7)

Then, the second Piola–Kirchhoff stress tensor ${\varvec{S}}$ and its fictitious counterpart can be represented as

$$\begin{aligned} {\varvec{S}}=2\frac{\partial \psi }{\partial {\varvec{C}}} \; \ \bar{{\varvec{S}}}=2\frac{\partial \psi _{\text {iso}}}{\partial \bar{{\varvec{C}}}}, \end{aligned}$$

(2.8)

where ${\varvec{S}}$ is a symmetric tensor and can be converted to the first Piola–Kirchhoff stress tensor by ${\varvec{P}}={\varvec{F}}{\varvec{S}}$.

In the reference configuration, we can express the linear momentum balance as follows:

$$\begin{aligned} \textit{ Div} {{\varvec{P}}} + \rho _0 {{\varvec{b}}} =\textbf{0}, \end{aligned}$$

(2.9)

where ${{\varvec{b}}}$ denotes the body force and $\rho _0$ represents the reference mass density. The boundary conditions are defined by ${{\varvec{u}}}= \bar{{{\varvec{u}}}}$ on $\partial {{\mathcal {B}}}_{0\textit{ u}}$, and $\hat{{\varvec{t}}}={{{\varvec{P}}}{{\varvec{N}}}}$ on $\partial {{\mathcal {B}}}_{0\textit{ t}}$. Here, $\hat{{{\varvec{t}}}}$ signifies a given traction vector, and ${\varvec{N}}$ represents the external normal in the reference configuration.

A variational principle for modeling nearly incompressible materials used in the following was first introduced by Simo et al. [29]. This approach is widely used for the treatment of nearly incompressible materials in finite element simulations.

In contrast to traditional approaches that focus solely on displacement ${\varvec{u}}$ and pressure p, this method introduces a third kinematic field variable, denoted as ${\tilde{J}}$. The related potential is decomposed into isochoric, volumetric and external force components as follows:

$$\begin{aligned} \Pi [{\varvec{u}},p,{\tilde{J}}]= & {} \int _{\mathcal{B}_0}(\psi (\bar{{\varvec{C}}},{\tilde{J}})-p({\tilde{J}}-J))\ {\textrm{d}}V\nonumber \\{} & {} -\int _{\partial {{\mathcal {B}}}_{0t}} \hat{{\varvec{t}}}\cdot {\varvec{u}} \ {\textrm{d}}S - \int _{{{\mathcal {B}}}_\textit{ 0}} \rho _0 \text { } {\varvec{b}} \cdot {\varvec{u}} \text { } \textit{ d}{V}. \end{aligned}$$

(2.10)

The first two terms are dedicated to capturing the behavior of nearly incompressible materials, specifically addressing volume-changing (dilational) deformations. These terms are mathematically formulated using variables $J={\textrm{det}}({\varvec{F}})$, p, and a new variable ${\tilde{J}}$. It’s important to note that the constraint $J={\tilde{J}}$ is enforced by the Lagrange multiplier p often denoted as ’pressure’, where p itself is treated as an independent field variable.

To mitigate the issue of volumetric locking, the Q1P0 element [29] is often employed. With this element, ${\tilde{J}}$ and p are discretized using a discontinuous (element-wise constant) ansatz. This approach allows for the elimination of ${\tilde{J}}$ and p at the element level through a technique known as static condensation.

2.1 Stationarity conditions

The state variables are obtained by solving the following saddle point problem:

$$\begin{aligned} \inf _{{{\varvec{u}}} \in \kappa _u}\sup _{p} \inf _{{\tilde{J}}} \Pi \end{aligned}$$

(2.11)

In this context, $\kappa _u = \{{{\varvec{u}}}: {\varvec{u}}=\bar{{{\varvec{u}}}} \text { on } \partial {{\mathcal {B}}}_{0u} \}$ represents the set of admissible displacement fields that satisfy the specified Dirichlet boundary conditions on $\partial \mathcal{B}_{0u}$. We can derive the weak form of the quasi-static linear momentum balance by performing a variation of the potential with respect to the displacements. After a short derivation, we find (for details see Simo et al. [29])

$$\begin{aligned} \delta _{u} \Pi= & {} \int _{{{\mathcal {B}}}_0} (\varvec{\tau }_{\mathrm{{fic}}}'+pJ {\varvec{I}}):{{\varvec{d}}}_{\delta } \text { } {\textrm{d}} V - \int _{\partial {{\mathcal {B}}}_{0t}} \hat{{\varvec{t}}}\cdot \delta {{\varvec{u}}} \text { } {\textrm{d}} S \nonumber \\{} & {} - \int _{\mathcal{B}_\textit{ 0}} \rho _0 {\varvec{b}} \cdot \delta {{\varvec{u}}} \text { } {\textrm{d}} V=0, \end{aligned}$$

(2.12)

where $\delta {{\varvec{F}}}$ and $\delta {{\varvec{u}}}$ are the variations of the deformation gradient and displacement vector, respectively, $\varvec{\tau }_{\mathrm{{fic}}}=\bar{{\varvec{F}}} \bar{{\varvec{S}}}\bar{{\varvec{F}}}^T$ is the fictitious Kirchhoff stress tensor and ${\varvec{d}}_{\delta } = {\textrm{sym}} (\delta {\varvec{F}}{\varvec{F}}^{-1} )$.

Additionally, by varying the potential with respect to p and ${\tilde{J}}$, we derive the weak equality of J and ${\tilde{J}}$, along with the constitutive equation governing volumetric changes.

Fig. 1

Offline–online concept for model order reduction

The variation with respect to p yields

$$\begin{aligned} \delta _p\Pi =\int _{{{\mathcal {B}}}_0}(J-{\tilde{J}})\delta p \ {\textrm{d}} V=0. \end{aligned}$$

(2.13)

This implies that the additional independent variable ${\tilde{J}}$ is equal to $J = {\det ({\varvec{F}})}$, which represents a kinematic constraint. The variation with respect to ${\tilde{J}}$ gives

$$\begin{aligned} \delta _{{\tilde{J}}}\Pi= & {} \int _{{{\mathcal {B}}}_0} \left( \frac{\partial \psi _{\mathrm{{vol}}}({\tilde{J}})}{\partial {\tilde{J}}}-p \right) \delta {\tilde{J}} \text { } {\textrm{d}} V=0, \end{aligned}$$

(2.14)

$$\begin{aligned}{} & {} \Rightarrow p=\frac{\partial \psi _{\mathrm{{vol}}}({\tilde{J}})}{\partial {\tilde{J}}}. \end{aligned}$$

(2.15)

2.2 Reduced order modeling

Following the solution of a fully resolved FEM model across a broad range of parameter values, snapshots, representing the discrete model’s state variable vectors, are systematically stored in a snapshot matrix. By applying POD to this snapshot matrix, we derive a reduced basis that efficiently captures the system’s behavior through a limited set of displacement modes denoted as $\varvec{\phi }_i(\textbf{X})$, where i ranges from 1 to N. This procedure is also shown in Fig. 1. The POD procedure is comprehensively elucidated in the following seminal works [6, 7, 9, 21, 22].

With this reduced basis in place, we can express the reduced solution for the displacement vector, incorporating mode coefficients $\xi _i(t)$, as follows:

Fig. 2

Reference configuration of the domain with pressure clusters

$$\begin{aligned}{} & {} {{\varvec{u}}}({{\varvec{X}}},t)=\sum _{i=1}^{N} \xi _i (t) \varvec{\phi }_i ({\varvec{X}}) \; \ {\textrm{Grad}} \left( {\varvec{u}}({\varvec{X}},t)\right) \nonumber \\{} & {} \quad =\sum _{i=1}^N \xi _i(t) {\textrm{Grad}} \varvec{\phi }_i({\varvec{X}}). \end{aligned}$$

(2.16)

Further, we decompose ${{\mathcal {B}}}_{0}$ into M subdomains $\mathcal{B}_{0k}$:

$$\begin{aligned} {{\mathcal {B}}}_{0}=\bigcup _{k=1}^M {{\mathcal {B}}}_{0k}. \end{aligned}$$

(2.17)

The authors have opted to adapt the concept of piecewise constant pressure values from Q1P0 element, as introduced by Simo et al. [29], for use in MOR. In the Q1P0 element, we utilize piecewise constant ansatz functions for the pressure p and the kinematic field variable ${\tilde{J}}$. However, in our MOR approach, we employ subdomain-wise constant ansatz functions for p and ${\tilde{J}}$ (Fig. 2), enabling the elimination of these variables at the global level through static condensation.

Now, the state variables for the reduced problem are obtained by solving the following discrete saddle point problem

$$\begin{aligned} \inf _{{\varvec{\xi }}}\sup _{{\varvec{p}}} \inf _{\tilde{{\varvec{J}}}} \Pi \end{aligned}$$

(2.18)

where ${\varvec{\xi }}=({\xi _1, \xi _2,\ldots , \xi _N})^T, {{\varvec{p}}}=(p_1,p_2,\ldots , p_M)$ and $\varvec{{\tilde{J}}}=({\tilde{J}}_1, {\tilde{J}}_2,\ldots , {\tilde{J}}_M)$.

Taking the derivative of the potential with respect to $\varvec{\xi }$ will give the weak form of the linear momentum balance in analogy to (2.10).

Now incorporating the reduced basis into ${\varvec{d}}_{\delta }$ as follows:

$$\begin{aligned} {\varvec{d}}_{\delta }= {\textrm{sym}} ({\varvec{l}}_{\delta })= & {} {\textrm{sym}} (\delta {\varvec{F}}{\varvec{F}}^{-1} )\nonumber \\= & {} \sum _{i=1}^N \delta \xi _i \overbrace{ {\textrm{sym}} (\underbrace{{\textrm{Grad}}{\varvec{\phi }_i}({\varvec{X}}) {\varvec{F}}^{-1}}_{{=}{:} {\varvec{g}}_i})}^{{\varvec{g}}_i^s ({\varvec{F}})}, \end{aligned}$$

(2.19)

will give the reduced weak form:

$$\begin{aligned} \delta _{\xi } \Pi =\sum _{i=1}^{N} \delta \xi _i \underbrace{ \left[ \int _{{{\mathcal {B}}}_0} (\varvec{\tau }'_{\mathrm{{fic}}}+pJ {{\varvec{I}}}):{\varvec{g}}^s_i \textit{ d}{V} - \int _{\partial {{\mathcal {B}}}_{0t}} \hat{{\varvec{t}}} \cdot \varvec{\phi }_i \textit{ d}S - \int _{\mathcal{B}_\textit{ 0}} \rho _0 \text { } {\varvec{b}} \cdot {\varvec{\phi }_i} \text { } {\textrm{d}} V \right] }_{{R_i^u}},\nonumber \\ \end{aligned}$$

(2.20)

where ${\varvec{R}}^u = (R_1^u, R_2^u,\ldots , R_N^u)^T$ is the residual for the reduced problem. Additionally, by varying the potential with respect to changes in ${\varvec{p}}$, we derive the weak equality of J and ${\tilde{J}}$:

$$\begin{aligned} \delta _{p} \Pi= & {} \sum _{k=1}^{M} \int _{{{\mathcal {B}}}_{\mathrm{{0k}}}} (J - \tilde{J_k}) \delta p_k \textit{ d}V=0, \end{aligned}$$

(2.21)

$$\begin{aligned}{} & {} \Rightarrow {\tilde{J}}_k= \frac{1}{{{\mathcal {B}}}_{\mathrm{{0k}}}} \int _{\mathcal{B}_{\mathrm{{0k}}}} J \textit{ d}{V}, \end{aligned}$$

(2.22)

that is ${\tilde{J}}_k$ is equal to J in ${{\mathcal {B}}}_{0k}$ only in an average sense. The variation with respect to $\varvec{{\tilde{J}}}$ results in the constitutive equation for the pressure as follows:

$$\begin{aligned} \delta _{{\tilde{J}}} \Pi= & {} \sum _{k=1}^{M} \int _{{{\mathcal {B}}}_{\mathrm{{0k}}}} \left( \frac{\partial \psi _{\mathrm{{vol}}}}{\partial {\tilde{J}}_k} -p_k \right) \delta {\tilde{J}}_k \textit{ d}{V} \end{aligned}$$

(2.23)

$$\begin{aligned}{} & {} \Rightarrow p_k= \frac{\partial \psi _{\mathrm{{vol}}}({\tilde{J}}_k)}{\partial {\tilde{J}}_k}. \end{aligned}$$

(2.24)

The nonlinear term in the residual ${{\varvec{R}}}^u$ is linearized. The linearization process and the formulation of the tangent moduli can be found in “Appendix 6”.

2.3 Pressure clusters

The purpose of pressure clustering is to aggregate similar pressure values within distinct regions ${{\mathcal {B}}}_{0k}$ of the computational domain. This process is executed following the generation of snapshots of pressure values in each element by running the full-scale model for various parameter sets and load cases. Subsequently, a clustering operation is performed using the k-means algorithm, which groups elements with similar pressure values into separate clusters or regions.

To ensure the effectiveness of this clustering process, it is essential to normalize the pressure data. This normalization step is crucial because pressure values can exhibit significant variations between elements, especially when comparing the pressure values at time step 1 to those at the last time step. The normalized pressure value, denoted as ${\tilde{p}}$, is used to ensure that all elements are on a common scale, facilitating meaningful clustering

$$\begin{aligned} {\tilde{p}}_e=\frac{p_e-{\bar{p}}}{\sigma }, \end{aligned}$$

(2.25)

where ${\bar{p}}=\frac{1}{N_e}\sum _e p_e$ and $\sigma =\sqrt{\frac{1}{N_e} \sum _e (p_e-{\bar{p}})^2}$.

To illustrate this process, consider Fig. 3, which schematically represents the clustering of pressure values for all elements (with index ’e’) at two different time steps, namely timestep 1 and timestep 2. The distinct regions highlighted in the figure correspond to separate clusters.

By performing pressure clustering in this manner, we can effectively group elements with similar pressure responses, enabling a more insightful analysis of the behavior of nearly incompressible materials within different regions of the computational domain.

Fig. 3

2D representation of pressure clustering

3 Numerical examples

In this section, simulation results are presented and the newly developed ROM technique is compared against FEM results utilizing two standard examples.

3.1 Block in compression

The block’s dimensions used in this study are adopted from the work of Reese et al. [26].

The geometric configuration, loading conditions, and boundary constraints of the system are illustrated in Fig. 4. To maintain computational efficiency and symmetry, only one-quarter of the system is discretized, and symmetry conditions are enforced along the planes $x=0$ and $y=0$.

Fig. 4

Dimensions and boundary conditions of the block in compression

Fig. 5

Load cases for the training of the POD

The nodes located at the top of the structure are constrained in both the x- and y-directions. Additionally, a surface load, denoted as f, is applied within one quarter of the top of the block.

The material model employed in this analysis is the hyperelastic Neo–Hookean model:

$$\begin{aligned} \psi (\bar{{\varvec{C}}},J)=\frac{\mu }{2}({I}_{{\bar{C}}}-3)+\frac{\lambda }{4}(J^2-1-2 {\textrm{ln}} J) \end{aligned}$$

(3.1)

where ${I}_{{\bar{C}}}= {\textrm{tr}}\bar{{\varvec{C}}}$ is the first invariant of the isochoric part of the right Cauchy–Green tensor. The material parameters used in this study are set as follows: the shear modulus $\mu$ is set to 80.194 N/mm2, while the first $\text {Lam} \acute{\text {e}}$ parameter $\lambda$ is taken as 40,088 N/mm2, which gives a Poisson’s ratio $\nu$ of 0.499.

For the FEM simulation, reduced integration with hourglass stabilization is applied and a mesh convergence study was carried out to assure mesh convergence.

Figure 5 provides a visual representation of the eight different load cases utilized during the training of the POD technique. These load cases serve as the foundation for predicting various combinations of loading scenarios. The loading for each square region is $f=210$ N in the downward z-direction. For each load case, 200 snapshots are captured and the final snapshot matrix contains 1600 snapshots. By creating a training dataset from these cases, we enable the model to learn and generalize the behavior of the system under diverse loading conditions.

Subsequently, we generate pressure clusters based on the data obtained from these training cases. The pressure clusters are depicted in Fig. 6, and an exploded view is presented in Fig. 7. These clusters highlight regions within the system where the pressure is similar across adjacent elements. In this analysis, we have opted to create eight distinct clusters, each encompassing elements with similar pressure values.

It’s worth noting that the choice of the number of clusters is a critical consideration in relation to the number of displacement modes. Increasing the number of clusters implies that fewer elements are grouped together in each cluster, which can introduce errors when using a lower number of modes for the analysis. However, with a higher number of modes, the impact of clustering becomes less significant, and the results tend to be more accurate. Nevertheless, it’s important to strike a balance between the number of modes and computational effort, as a higher number of modes can increase computational demands.

Fig. 6

Pressure clusters developed based on the loading cases

Fig. 7

Exploded view of the constant pressure subdomains

Figure 8 provides a comparison of the displacements at point A within the compressed block example when the prediction is made for an unseen loading case scenario. The load applied for both the regions is $f=210$ N in the downward z-direction. In this comparison, we consider results obtained from the FEM as well as the MOR technique, both with and without the incorporation of pressure clusters.

In the visualization, the mesh representation of the FEM results is depicted using black lines, while the MOR results, with and without pressure clusters, are shown in white wire-frame representation.

In the left-hand comparison (Fig. 8, left), the deformed meshes of the FEM and MOR results overlap to a significant degree. This overlapping suggests a close correspondence between the two approaches, indicating that the MOR technique with pressure clusters accurately captures the behavior of the compressed block, aligning well with the FEM results.

In contrast, the right-hand figure (Fig. 8, right) reveals noticeable differences between the FEM model and the wireframe representations of the MOR results without pressure clusters. This discrepancy implies that the inclusion of pressure clusters has a positive impact on the MOR outcomes. This effect can be attributed to the presence of clusters. In the incompressible limit, in each integration point of the reduced model (i.e., in each element) the constraint ${\textrm{det}} ({{\varvec{F}}}) =1$ would have to be satisfied. Facing the low number of modes/degrees of freedom, this would mean that the model is severely overconstrained. It is expected that this problem occurs similarly in the nearly incompressible case. Therefore, pressure clusters are introduced in order to reduce the number of ’constraints’ to the number of clusters.

Fig. 8

FEM versus MOR comparison of point A z-displacement. Left: with clusters and right: without clusters

Obviously MOR with clusters is able to closely follow and replicate the FEM solution, even with a relatively small number of displacement modes as shown in Fig. 9.

3.2 Cook’s membrane

In the second example, we delve into Cook’s membrane problem, a classic mechanical scenario. Here, we investigate the behavior of a tapered cantilever beam, as illustrated in Fig. 10. The beam has a fixed left end. In contrast, the right end, is subjected to a vertical traction applied in the positive z-direction. This loading configuration represents a fundamental test case in computational mechanics. Here again, we have considered the hyperelastic Neo-Hooke material model with the same material parameters as discussed in the block in compression.

3.2.1 Comparison of FEM versus MOR with and without clusters for diagonal loading

Figure 11 provides a visual representation of the four distinct load cases utilized in the training via POD, specifically for the diagonal loading case. The (dead) load applied is $f=4.096$ kN for each case in the 4 diagonal directions ($45^{\circ },135^{\circ },225^{\circ }$ and $315^{\circ }$) to obtain 4 different deformations.

Figure 12 provides a graphical representation of the clusters formed for the diagonal load case. These clusters are a result of applying the above described clustering techniques to the data obtained during the diagonal loading scenarios.

To gain a more detailed perspective on these clusters, Fig. 13 presents an exploded view.

Fig. 9

Graphical z-displacement comparison of FEM versus MOR (with and without clusters) recorded at point A

Fig. 10

Dimensions and boundary conditions of the Cook’s membrane example

Fig. 11

Load cases utilized for the training of the POD

Fig. 12

Pressure clusters developed based on the, diagonal load cases

Fig. 13

Exploded view of the constant pressure subdomains

Figure 14 offers a comparison of results obtained from three different approaches: FEM, MOR with clustering, and MOR without clustering for 8 displacement modes. Here, we have made a prediction for the diagonal loading condition generated by applying $f=4.096$ kN along $135^{\circ }$ for FEM and MOR. We intentionally reproduce a load case, which was already seen during training in order to demonstrate the problems of the fully integrated ROM, already in this seemingly simple case.

The FEM results serve as a reference, representing the most accurate and computationally intensive solution to the problem. MOR with clustering demonstrates the capability of the ROM technique to capture the system’s behavior efficiently by simplifying the pressure distribution using clusters. MOR without clustering retains individual pressure values for each element, which may lead to a less accurate predictions under lower number of modes as visualized in Fig. 14.

Figure 14 highlights that there is a noticeable discrepancy between the FEM and the MOR with clusters. To mitigate this discrepancy, an increase in number of modes and pressure clusters can be considered. This enhanced agreement is vividly depicted in Fig. 15, where the FEM and MOR with clusters improves when 10 modes and 10 pressure clusters are taken into account.

3.2.2 Comparison of FEM versus MOR with and without clusters for diagonal loading with $\nu =0.49999$

We present here the comparison between FEM and MOR with and without clusters at $\nu =0.49999$ to justify the importance of pressure clusters, particularly as $\nu$ approaches the incompressible limit.

The load cases utilized in the training via POD are same as in Sect. 3.2.1 We collect 500 snapshots for each diagonal loading case. The (dead) load applied is $f=15.36$ kN for each case in the 4 diagonal directions to obtain 4 different deformations as shown in Sect. 3.2.1. Within this context, we present computations for the diagonal loading condition, achieved by applying a force of $f=15.36$ kN along $135^{\circ }$ for both FEM and MOR with and without clusters. We utilized 10 pressure clusters for MOR with clusters.

The MOR with clusters clearly outperforms the MOR without clusters for $\nu =0.49999$, as illustrated in Fig. 16. Notably, MOR with clusters consistently provides reasonable results even with only 10 modes, a stark contrast to MOR without clusters, where approximately 70 modes are required to achieve a comparable approximation of nearly incompressible behavior. The computational efficiency of our approach is further highlighted in Fig. 17 (left), revealing a rapid increase in computational time as the number of modes grow. This emphasizes the efficiency and practicality of our proposed method, especially when considering the challenging scenario of nearly incompressible materials.

Fig. 14

x-,y- and z-displacement comparison between FEM and MOR (with and without clusters) of point A

Fig. 15

x-,y- and z-displacement comparison between FEM and MOR (with and without clusters) of point A with higher number of modes and pressure clusters

Fig. 16

x-displacement comparison between FEM and MOR (with and without clusters) of point A

Table 1 Speedup factor and error for MOR without clusters

Fig. 17

Left: computational time as a function of the number of modes considered. Right: error comparison between MOR with and without clusters

To quantify the accuracy of these computations, we calculate the error using the following formula:

$$\begin{aligned}{} & {} Error = \sqrt{\frac{1}{N} \sum _{i=1}^N \Vert {\varvec{u}}_i^{MORwoc}-{\varvec{u}}_i^{FEM} \Vert ^2}, \end{aligned}$$

(3.2)

where ${\varvec{u}}_i^{FEM}$ and ${\varvec{u}}_i^{MORwoc}$ (for $i=1,\ldots ,N$) represent the displacement solutions obtained from the FEM and MOR without clusters, respectively, $N$ denotes the total number of nodes. Likewise, the error for MOR with clusters is calculated. We compute the error using Eq. 3.2 for time steps 7, 14, 21, and 28 (of 30 equal time steps in total), followed by averaging these values to obtain the overall error.

These simulations are carried out on an Intel®Core$^{{\textrm{TM}}}$ i7-8850H CPU @ 2.60GHz with 32 GB RAM. The speedup factors obtained for this example are summarized in Table 1.

Figure 17 (right) illustrates that the error is notably small for MOR with clusters even with just 10 modes. In contrast, achieving a comparable level of accuracy for MOR without clusters requires a higher number of modes, leading to longer solution times, as depicted in Fig. 17 (left).

3.2.3 Comparison of FEM versus MOR with and without clusters for rotational load

In this particular analysis, we tackle a more intricate scenario to test the capabilities of MOR with and without the incorporation of pressure clusters. The Poisson’s ratio $\nu$ considered in this example is 0.499. The load cases used for training the POD model are depicted in Fig. 18. The (dead) load applied is $f=4.096$ kN for each case (positive and negative x-direction, positive and negative z-direction and along the diagonal $135^{\circ }$ and $90^{\circ }$).

Following the training phase and the generation of a reduced basis, we proceed to obtain pressure clusters, as illustrated in Fig. 19.

Fig. 18

Load cases for the training of the POD

Fig. 19

Pressure clusters developed based on the loading cases

Fig. 20

FEM versus MOR comparison of point A z-displacement. Left: with clusters and right: without clusters

Fig. 21

Comparison of point A displacement in x-, y- and z-direction between FEM and MOR (with and without clusters)

Now the prediction is made for the application of the rotational load to the xz-plane as shown in Fig. 20. The load is expressed as

$$\begin{aligned} f_x={\hat{f}} {\textrm{cos}}(\omega t) \; \ f_z={\hat{f}} {\textrm{sin}}(\omega t) \end{aligned}$$

(3.3)

where $f_x$ and $f_z$ is the load applied along the x- and z-directions, ${\hat{f}}$ is the magnitude of the load applied in this case which is $f=4.096$ kN and $\omega$ is the angular frequency which is 1 rad/s.

Figure 20 provides a comparison between the FEM and MOR results, both with and without the incorporation of pressure clusters with 8 displacement modes. In the left figure, the black wireframe represents the FEM results, while the white wireframe represents MOR with clusters. In the right figure, the black wireframe also represents the FEM results, while the white wireframe represents MOR results without clusters. Again, the accuracy improvement due to the clustering is clearly visible.

The data recorded at point A is analyzed graphically as illustrated in Fig. 21. The comparison highlights that MOR with clusters closely aligns with the FEM results when considering a lower number of modes for analysis. This agreement demonstrates the effectiveness of MOR with clustering in efficiently capturing the system’s behavior.

3.2.4 Comparison of FEM versus MOR with and without clusters with higher number of modes for rotational load case

In Fig. 22, we compare the displacement in the x-, y-, and z-directions of FEM and MOR, both with and without pressure clusters for the case of 30 modes. In the case of MOR with pressure clusters, 30 clusters are created. These comparisons reveal a close agreement in displacement values among all approaches. This agreement underscores the capability of both MOR techniques, with and without clustering, to accurately capture the system’s behavior when a higher number of modes is considered. It is worth noting that MOR without clusters appears to exhibit a slightly superior performance compared to MOR with clusters. The advantage of pressure clustering becomes evident when considering a lower number of modes.

Fig. 22

Comparison of point A displacement in x-, y- and z-direction between FEM and MOR (with and without clusters) with higher number of modes

4 Conclusions

In conclusion, this study introduces an innovative approach for developing a Reduced-Order Model (ROM) tailored specifically for the analysis of nearly incompressible materials. Our method leverages a three-field variational formulation, effectively capturing the intricate behavior of such materials. The ROM construction process involves solving the full-scale model using the FEM, recording displacement field snapshots, and organizing them into a snapshot matrix. Additionally, Proper orthogonal decomposition (POD) is applied to extract dominant modes, forming a reduced basis for the ROM. We address the pressure field, a critical component, by utilizing the k-means algorithm for clustering. This approach allows us to incorporate the clustered pressure field into the reduced-order model.

Our comparison, involving the ROM with pressure clustering, the ROM without pressure clustering, and the FEM solution, reveals the remarkable superiority of the ROM with pressure clustering. This superiority is particularly evident when considering a limited number of modes, typically fewer than 10 displacement modes. Our findings are validated through two standard examples for nearly incompressible material behavior: one featuring a block under compression and the other focusing on Cook’s membrane. The results underscore the effectiveness of our ROM approach in accurately capturing the behavior of nearly incompressible materials. As an outlook, one may investigate how this pressure cluster based MOR works for large strain elastoplastic materials.

Appendix

1.1 Linearization

Consider the weak form of the linear momentum balance

$$\begin{aligned} G_{\xi }= & {} \int _{{{\mathcal {B}}}_0} \underbrace{(\varvec{\tau }'_{\mathrm{{fic}}}+pJ {{\varvec{I}}})}_{\varvec{\tau }}:{{\varvec{d}}}_{\delta } \textit{ d}{{V}}- \int _{\partial {{\mathcal {B}}}_{0t}} \hat{{\varvec{t}}}\cdot \delta {\varvec{u}} \text { } \textit{ d}S\nonumber \\{} & {} - \int _{{{\mathcal {B}}}_\textit{ 0}} \rho _0 {\varvec{b}} \cdot \delta {{\varvec{u}}} \text { } {\textrm{d}} {V} \end{aligned}$$

(6.1)

$$\begin{aligned}= & {} \int _{\mathcal {B}_0} \varvec{\tau }'_{\mathrm{{fic}}}:{{\varvec{d}}}_{\delta } \textit{ d}{{V}} + \sum _{k=1}^{M} p_k \int _{{{\mathcal {B}}}_{0k}} J {{\varvec{I}}}: {{\varvec{d}}}_{\delta } \textit{ d}{V}\nonumber \\{} & {} \quad - \int _{\partial {{\mathcal {B}}}_{0t}} \hat{{\varvec{t}}}\cdot \delta {\varvec{u}} \text { } \textit{ d}S \nonumber \\{} & {} - \int _{\mathcal {B}_0} \rho _0 {\varvec{b}} \cdot \delta {{\varvec{u}}} \text { } {\textrm{d}} {V}. \end{aligned}$$

(6.2)

Treatment of the volumetric part:

$$\begin{aligned}&{\textrm{d}}(p_k J {{\varvec{I}}} : {{\varvec{d}}}_{\delta })={\textrm{d}} p_k J {{\varvec{I}}} : {{\varvec{d}}}_{\delta } \nonumber \\&\quad + p_k J ({{\varvec{F}}}^{-T} : {\textrm{d}}{{\varvec{F}}}) {{\varvec{I}}}: {{\varvec{d}}}_{\delta }-p_k J {{\varvec{I}}}: \overbrace{\delta {{\varvec{F}}} {{\varvec{F}}}^{-1} {\textrm{d}} {{\varvec{F}}} {{\varvec{F}}}^{-1}}^{{{\varvec{l}}}_{\delta } {{\varvec{l}}}_d} \nonumber \\&\quad +({{\varvec{l}}}_d p_k J {{\varvec{I}}} {{\varvec{l}}}^T_{\delta }):{{\varvec{I}}}\nonumber \\&\quad -p_k J {{\varvec{I}}}: {{\varvec{l}}}_d {{\varvec{l}}}^T_{\delta } \end{aligned}$$

(6.3)

$$\begin{aligned}&= {{\varvec{d}}}_{\delta }:(J {{\varvec{I}}}) \frac{{\textrm{d}} p_k}{{\textrm{d}} {\tilde{J}}_k} \overbrace{\frac{1}{{\Omega }_{0k}} \int _{{\Omega }_{0k}} J {{\varvec{I}}} : {{\varvec{d}}}_d \text { } {\textrm{d}}{V}}^{{=}{:} \langle J {{\varvec{I}}}:{{\varvec{d}}}_d \rangle _k} \nonumber \\&\quad + p_k J ({{\varvec{I}}} \otimes {{\varvec{I}}}) {:}{:} ({{\varvec{d}}}_{\delta } \otimes {{\varvec{d}}}_d)+ ({{\varvec{l}}}_{d} p_k J {{\varvec{I}}} {{\varvec{l}}}^T_{\delta }): {{\varvec{I}}}\nonumber \\&\quad - 2 p_k J {{\varvec{d}}}_{\delta }:{{\varvec{d}}}_d \end{aligned}$$

(6.4)

$$\begin{aligned}&\quad \Rightarrow \int _{{\Omega }_{0k}} {\textrm{d}}(p_k J {{\varvec{I}}} : {{\varvec{d}}}_{\delta }) {\textrm{d}}{V}\nonumber \\&\quad = {\Omega }_{0k} \langle {{\varvec{d}}}_{\delta } : J {{\varvec{I}}} \rangle _k \frac{{\textrm{d}} p_k}{{\textrm{d}} {\tilde{J}}_k} \langle J {{\varvec{I}}}:{{\varvec{d}}}_d \rangle _k \nonumber \\&\quad + {\Omega }_{0k} \langle {{\varvec{d}}}_{\delta } : p_k J ({{\varvec{I}}} \otimes {{\varvec{I}}} - 2 {{\varvec{{\mathbb {I}}}}^s}): {{\varvec{d}}}_d \rangle _k \nonumber \\&\quad + \int _{\Omega _{0k}}({{\varvec{l}}}_d p_k J {{\varvec{l}}}_{\delta }^T):{{\varvec{I}}} {\textrm{d}}{V} \end{aligned}$$

(6.5)

$$\begin{aligned}&\quad \Rightarrow \int _{{{\mathcal {B}}}_{0}} {\textrm{d}}({\varvec{\tau }}: {{\varvec{d}}}_{\delta }) {\textrm{d}}{V} = \int _{{{\mathcal {B}}}_0} \Big [ ({{\varvec{l}}}_d {\varvec{\tau }} {{\varvec{l}}}_{\delta }^T) :{{\varvec{I}}} \nonumber \\&\quad + {{\varvec{d}}}_{\delta } : \Big (p J ({{\varvec{I}}} \otimes {{\varvec{I}}} - 2 {\varvec{{\mathbb {I}}}^s}) + {\tiny {\varvec{{\mathbb {C}}}}}^a_{\mathrm{{iso}}} \text { }\Big ) : {{\varvec{d}}}_d \text { }\Big ] {\textrm{d}}{V} \nonumber \\&\quad + \sum _{k=1}^{M} \frac{1}{{{\mathcal {B}}}_0} \int _{{\Omega }_{0k}} {{\varvec{d}}}_{\delta } : J {{\varvec{I}}} \text { } {\textrm{d}} {V} \text { } \frac{{\textrm{d}} p_k}{{\textrm{d}}{\tilde{J}}_k} \int _{{\Omega }_{0k}} J {{\varvec{I}}} : {{\varvec{d}}}_d \text { }{\textrm{d}}{V} \end{aligned}$$

(6.6)

$$\begin{aligned}&={\textrm{d}} \int _{{{\mathcal {B}}}_0} {\varvec{\tau }} : {{\varvec{d}}}_{\delta } \text { }{\textrm{d}}{V}= {\textrm{d}}_{\xi } G_{\xi } = \sum _{i,j=1}^{N} \delta \xi _i {\textrm{d}} \xi _i \Big ( \int _{{{\mathcal {B}}}} \bigg [({{\varvec{g}}}_i {\varvec{\tau }} {{\varvec{g}}}_i^T) : {{\varvec{I}}}\nonumber \\&\quad + {{\varvec{g}}}_i^s : \Big (p J ({{\varvec{I}}} \otimes {{\varvec{I}}} - 2 {\varvec{{\mathbb {I}}}^s}) +{\tiny {\varvec{{\mathbb {C}}}}}_\mathrm{{iso}}^a \text { }\Big ) : {{\varvec{g}}}_j^s \bigg ] \text { } {\textrm{d}}{V}\nonumber \\&\underbrace{+\sum _{k=1}^{M} \frac{1}{{\Omega }_{0k}} \int _{{\Omega }_{0k}} {\textrm{tr}} ({{\varvec{g}}}_i^s) J \text { } {\textrm{d}} {V} \text { } \frac{{\textrm{d}} p_k}{{\textrm{d}} {\tilde{J}}_k} \int _{{\Omega }_{0k}} {\textrm{tr}} ({{\varvec{g}}}_j^s) J \text { } {\textrm{d}}{V}}_{{{\varvec{k}}}_{ij}^u} \Big ) \end{aligned}$$

(6.7)

where ${{{\varvec{k}}}_{ij}^u}$ is the tangent matrix, subscript M represents the number of subdomain and N represents the number of modes considered. $\tiny {\varvec{{\mathbb {C}}}}^a_{\mathrm{{iso}}}$ is the isochoric part of the consistent tangent moduli (see below) and ${\varvec{{\mathbb {I}}}^s}$ is the symmetric $4^{th}$ order identity tensor.

1.2 Isochoric tangent moduli

Consider [15]

$$\begin{aligned} {\textrm{d}}({\varvec{\tau }}_{\mathrm{{fic}}}:{{\varvec{d}}}_{\delta }')= & {} {\textrm{d}}( \bar{{\varvec{F}}} \bar{{\varvec{S}}} \bar{{{\varvec{F}}}}^T: \overbrace{\delta \bar{{{\varvec{F}}}} \bar{{{\varvec{F}}}}^{-1}}^{{{\varvec{l}}}_{\delta }'})\nonumber \\= & {} \overbrace{\bar{{{\varvec{F}}}} {\textrm{d}}\bar{{{\varvec{S}}}} \bar{{{\varvec{F}}}}^T}^{\bar{\tiny {\varvec{{\mathbb {C}}}}}^a:{{\varvec{d}}}_{d}'}: {{\varvec{d}}}_{\delta }' + {\textrm{d}} \bar{{\varvec{F}}} \bar{{\varvec{F}}}^{-1} {\varvec{\tau }}_{{\textrm{fic}}}: {{\varvec{l}}}_{\delta }' \nonumber \\{} & {} + \bar{{\varvec{F}}} \bar{{\varvec{S}}}: {\textrm{d}} \delta \bar{{\varvec{F}}} \end{aligned}$$

(6.8)

where $\bar{\tiny {\varvec{{\mathbb {C}}}}}^a$ is the fourth order fictitious elasticity tensor and

$$\begin{aligned} {\textrm{d}} \delta \bar{{\varvec{F}}}= & {} {\textrm{d}} \left( \delta (J^{-\frac{1}{3}} {{\varvec{F}}})\right) = {\textrm{d}} \left( J^{-\frac{1}{3}} \delta {{\varvec{F}}} \right. \nonumber \\{} & {} \left. -\frac{1}{3} J^{-\frac{4}{3}} J({{\varvec{F}}}^{-T}: \delta {{\varvec{F}}}) {{\varvec{F}}} \right) = \nonumber \\{} & {} {\textrm{d}} \left( J^{-\frac{1}{3}}\right) \left( \delta {{\varvec{F}}} -\frac{1}{3} {\textrm{tr}} ({{\varvec{l}}}_{\delta }) {{\varvec{F}}}\right) \nonumber \\{} & {} + J^{-\frac{1}{3}}\left( -\frac{1}{3} {\textrm{tr}} \underbrace{({\textrm{d}} {{\varvec{l}}}_{\delta })}_{-\delta {{\varvec{F}}} {{\varvec{F}}}^{-1} {\textrm{d}} {{\varvec{F}}} {{\varvec{F}}}^{-1}} {{\varvec{F}}} -\frac{1}{3} {\textrm{tr}}({{\varvec{l}}}_{\delta }) {\textrm{d}}{{\varvec{F}}}\right) \end{aligned}$$

(6.9)

$$\begin{aligned}= & {} -\frac{1}{3} J^{-\frac{4}{3}} J ({{\varvec{F}}}^{-T}:{\textrm{d}}{{\varvec{F}}})\left( \delta {{\varvec{F}}}-\frac{1}{3} {\textrm{tr}}({{\varvec{l}}}_{\delta }){{\varvec{F}}}\right) \nonumber \\{} & {} +J^{-\frac{1}{3}} \left( \frac{1}{3} ({{\varvec{l}}}_{\delta }: {{\varvec{l}}}_d^T){{\varvec{F}}} -\frac{1}{3} {\textrm{tr}} ({{\varvec{l}}}_{\delta }) {\textrm{d}}{{\varvec{F}}} \right) \end{aligned}$$

(6.10)

and

$$\begin{aligned}\Rightarrow & {} {\textrm{d}}(\delta \bar{{\varvec{F}}})\bar{{\varvec{F}}}^{-1}= - \frac{1}{3} {\textrm{tr}} ({{\varvec{l}}}_d) \underbrace{\left( {{\varvec{l}}}_{\delta }-\frac{1}{3} {\textrm{tr}} ({{\varvec{l}}}_{\delta }){{\varvec{I}}}\right) }_{{{\varvec{l}}}_{\delta }'}\nonumber \\{} & {} + \frac{1}{3} \left[ ({{\varvec{l}}}_{\delta }:{{\varvec{l}}}_d^T) {{\varvec{I}}} -{\textrm{tr}}({{\varvec{l}}}_{\delta }) {{\varvec{l}}}_d \right] . \end{aligned}$$

(6.11)

Now, incorporating derivatives of $\delta \bar{{\varvec{F}}}$ and $(\delta \bar{{\varvec{F}}})\bar{{\varvec{F}}}^{-1}$ in Eq. 6.8, results:

$$\begin{aligned}\Rightarrow & {} {\textrm{d}}({\varvec{\tau }}_{{\textrm{fic}}}:{{\varvec{d}}}_{\delta }')= {{\varvec{d}}}_{\delta }': \bar{\tiny {\varvec{{\mathbb {C}}}}}^a: {{\varvec{d}}}_{d}' + {{\varvec{l}}}_d' {\varvec{\tau }}_{{\textrm{fic}}}:{{\varvec{l}}}_{\delta }'\nonumber \\{} & {} +{\varvec{\tau }}_{{\textrm{fic}}}: \left( -\frac{1}{3} {\textrm{tr}} ({{\varvec{d}}}_d) {{\varvec{d}}}_{\delta }' + \frac{1}{3} ({{\varvec{l}}}_{\delta }:{{\varvec{l}}}_d^T) {{\varvec{I}}} - \frac{1}{3} {\textrm{tr}} ({{\varvec{l}}}_{\delta }){{\varvec{d}}}_d \right) \end{aligned}$$

(6.12)

$$\begin{aligned}= & {} {{\varvec{d}}}_{\delta }': \bar{\tiny {\varvec{{\mathbb {C}}}}}^a: {{\varvec{d}}}_d'+\left[ {{\varvec{l}}}_d-\frac{1}{3} {\textrm{tr}} ({{\varvec{d}}}_d) {{\varvec{I}}}\right] {\varvec{\tau }}_{{\textrm{fic}}}: \left( {{\varvec{l}}}_{\delta }- \frac{1}{3} {\textrm{tr}} ({{\varvec{d}}}_{\delta }){{\varvec{I}}}\right) \nonumber \\{} & {} -\frac{1}{3} {\textrm{tr}} ({{\varvec{d}}}_d) {\varvec{\tau }}_{{\textrm{fic}}}: {{\varvec{d}}}_{\delta } + \frac{1}{9} {\textrm{tr}} ({{\varvec{d}}}_d) {\textrm{tr}} ({{\varvec{d}}}_{\delta }) {\textrm{tr}} ({\varvec{\tau }}_{\mathrm{{fic}}}) \nonumber \\{} & {} \quad +\frac{1}{3} ({{\varvec{l}}}_{\delta }:{{\varvec{l}}}_d^T) {\textrm{tr}} ({\varvec{\tau }}_{{\textrm{fic}}})-\frac{1}{3} {\textrm{tr}} ({{\varvec{d}}}_{\delta }) {{\varvec{d}}}_d:{\varvec{\tau }}_{{\textrm{fic}}} \nonumber \\{} & {} \quad - \frac{1}{3} {\textrm{tr}} ({\varvec{\tau }}_{{\textrm{fic}}}) {{\varvec{I}}}:{{\varvec{l}}}_d {{\varvec{l}}}_{\delta }^T + \frac{1}{3} {\textrm{tr}} ({\varvec{\tau }}_{{\textrm{fic}}})({{\varvec{l}}}_d: {{\varvec{l}}}_{\delta }) \end{aligned}$$

(6.13)

$$\begin{aligned}= & {} {{\varvec{d}}}_{\delta }': \bar{\tiny {\varvec{{\mathbb {C}}}}}^a: {{\varvec{d}}}_d'+({{\varvec{l}}}_d {\varvec{\tau }}_{{\textrm{fic}}} {{\varvec{l}}}_{\delta }^T):{{\varvec{I}}} \nonumber \\{} & {} -\frac{1}{3} {\textrm{tr}} ({{\varvec{d}}}_{\delta }) {\varvec{\tau }}_{{\textrm{fic}}}: {{\varvec{d}}}_d -\frac{1}{3} {\textrm{tr}} ({{\varvec{d}}}_d) {\varvec{\tau }}_{{\textrm{fic}}}: {{\varvec{d}}}_{\delta } \nonumber \\{} & {} + \frac{1}{9} {\textrm{tr}} ({{\varvec{d}}}_d) {\textrm{tr}} ({{\varvec{d}}}_{\delta }) {\textrm{tr}} ({\varvec{\tau }}_{\mathrm{{fic}}}) \nonumber \\{} & {} -\frac{1}{3} {\textrm{tr}} ({{\varvec{d}}}_d) {\varvec{\tau }}_{{\textrm{fic}}}: {{\varvec{d}}}_{\delta } + \frac{1}{9} {\textrm{tr}} ({{\varvec{d}}}_d) {\textrm{tr}} ({{\varvec{d}}}_{\delta }) {\textrm{tr}} ({\varvec{\tau }}_{\mathrm{{fic}}}) +\frac{1}{3} ({{\varvec{l}}}_{\delta }:{{\varvec{l}}}_d^T) {\textrm{tr}} ({\varvec{\tau }}_{{\textrm{fic}}})\nonumber \\{} & {} -\frac{1}{3} {\textrm{tr}} ({{\varvec{d}}}_{\delta }) {{\varvec{d}}}_d:{\varvec{\tau }}_{{\textrm{fic}}} \underbrace{- \frac{1}{3} {\textrm{tr}} ({\varvec{\tau }}_{{\textrm{fic}}}) {{\varvec{I}}}:{{\varvec{l}}}_d {{\varvec{l}}}_{\delta }^T + \frac{1}{3} {\textrm{tr}} ({\varvec{\tau }}_{{\textrm{fic}}})({{\varvec{l}}}_d: {{\varvec{l}}}_{\delta })}_{0} \end{aligned}$$

(6.14)

$$\begin{aligned}= & {} {{\varvec{d}}}_{\delta }': \bar{\tiny {\varvec{{\mathbb {C}}}}}^a: {{\varvec{d}}}_d' + ({{\varvec{l}}}_d {\varvec{\tau }}_{{\textrm{fic}}}' {{\varvec{l}}}_{\delta }^T):{{\varvec{I}}}\nonumber \\{} & {} - \frac{2}{3} {{\varvec{d}}}_{\delta }: {\varvec{\tau }}_{{\textrm{fic}}} \otimes {{\varvec{I}}}: {{\varvec{d}}}_d + 2.\frac{1}{3} {\textrm{tr}} ({\varvec{\tau }}_{{\textrm{fic}}}) \overbrace{{{\varvec{d}}}_d:{\varvec{{\mathbb {I}}}^s}: {{\varvec{d}}}_{\delta }}^{2.\frac{1}{4}({{\varvec{l}}}_d:{{\varvec{l}}}_{\delta } +{{\varvec{l}}}_d:{{\varvec{l}}}_{\delta }^T)}\nonumber \\{} & {} -\frac{2}{3} {{\varvec{d}}}_{\delta }: {{\varvec{I}}} \otimes {\varvec{\tau }}_{{\textrm{fic}}}: {{\varvec{d}}}_d\nonumber \\{} & {} + \frac{2}{9} {\textrm{tr}}({\varvec{\tau }}_{{\textrm{fic}}}) \text { } {{\varvec{d}}}_{\delta }: {{\varvec{I}}}\otimes {{\varvec{I}}}:{{\varvec{d}}}_d \end{aligned}$$

(6.15)

$$\begin{aligned}= & {} {{\varvec{d}}}_{\delta }': \bar{\tiny {\varvec{{\mathbb {C}}}}}^a: {{\varvec{d}}}_d' + ({{\varvec{l}}}_d {\varvec{\tau }}_{{\textrm{fic}}}' {{\varvec{l}}}_{\delta }^T):{{\varvec{I}}} +{{\varvec{d}}}_{\delta }:\nonumber \\{} & {} \left( -\frac{2}{3} \overbrace{{\varvec{\tau }}_{{\textrm{fic}}}'}^{{\varvec{\tau }}_{\mathrm{{fic}}}-\frac{1}{3} {\textrm{tr}}({\varvec{\tau }}_{\mathrm{{fic}}}) {\varvec{I}}} \otimes {{\varvec{I}}} -\frac{2}{3} {{\varvec{I}}} \otimes {\varvec{\tau }}_{{\textrm{fic}}}' \right) :{{\varvec{d}}}_d \nonumber \\{} & {} - \frac{2}{9} {\textrm{tr}} ({\varvec{\tau }}_{{\textrm{fic}}}) {\textrm{tr}} ({{\varvec{d}}}_d) {\textrm{tr}} ({{\varvec{d}}}_{\delta }) + \frac{2}{3} {\textrm{tr}} ({\varvec{\tau }}_{{\textrm{fic}}}) \text { } {{\varvec{d}}}_{\delta }:{\varvec{{\mathbb {I}}}^s}:{{\varvec{d}}}_d \end{aligned}$$

(6.16)

finally

$$\begin{aligned}{} & {} {\textrm{d}}({\varvec{\tau }}_{{\textrm{fic}}}:{{\varvec{d}}}_{\delta }')= {{\varvec{d}}}_{\delta }:\nonumber \\{} & {} \underbrace{\left( {\varvec{{\mathbb {P}}}}': \bar{\tiny {\varvec{{\mathbb {C}}}}}^a:{\varvec{{\mathbb {P}}}}' -\frac{2}{3} {\varvec{\tau }}_{{\textrm{fic}}}' \otimes {{\varvec{I}}} -\frac{2}{3} {{\varvec{I}}} \otimes {\varvec{\tau }}_{{\textrm{fic}}}'+ \frac{2}{3} {\textrm{tr}} ({\varvec{\tau }}_{{\textrm{fic}}}) {\varvec{{\mathbb {P}}}}'\right) }_{{\varvec{{\mathbb {C}}}}_{{\textrm{iso}}}^a}: {{\varvec{d}}}_d \nonumber \\{} & {} \quad + ({{\varvec{l}}}_d {\varvec{\tau }}_{{\textrm{fic}}}' {{\varvec{l}}}_{\delta }^T): {{\varvec{I}}} \end{aligned}$$

(6.17)

where $\bar{\tiny {\varvec{{\mathbb {C}}}}}^a$ is the fourth order fictitious elasticity tensor and ${\varvec{{\mathbb {P}}}}'$ is the fourth-order deviatoric projector.