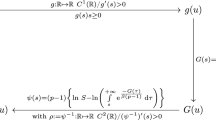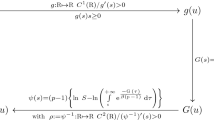Abstract
In this work, we consider parabolic equations of the form
where \(\varepsilon \) is a parameter in \([0,\varepsilon _0)\), and \(\{A_{\varepsilon }(t), \ t\in {\mathbb {R}}\}\) is a family of uniformly sectorial operators. As \(\varepsilon \rightarrow 0^{+}\), we assume that the equation converges to
The time-dependence found on the linear operators \(A_{\varepsilon }(t)\) implies that linear process is the central object to obtain solutions via variation of constants formula. Under suitable conditions on the family \(A_{\varepsilon }(t)\) and on its convergence to \(A_0(t)\) when \(\varepsilon \rightarrow 0^{+}\), we obtain a Trotter-Kato type Approximation Theorem for the linear process \(U_{\varepsilon }(t,\tau )\) associated with \(A_{\varepsilon }(t)\), estimating its convergence to the linear process \(U_0(t,\tau )\) associated with \(A_0(t)\). Through the variation of constants formula and assuming that \(F_{\varepsilon }\) converges to \(F_0\), we analyze how this linear process convergence is transferred to the solution of the semilinear equation. We illustrate the ideas in two examples. First a reaction-diffusion equation in a bounded smooth domain \(\Omega \subset {\mathbb {R}}^{3}\)
where \(a_\varepsilon \) converges to a function \(a_0\), \(f_{\varepsilon }\) converges to \(f_0\). We apply the abstract theory in this example, obtaining convergence of the linear process and solution. As a consequence, we also obtain upper-semicontinuity of the family of pullback attractors associated with each problem. The second example is a nonautonomous strongly damped wave equation
where \(\Delta _D\) is the Laplacian operator with Dirichlet boundary conditions in a domain \(\Omega \) and we analyze convergence of solution as we perturb the fractional powers of the associated linear operator.
Similar content being viewed by others
References
H. Amann, (1995) Linear and Quasilinear Parabolic Problems Vol I. In: Thamil S. (eds.), Monographs in Mathematics, vol. 89. Birkhäuser Boston, Inc., Boston, MA
J.M. Arrieta, Spectral behavior and upper semicontinuity of attractors. In International Conference on Differential Equations, Vol. 1, 2 (Berlin, 1999). World Sci. Publ., River Edge, NJ (2000), 615-621.
J.M. Arrieta, F.D.M. Bezerra, and A.N. Carvalho, Rate of convergence of global attractors of some perturbed reaction-diffusion problems, Topol. Methods Nonlinear Anal. 41 (2) (2013), 229-253.
J.M Arrieta, and A.N. Carvalho, Spectral convergence and nonlinear dynamics of reaction-diffusion equations under perturbations of the domain, J. Differential Equations 199 (1) (2004), 143–178.
J. M. Arrieta, A. N. Carvalho, and A. Rodríguez-Bernal, Parabolic problems with nonlinear boundary conditions and critical nonlinearities, J. Differential Equations 156 (2) (1999), 376–406.
M. Belluzi, T. Caraballo, M.J.D Nascimento, and K. Schiabel, Smoothing effect and asymptotic dynamics of nonautonomous parabolic equations with time-dependent linear operators, J. Differential Equations 314 (2022), 808–849.
F.D.M. Bezerra, A.N. Carvalho, and M.J.D. Nascimento, Fractional approximations of abstract semilinear parabolic problems, Discrete Contin. Dyn. Syst. Ser. B 25 (11) (2020), 4221–4255.
V.L. Carbone, A.N. Carvalho, and K. Schiabel, Continuity of attractors for parabolic problems with localized large diffusion, Nonlinear Anal. 68 (3) (2008), 515–535.
A. N. Carvalho, J. A. Langa, and J. C. Robinson, Attractors for Infinite-dimensional Non-autonomous Dynamical Systems, Applied Mathematical Sciences 182, Springer-Verlag, New York, 2012.
A. N. Carvalho, and M. J. D. Nascimento, Singularly non-autonomous semilinear parabolic problems with critical exponents, Discrete Contin. Dyn. Syst. Ser. S 2 (3) (2009) 449-471.
A.N. Carvalho, and L. Pires, Rate of convergence of attractors for singularly perturbed semilinear problems, J. Math. Anal. Appl. 452 (1) (2017), 258–296.
A.N. Carvalho, and S. Piskarev, A general approximation scheme for attractors of abstract parabolic problems, Numer. Funct. Anal. Optim. 27 (7-8) (2006), 785–829.
J.W. Cholewa, and T. Dlotko, Global attractors in abstract parabolic problems, vol. 278, , Cambridge, 2000.
E.A.M de Abreu, and A.N. Carvalho, (2004) Attractors for semilinear parabolic problems with Dirichlet boundary conditions in varying domains, Mat. Contemp. 27: 37–51.
D. Henry, (1981) Geometric Theory of Semilinear Parabolic Equations, vol. 840, , Berlin-New York.
T. Kato, (1995) Perturbation theory for linear operators. In: Thamil S. (eds.), Classics in Mathematics, Springer, Berlin
F.D.M Bezerra, and M.J.D. Nascimento, (2019) Non-autonomous approximations governed by the fractional powers of damped wave operators, Electron. J. Differential Equations 72: 19.
A. Pazy, Semigroups of Linear Operators and Applications to Partial Differential Equations, Springer-Verlag, New York, 1983.
P.E. Sobolevskiĭ, Equations of parabolic type in a Banach space, Amer. Math. Soc. Transl. 49 (1965), 1-62.
H. Tanabe, A class of the equations of evolution in a Banach space, Osaka Math. J. 11 (1959), 121–145.
H. Tanabe, On the equations of evolution in a Banach space, Osaka Math. J. 12 (1960), 363–376.
H. Tanabe, Remarks on the equations of evolution in a Banach space, Osaka Math. J. 12 (1960), 145–166.
Acknowledgements
The author would like to thank the anonymous referees for the comments and suggestions which improved an earlier version of this work.
Funding
Maykel Boldrin Belluzi has received a research grant from FAPESP, Brazil, process number 2022/01439-5.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The author declares no conflicts of interest. Moreover, data sharing is not applicable to this article as no new data were created or analyzed in this study.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Research supported by FAPESP # 2022/01439-5.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Belluzi, M. Perturbation of parabolic equations with time-dependent linear operators: convergence of linear processes and solutions. J. Evol. Equ. 24, 33 (2024). https://doi.org/10.1007/s00028-024-00961-y
Accepted:
Published:
DOI: https://doi.org/10.1007/s00028-024-00961-y
Keywords
- Nonautonomous parabolic problems
- Time-dependent linear operators
- Perturbed problems
- Convergence of linear process
- Convergence of solutions