Endogeneity in stochastic frontier models with 'wrong' skewness: copula approach without external instruments

Abstract

Stochastic frontier models commonly assume positive skewness for the inefficiency term. However, when this assumption is violated, efficiency scores converge to unity. The potential endogeneity of model regressors introduces another empirical challenge, impeding the identification of causal relationships. This paper tackles these issues by employing an instrument-free estimation method that extends joint estimation through copulas to handle endogenous regressors and skewness issues. The method relies on the Gaussian copula function to capture dependence between endogenous regressors and composite errors with a simultaneous consideration of positively or negatively skewed inefficiency. Model parameters are estimated through maximum likelihood, and Monte Carlo simulations are employed to evaluate the performance of the proposed estimation procedures in finite samples. This research contributes to the stochastic frontier models and production economics literature by presenting a flexible and parsimonious method capable of addressing wrong skewness of inefficiency and endogenous regressors simultaneously. The applicability of the method is demonstrated through an empirical example.

1 Introduction

The classical assumption in stochastic frontier (SF) production models is that inefficiency exhibits positive skewness, resulting in the composite error, i.e., the regression residuals, having negative skewness. However, in empirical applications, the residuals may exhibit positive skewness, which contradicts the assumption of positively skewed inefficiency. Waldman (1982) first demonstrated that if the residuals from the SF model have ‘wrong’ skewness, i.e., positive, inefficiency variance is biased towards zero. Consequently, efficiency scores tend to be one, leading to false conclusions of high efficiency (Hafner et al. 2018). Green and Mayes (1991) argue that this either indicates ‘super efficiency’ (all firms in the industry operate close to the frontier) or the inappropriateness of the SF analysis technique to measure inefficiencies. Thus, implausibly high efficiency scores obtained under the classical SF specification can indicate misspecification of inefficiency skewness (Haschka and Wied 2022).

Another significant empirical challenge arises in the case of regressor endogeneity. Endogeneity can be loosely defined as dependence between regressors and errors, which is particularly important for SF models, as this dependence may stem from inefficiency, idiosyncratic noise, or both (Tran and Tsionas 2015). Linking endogenous covariate information with composite errors can lead to biased estimates for causal effects if the methods used assume regressor exogeneity (Haschka and Herwartz 2022, 2020). The standard approach to handling the endogeneity problem in SF models is to use likelihood-based instrumental variable (IV) estimation methods (Amsler et al. 2016; Kutlu 2010; Prokhorov et al. 2020; Tran and Tsionas 2013). However, a general drawback of such methods is their reliance on the availability of external information to construct instruments. Instruments, if available at all, are often subject to potential pitfalls if they fail to adequately meet the two required conditions: they must be sufficiently correlated with the endogenous regressors and uncorrelated with the composite errors term. Thus, a potential difficulty in implementing IV-based estimators arises when there is no external information available to construct appropriate instruments (Haschka et al. 2020).

Given that suitable instrumental information in SF models is often scant, unavailable, or weak, this study proposes an SF model with a data-driven choice of correct or wrong skewness, which we conceptualize as an extension of the IV-free joint estimation model using copulas introduced by Park and Gupta (2012). Copula techniques have been successfully adopted for classical SF models (Tran and Tsionas 2015), and we extend them to address cases of wrong skewness. The method relies on a copula function to directly model dependencies between endogenous regressors and composite errors, thus eliminating the need for external information. Specifically, copulas allow for the separate modeling of marginal distributions of endogenous regressors and composite errors, while capturing their dependency. We construct the joint distribution of the endogenous regressor and composite error, which accommodates mutual dependency between them. Subsequently, we use this joint distribution to derive the likelihood function, which distinguishes between correct and wrong skewness through an indicator function, and maximize it to obtain consistent estimates of model parameters.

The empirical analysis aims to impartially explore the determinants of firm performance based on data from 16,641 Vietnamese firms in 2015. A key observation is that the presence of wrong skewness is compounded by endogeneity, while the suggested estimator provides an unbiased perspective. The empirical findings indicating wrong skewness imply a growing number of inefficient firms persisting in the market, challenging the assumption of a competitive landscape. This persistence in inefficiency is likely influenced by factors such as corruption and the constraints imposed by the communist regime, hindering the establishment of liberal and competitive market conditions. Consequently, policy interventions are deemed necessary to incentivize firms to optimize their processes and improve efficiency.

The paper is organized as follows. Section 2 presents the model and discusses the copula approach to deal with regressor endogeneity in SF models with wrong skewness. In Sect. 3, we examine the finite sample performance of the proposed approach through Monte Carlo simulations. An empirical application is provided in Sect. 4. We revisit the methodology in Sects. 5, and  6 concludes with a summary of our contribution.

2 Methodology

Consider the standard SF model given by:

$$\begin{aligned} y_{i} = x_{i}^{\prime } \beta + z_{i}^{\prime } \delta + \underbrace{v_{i} - u_{i}}_{e_{i}}, \quad i = 1, \ldots , n, \end{aligned}$$

(1)

Here, $y_{i}$ represents the output of producer i, $x_{i}$ is an $L \times 1$ vector of exogenous inputs, $z_{i}$ is a $K \times 1$ vector of endogenous inputs, $\beta$ and $\delta$ are $L \times 1$ and $K \times 1$ vectors of unknown parameters to be estimated, respectively. Additionally, $v_i$ is a symmetric random error, $u_i$ is a one-sided random disturbance representing technical efficiency, and the composite error is denoted as $e_{i} = v_{i} - u_{i}$. It is assumed that $x_{i}$ is uncorrelated with $e_{i}$, while $z_{i}$ is allowed to be correlated with $e_{i}$, giving rise to endogeneity, but we make no assumption regarding the source of endogeneity, being it correlation with $v_{i}$ or with $u_{i}$. Furthermore, it is assumed that $u_{i}$ and $v_{i}$ are independent, and the skewness of $u_{i}$ is left unrestricted. This discussion can be readily extended to cases where the (exogenous) environmental variables are included in the distribution of $u_{i}$ (Battese and Coelli 1995; Haschka and Herwartz 2022).

2.1 ‘Wrong’ skewness of inefficiency distribution

Adhering to standard SF practices, we presume that $v_{i} \sim {\textrm{N}}(0, \sigma _{v}^2)$ represents symmetric, two-sided idiosyncratic noise. In this context, our model operates under the assumption that skewness issues arise from the inefficiency term, while $v_{i}$ itself is symmetric.¹ Following the approach of Hafner et al. (2018), we delineate two cases for $u_{i}$ that characterise the distributional shape:

$$\begin{aligned}&\text{`Correct' skewness:} \nonumber \\&\quad \quad \quad u_{i} \sim N_{[0, \infty )}(0, \gamma ^{2}), \quad \gamma > 0 \end{aligned}$$

(2)

$$\begin{aligned}&\text{`Wrong' skewness:} \nonumber \\&\quad \quad \quad u_{i}\sim N_{[0, a_{0}|\gamma |)}(a_{0}|\gamma |, \gamma ^{2}), \quad \gamma < 0 \end{aligned}$$

(3)

The assumption in (2) is widely acknowledged, characterising the correct skewness of $u_{i}$ (and consequently $e_{i}$) due to the strictly decreasing density of $u_{i}$ in the interval $[0, \infty )$ (Kumbhakar and Lovell 2003), and constitutes the classical SF model. On the contrary, wrong skewness is induced by (3), where $a_{0} \approx 1.389$ represents the non-trivial solution of $\frac{\phi (0)}{\Phi (0)} = a_{0}+\frac{\phi \left( a_{0}\right) -\phi (0)}{\Phi \left( a_{0}\right) -\Phi (0)}$, and the density of $u_{i}$ is strictly increasing and bounded in $[0, a_{0}|\gamma |]$.

It is noteworthy that the expectations of both $u_{i}$ and $e_{i}$ remain unaffected by the skewness’ sign (Hafner et al. 2018). Thus, the inefficiency variance and the sign of skewness are directly linked because $\gamma > 0$ ($\gamma < 0$) induces correct (wrong) skewness, but $\mathbb {E}[u_{i}]$ and $\mathbb {E}[e_{i}]$ are not influenced by the sign of $\gamma$. By convolution of v with u and integration, the density of $e_{i} = v_{i} - u_{i}$ obtains as:

$$\begin{aligned}&\text{`Correct' skewness:} \nonumber \\&\quad \quad \quad g_{e}^{+}(e) =\frac{2}{\sigma }\phi \left( \frac{e}{\sigma } \right) \Phi \left( - \frac{e \gamma }{\sigma \sigma _v} \right) , \end{aligned}$$

(4)

$$\begin{aligned}&\text{`Wrong' skewness:} \nonumber \\&\quad \quad \quad g_{e}^{-}(e) =\frac{1}{\sigma \left( \Phi \left( a_{0}\right) -\Phi (0)\right) } \phi \left( \frac{e-a_{0} \gamma }{\sigma }\right) \left[ \Phi \left( A_{w}+\frac{a_{0} \sigma }{\sigma _{v}}\right) -\Phi \left( A_{w}\right) \right] , \nonumber \\&\quad \qquad A_{w} =\frac{e-a_{0} \gamma }{\sigma } \frac{\gamma }{\sigma _{v}}, \end{aligned}$$

(5)

with $\sigma ^2 = \gamma ^2 + \sigma _{v}^{2}$ and $\int e g_{e}^{+}(e) \ de = \int e g_{e}^{-}(e) \ de$. It is important to note that under correct skewness, e follows a (1x1)-dimensional closed skew normal (CSN) distribution, denoted as $e^{+} \sim CSN(0, \sigma ^{2}, -\frac{\gamma }{\sigma _{v}\sigma }, 0, 1)$, while, as demonstrated by Haschka and Wied (2022), under wrong skewness, e follows a (1x2)-dimensional CSN distribution, denoted as $e^{-} \sim CSN_{1\times 2}\left( a_{0}\gamma , \sigma ^{2}, \left( \begin{array}{c} \gamma /\sigma \\ -\gamma /\sigma \end{array}\right) , \left( \begin{array}{c} -a_{0}\sigma \\ 0 \end{array}\right) , \left( \begin{array}{cc} \sigma ^{2}_{v} &{} 0 \\ 0 &{} \sigma ^{2}_{v} \end{array}\right) \right)$. Consequently, it becomes evident that another advantage of the distribution in (3) is its association with the well-known CSN distribution. As a result, properties of the CSN distribution, such as moments, can be derived (Flecher et al. 2009).

Although Li (1996) argues that one-sided distributions with an unbounded range always exhibit positive skewness, Johnson et al. (1995) demonstrates that the two-parameter Weibull distribution can have both positive and (small) negative skewness for specific parameter combinations. Accordingly, this distribution could be an alternative without needing to impose an upper boundary. However, since the upper bound of the distribution in (3) depends on $\gamma$, the advantage of using the truncated normal distribution in (3) is that it entails negative skewness without necessitating the identification of additional parameters. Moreover, other parsimonious distributions for u that can produce wrong skewness, such as the negative skew-exponential distribution discussed in Hafner et al. (2018), may also be considered. However, in such cases, it would not be clear if the distribution of e will be known or has a closed-form expression.

Fig. 1

Densities of u and e for $\gamma = 2.5$, i.e., correct skewness (dotted lines) and $\gamma = -2.5$, i.e., wrong skewness (solid lines); with $\sigma _{v} =.5$

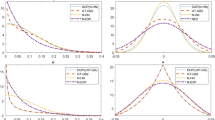
The configuration of the inefficiency distribution under both correct and wrong skewness is illustrated in Panel (a) of Fig. 1, with the corresponding distributions of composite errors presented in Panel (b). When $\gamma > 0$, the distribution of u exhibits positive skewness, while the distribution of e has negative skewness. Conversely, for $\gamma < 0$, the skewness of u becomes negative, and that of e is positive. It is important to emphasize that the adopted one-sided distribution for inefficiency, which can result in both correct and wrong skewness, is parsimonious. Alternative approaches allowing for a data-driven selection of either correct or wrong skewness often involve identifying multiple parameters determining the inefficiency distribution (see, e.g., Tsionas 2017, for Weibull inefficiency), may not result in a well-known distribution for composite errors, or require a priori determination of the skewness sign (corrected OLS or modified OLS). However, such determinations are challenging in the presence of endogeneity.

2.2 Joint estimation using copulas

Consider $F(z_{1}, \ldots , z_{K}, e)$ and $f(z_{1}, \ldots , z_{K}, e)$ as the joint distribution and joint density of endogenous regressors $(z_{1}, \ldots , z_{K})$ and composite errors e, respectively. In practical applications, $F(\cdot )$ and $f(\cdot )$ are unknown due to the unobservability of e and thus require estimation. In line with the methodology proposed by Park and Gupta (2012), we employ a copula approach to approximate this joint density. The copula serves as a tool to capture dependence within the joint distribution of endogenous regressors and composite errors.

Let $\varvec{\omega }_{z,i} = (F_{z1}(z_{1i}), \ldots , F_{zK}(z_{Ki}) )^{\prime }$ and $\omega _{e,i} = G(e_{i}; \sigma _{v}, \gamma )$ represent the margins $(\varvec{\omega }_{z,i}, \omega _{e,i})^{\prime } \in [0,1]^{K+1}$ based on a probability integral transform. Here, the F’s signify the respective marginal cumulative distribution functions of the observed endogenous regressors, and $G(e_{i}; \sigma _{v}, \gamma )$ is the cumulative distribution function of the CSN distribution for errors, subject to the sign of $\gamma$. Drawing on the approach by Haschka (2021) and Tran and Tsionas (2015), we substitute $F _ { 1 } \left( z _ { 1i } \right) , \ldots , F _ { p } \left( z _ { pi } \right)$ with their respective empirical counterparts in a first stage. Given observed samples of $z_{ji}$, $j=1, \dots , p$; $i=1, \dots , n$, we utilise the empirical cumulative distribution function (ecdf) of $z_{j}$, denoted as $\hat{F}_{j} = \frac{ 1 }{ n + 1 } \sum _ { i = 1 } ^ {n} \mathbbm {1} \left( z _ { j i } \le z _ { 0 j } \right)$.

Utilising a Gaussian copula, $\hat{\varvec{\xi }}_{z,i} = (\Phi ^{-1}(\hat{F}_{z1}(z_{1i})), \ldots , \Phi ^{-1}(\hat{F}_{zK}(z{Ki})) )^{\prime }$, and $\hat{\xi }_{e,i} = \Phi ^{-1}(G(\hat{e}_{i}; \hat{\sigma }_{v},\hat{\gamma }))$, both follow a standard multivariate normal distribution with a dimension of $(K+1)$ and a correlation matrix $\Xi$. Subsequently, the joint density can be expressed as

$$\begin{aligned} f( \varvec{z}_{i}, e_{i}) =&\frac{1}{\sqrt{\det ( \Xi )}} \exp \left( -\frac{1}{2}\left( \begin{array}{c} \hat{\varvec{\xi }}_{z,i} \\ \hat{\xi }_{e,i} \end{array}\right) ^{\prime }\left( \Xi ^{-1}-I\right) \left( \begin{array}{c} \hat{\varvec{\xi }}_{z,i} \\ \hat{\xi }_{e,i} \end{array}\right) \right) \nonumber \\&\times g ( e_{i}; \sigma _{v}, \gamma ) \times \prod _ { k = 1 } ^ { K } f _ { zk } \left( \check{z} _ { ki } \right) , \end{aligned}$$

(6)

where $\xi _{e,i}$ and $g ( e_{i}; \sigma _{v}, \gamma )$ are again subject to either correct or wrong skewness. The copula density in the first row establishes a connection between the error and all endogenous variables. Meanwhile, the densities in the second row describe the marginal behaviour. The marginal densities $f _ { zk } \left( \check{z} _ { ki } \right)$ in (6) do not involve any parameters of interest and can be omitted when deriving the likelihood since they function as normalising constants.

To simultaneously determine the choice of correct or wrong skewness based on the sign of $\gamma$, we adopt the approach of Hafner et al. (2018) and incorporate an indicator function into the likelihood. While Hafner et al. (2018) propose choosing correct or wrong skewness a priori by examining the skewness of the OLS residual, our method estimates the sign of $\gamma$ simultaneously with all other parameters. This is preferred because any pre-determination of residual skewness could be influenced by (potential) endogeneity. Consequently, the likelihood function is given by:

$$\begin{aligned}&L(\varvec{\theta } \mid y,\varvec{z},\varvec{x}) \ \propto \ \mathbbm {1} (\gamma > 0) \prod _{i=1}^{n} \ \frac{1}{\sqrt{\det ( \Xi )}} \nonumber \\&\quad \exp \left( -\frac{1}{2}\left( \begin{array}{c} \hat{\varvec{\xi }}_{z,i} \\ \hat{\xi }^{+}_{e,i} \end{array}\right) ^{\prime }\left( \Xi ^{-1}-I\right) \left( \begin{array}{c} \hat{\varvec{\xi }}_{z,i} \\ \hat{\xi }^{+}_{e,i} \end{array}\right) \right) g^{+} ( e_{i}; \sigma _{v}, \gamma ) \nonumber \\&\quad + \mathbbm {1} (\gamma < 0) \prod _{i=1}^{n} \ \frac{1}{\sqrt{\det ( \Xi )}} \exp \left( -\frac{1}{2}\left( \begin{array}{c} \hat{\varvec{\xi }}_{z,i} \\ \hat{\xi }^{-}_{e,i} \end{array}\right) ^{\prime }\left( \Xi ^{-1}-I\right) \left( \begin{array}{c} \hat{\varvec{\xi }}_{z,i} \\ \hat{\xi }^{-}_{e,i} \end{array}\right) \right) g^{-} ( e_{i}; \sigma _{v}, \gamma ) \nonumber \\&\quad + \mathbbm {1} (\gamma = 0) \prod _{i=1}^{n} \ \frac{1}{\sqrt{\det ( \Xi )}} \exp \left( -\frac{1}{2}\left( \begin{array}{c} \hat{\varvec{\xi }}_{z,i} \\ \hat{\xi }^{0}_{e,i} \end{array}\right) ^{\prime }\left( \Xi ^{-1}-I\right) \left( \begin{array}{c} \hat{\varvec{\xi }}_{z,i} \\ \hat{\xi }^{0}_{e,i} \end{array}\right) \right) \phi ( e_{i}; \sigma _{v}). \end{aligned}$$

(7)

To explicitly account for the scenario of only fully efficient firms, the likelihood also accommodates $\gamma = 0$.² In this case, the marginal distribution of the errors follows a normal distribution with mean zero and variance $\sigma _{v}^2$, represented as $\xi ^{0}_{e,i} = e_{i} / \sigma _{v}$. Notably, our approach encompasses those of Hafner et al. (2018), Tran and Tsionas (2015), and Park and Gupta (2012). Specifically, under the assumption of exogeneity of all regressors ($\Xi = I$), the likelihood in (7) reduces to that in Hafner et al. (2018). In the case of correct skewness ($\gamma > 0$), corresponding to the traditional SF model, the likelihood collapses to that in Tran and Tsionas (2015). Finally, for the scenario of only fully efficient firms ($\gamma = 0$), it reduces to that in Park and Gupta (2012). Subsequently, the likelihood is logarithms and maximised with respect to the vector of unknown parameters $\varvec{\theta } = (\beta , \delta , \sigma ^{2}{v}, \gamma , \text{vechl}[\Xi ])$, where $\text{vechl}[\Xi ] = (\rho _{1}, \ldots , \rho _{K})^{\prime }$ stacks the lower diagonal elements of the correlation matrix $\Xi$ into a column vector.

With parameter estimates, technical inefficiency $u_i$ can be predicted using Jondrow et al. (1982) as follows:

$$\begin{aligned}&\text{`Correct' skewness:} \nonumber \\&\quad \hat{u}_i =\hat{E}\left( u_i \mid e_i\right) =\frac{\sqrt{\hat{\gamma }^2 + \hat{\sigma }_{v}^{2}} (\hat{\gamma } / \hat{\sigma }_{v})}{1+(\hat{\gamma } / \hat{\sigma }_{v})^2}\left[ \frac{\phi \left( (\hat{\gamma } / \hat{\sigma }_{v}) \hat{e}_i / \sqrt{\hat{\gamma } + \hat{\sigma }_{v})}\right) }{1-\Phi \left( (\hat{\gamma } / \hat{\sigma }_{v}) \hat{e}_i / \sqrt{\hat{\gamma } + \hat{\sigma }_{v})}\right) }\right. \nonumber \\&\qquad \left. -\frac{(\hat{\gamma } / \hat{\sigma }_{v}) \hat{e}_i}{\sqrt{\hat{\gamma }^2 + \hat{\sigma }_{v}^{2})}}\right] \end{aligned}$$

(8)

$$\begin{aligned}&\text{`Wrong' skewness:} \nonumber \\&\quad \hat{u}_i =\hat{E}\left( u_i \mid e_i\right) = \int _{0}^{a_{0}|\hat{\gamma }|} \exp \{-u_{i} \} f^{-}(u_{i} \mid e_{i} ) du_{i} \end{aligned}$$

(9)

Note that in the case of correct skewness, the predicted technical inefficiency has a closed-form expression, while under wrong skewness, the integral needs to be solved numerically (Hafner et al. 2018).

2.2.1 Model identifiability

In our framework, model identification hinges on two key conditions: (i) the distribution of endogenous regressors must differ from that of the composite error (for an in-depth discussion on identification in copula-based endogeneity-correction models, see Haschka 2022b; Papadopoulos 2022; Park and Gupta 2012). Consequently, the model maintains identification as long as $\gamma$ is not zero (or very close to zero), and endogenous regressors deviate from a normal distribution. However, identification collapses if $\gamma = 0$ (resulting in a normal composite error, in which case our model aligns with that of Park and Gupta 2012), and endogenous regressors follow a normal distribution. In such a scenario, the joint distribution of endogenous regressors and the composite error becomes multivariate normal, implying a linear relationship between the endogenous regressors and the composite error. Consequently, we would be unable to distinguish the linear effect of the endogenous regressor on the outcome. To address this, a formal separation of $\mathbb {E}[y | z]$ from $\mathbb {E}[e | z]$ without IV information is impossible if both are linear functions, as indicated by joint normality (Haschka 2022b).

In contrast, when the joint distribution is not multivariate normal (with $\gamma = 0$, indicating the non-normality of endogenous regressors), the relationship between regressors and errors becomes non-linear. Identification in this context does not require IVs and can be accomplished through the joint distribution of e and z. Although $\mathbb {E}[y | z]$ remains a linear function due to the specification of a linear regression model, non-normality implies that $\mathbb {E}[e | z]$ becomes a non-linear function. This non-linearity facilitates the separation of variation attributed to endogenous regressors from the variation due to the composite error, as discussed in Tran and Tsionas (2015). Consequently, in empirical applications, it is essential to assess the marginal distribution of endogenous regressors before estimation-an approach commonly adopted in empirical literature utilizing copula-based identification (e.g., Haschka 2022b; Papadopoulos 2022; Park and Gupta 2012).

Through the utilization of a Gaussian copula, model identification also requires (ii) a linear dependence between $\varvec{\xi }{z}$ and $\xi {e}$, enabling the correlation to be expressed through pairwise Pearson coefficients. Consequently, the model exclusively accommodates (iii) continuous endogenous regressors (or discrete with numerous distinct outcomes). In instances where $z_{k}$ is continuous, $\xi _{z, k} = (\Phi ^{-1}(F_{zk}(z_{k})))$ follows a standard normal distribution. Conversely, if $z_{k}$ is binary, $\xi _{z, k}$ would also be binary, and multivariate normality with $\xi _{e}$ would not be guaranteed. While the continuity of $z_{k}$ is crucial and its verification is straightforward, confirming the assumption of Gaussian-type dependence is more challenging empirically due to the unobservability of errors. However, since any copula capable of modeling multivariate dependency structures can be employed, this identification assumption can be readily substituted when opting for a different copula. Despite this, in cases where the true dependence deviates from the Gaussian copula assumption, existing literature has demonstrated the robustness of the Gaussian copula in flexibly capturing various non-Gaussian dependencies (Becker et al. 2021; Haschka 2022b; Park and Gupta 2012). Papadopoulos (2022) suggest testing for the multivariate normality of $\varvec{\xi }_{z}$ to assess the suitability of the Gaussian copula, allowing for the determination of whether the assumption holds for a specific part of the model. Nevertheless, given the Gaussian copula’s robustness in modeling diverse dependency structures, significance in this context does not necessarily imply adverse effects on model identification.

2.2.2 Bootstrap inference and asymptotic behaviour

Copula-based endogeneity-correction models are commonly formulated as two-step estimation approaches, with the marginal cumulative distribution function of endogenous regressors determined a priori through a data-driven process.³ In the initial stage, we derive the margins $\hat{\varvec{\omega }}_{z,i}$, representing the probability integral transformed endogenous variables through the empirical cumulative distribution function. This serves as an estimator for the cumulative distribution function (CDF) (Joe and Xu 1996). In the subsequent step, these estimated margins are incorporated into the likelihood function in (7) as plug-in estimates. This introduces two significant implications for the estimator in the second stage. Firstly, the estimator cannot achieve unbiasedness since estimated CDFs from the sample are used instead of those from the population (Genest et al. 1995). Therefore, it is crucial to establish consistency, a validation that will be undertaken through Monte Carlo simulations. Secondly, standard errors in the second stage are generally unreliable as uncertainties from the first stage are not taken into account.

The employed copula estimator can be categorized as a semiparametric method since it combines the nonparametric distribution of endogenous regressors from the first stage with the parametric CSN distribution of the composite errors and the parametric Gaussian copula constituting the likelihood in the second stage (Genest et al. 1995). In semiparametric models, deriving Hessian-based asymptotic standard errors can be notably challenging, making bootstrap procedures a natural alternative for evaluating estimation uncertainty (Haschka and Herwartz 2022; Park and Gupta 2012). Consequently, we employ bootstrapping to derive standard errors and confidence intervals.

Recently, Breitung et al. (2023) argued that it remains uncertain a priori whether the standard properties of maximum likelihood (ML) estimation hold for IV-free copula-based endogeneity corrections and under which assumptions they may be applicable. The challenge of formulating precise statements about limiting properties in the presence of a nonparametrically generated regressor is a highly intricate task. This challenge is inherent in all copula-based approaches that rely on the joint estimation of errors and endogenous regressors with a priori estimated cumulative distribution functions (Haschka 2022b; Park and Gupta 2012; Tran and Tsionas 2015). Nevertheless, Papadopoulos (2022) and Tran and Tsionas (2015) conjectured that such estimators exhibit consistency and asymptotic normality in stochastic frontier (SF) settings (for additional simulation-based evidence on asymptotic behavior, see Haschka 2022b; Haschka and Herwartz 2022). Although specific consistency (i.e., robustness) theory for quasi-maximum likelihood estimation (quasi-MLE) for Gaussian copula-based models exists (Prokhorov and Schmidt 2009), it is unclear whether these results are valid in the case of generated regressors. However, some insights from related literature (Breitung et al. 2023; Genest et al. 1995) can be applied. Under exogeneity, the generated regressors do not impact the asymptotic distributions, and the estimator asymptotically follows a standard normal distribution (Breitung et al. 2023). In the case of endogeneity, the limiting distribution is unknown. As demonstrated by Breitung et al. (2023) for linear regression models with Gaussian outcomes (i.e., no SF specifications), the asymptotic distribution depends on unknown parameters (under endogeneity). In this context, we assume that in the case of an SF specification (non-zero $\gamma$), the asymptotic distribution differs from that derived in Breitung et al. (2023) - more precisely, it depends on other unknown parameters. Consequently, no general theoretical statement can be made about the asymptotic behavior of the estimator.

3 Monte Carlo simulations

To assess the finite sample performance of the proposed copula estimator, we conduct Monte Carlo simulations based on the following data generating process (DGP):

$$\begin{aligned} y_{i}&= \beta x_{i} + \delta z_{i} + v_{i} - u_{i} \end{aligned}$$

(10)

$$\begin{aligned} z_{i}&= \alpha s_{i} + \eta _{i} \end{aligned}$$

(11)

$$\begin{aligned} u_{i}&\sim \left\{ \begin{array}{ll} {\textrm{N}}_{[0, \infty )}(0, \gamma ^{2}) &{}\quad \text{if} \ \gamma > 0, \\ {\textrm{N}}_{[0, a_{0}|\gamma |]}(a_{0}|\gamma |, \gamma ^{2}) &{} \quad \text{if} \ \gamma < 0, \end{array}\right. \end{aligned}$$

(12)

In (12), positive (negative) values of $\gamma$ result in the distribution of $u_{it}$ having positive (negative) skewness, with both distributions having the same expectation. The random variables $x_{i}$ and $s_{i}$ are each generated independently as $\chi ^{2}(2)$. To introduce endogeneity, the vector of errors $(v_{i}, \eta _{i})^{\prime }$ is generated by:

$$\begin{aligned} \left( \begin{array}{c}{v_{i}} \\ {\eta _{i}}\end{array}\right) \sim {\textrm{N}}\left( \left[ \begin{array}{l}{0} \\ {0}\end{array}\right] ,\left[ \begin{array}{ll}{1} &{} {\rho } \\ {\rho } &{} {1}\end{array}\right] \right) . \end{aligned}$$

(13)

In our experiments, we fix $\alpha = \beta = \delta =.5$ and rescale $v_{i} = v_{i}/2$ to achieve a signal-to-noise ratio of $\gamma / \sigma _{v} = 2$, which is common is assessing performance of SF models in Monte Carlo simulations (see e.g., Chen et al. 2014; Haschka and Wied 2022). To assess scenarios under exogeneity and endogeneity, we set $\rho = \{ 0,.35,.7 \}$. While the scenario with exogeneity is intended to highlight the costs of accounting for endogeneity, introducing endogeneity in a stepwise manner allows monitoring how the performance is affected. We further distinguish $\gamma = \{-1, 1 \}$ to introduce either negative or positive skewness. Finally, the sample size is $N = 750$, and each experiment is replicated 1000 times. For comparison purposes, we also compute the Maximum Likelihood Estimator (MLE) by Hafner et al. (2018), which considers correct and wrong skewness but does not account for endogeneity, an instrument-based Generalised Method of Moments (GMM) estimator (Tran and Tsionas 2013), and an IV-free copula estimator (Tran and Tsionas 2015), both of which address endogenous regressors but assume correctly skewed inefficiency.

Estimation results for scenarios of exogeneity and endogeneity with either correct or wrong skewness are shown in Table 1. When the skewness of the inefficiency distribution is correctly specified (upper panel) and the regressors are exogenous, all estimators are unbiased. In this scenario, ML is the method of choice as it yields the smallest standard deviations, while the remaining approaches (GMM, copula, proposed) are characterized by higher uncertainty as they unnecessarily allow for endogeneity. This scenario thus highlights the costs of incorrectly accounting for endogeneity.

Table 1 Monte Carlo simulation results are presented for simulations based on the DGP in Eqs. (10) to (13) under scenarios of exogeneity ($\rho = 0$) and endogeneity ($\rho = {.35,.7}$), considering both correct skewness ($\gamma > 1$, upper panel) and wrong skewness ($\gamma < 0$, lower panel)

Under moderate endogeneity ($\rho =.35$), ML deteriorates and exhibits bias for all model parameters. This bias becomes even more pronounced when endogeneity becomes stronger ($\rho =.7$). While GMM, copula, and the proposed estimator perform equally well and remain unbiased regardless of the degree of endogeneity, estimates obtained by GMM are most tightly centered around true values, primarily because it is IV-based and access to valid instruments strongly benefits efficiency (for similar findings, see Tran and Tsionas 2015).

Misspecifying the skewness of the inefficiency distribution (lower panel) has particularly detrimental effects on the GMM and copula estimators. Even in the absence of endogeneity, both estimators yield biased slope coefficients. Misspecification of the error distribution due to wrong skewness is falsely attributed to endogeneity, leading to biased estimates (for further simulation-based evidence, see Haschka and Herwartz 2022). Consequently, efficiency scores are also biased. When introducing endogeneity, GMM and copula remain biased due to misspecified error distribution.

Moreover, the ML estimator yields an incorrect sign of skewness when the true inefficiency exhibits wrong skewness. While the ML estimator is capable of detecting wrong skewness under exogeneity, it fails to do so under endogeneity. Specifically, even with moderate endogeneity ($\rho =.35$), if the true coefficient is $\gamma = -1$, the ML estimator yields a coefficient estimate of .1892, incorrectly suggesting correct skewness. This highlights a substantial hindrance in detecting wrong skewness in the presence of endogenous regressors. By contrast, the proposed approach remains generally unaffected, is unbiased for all coefficients, and provides accurate assessments of efficiency.

4 Application

We demonstrate the practicality of the proposed approach through an empirical analysis, assessing firm efficiency using data from Vietnamese firms in the year 2015 obtained from the Vietnam Enterprise Survey (VES). The VES, conducted annually by the General Statistics Office (GSO) of Vietnam, is a nationally representative survey encompassing all firms with 30 or more employees, along with a representative sample of smaller firms (O’Toole and Newman 2017). Our evaluation of firm performance follows established approaches in the literature, examining the interplay between firm revenue, wages, and assets (e.g., Haschka et al. 2021, 2023). Descriptive statistics for the involved variables are presented in Table 2.

Table 2 Summary Statistics: All variables are measured in million Vietnamese Dong

By treating each firm as an individual producer, we adopt a log-linear Cobb–Douglas production function and specify the following model:

$$\begin{aligned} \log revenue_{i} = \alpha + \delta _{1} \log wages_{i} + \delta _{2} \log assets_{i} + v_{i} - u_{i}, \end{aligned}$$

(14)

where $i = 1, \ldots , 16,474$ represents firms, and $v_{i} \sim {\textrm{N}}(0, \sigma _{v}^2)$ is idiosyncratic noise. Our specification differs from related models in the following two aspects. First, we allow stochastic inefficiency to vary across i and consider both correct and wrong skewness by employing a data-driven choice of the distribution of $u_i$, i.e.:

$$\begin{aligned} u_{i} \sim {\textrm{N}}_{[0, \infty )}(0, \gamma ^{2}) \quad \text{or} \quad u_{i} \sim {\textrm{N}}_{[0, a_{0}|\gamma |]}(a_{0}|\gamma |, \gamma ^{2}). \end{aligned}$$

(15)

The latter case has not been explored in the empirical development literature, providing a novel perspective to uncover structural inefficiencies in firm performance in Vietnam. Although we label it as a ’data-driven choice’, the sign of $\gamma$ is not estimated a priori but is determined simultaneously with all other parameters (note that we also allow for $\gamma = 0$). This approach is adopted because any predetermination of residual skewness could be influenced by potential endogeneity. In this context, we examine the possibility of correlated production inputs with composed errors, denoted as $e_i = v_i - u_i$. Endogeneity of inputs can arise due to their correlation with $v_i$, with $u_i$, or both. The presence of omitted variables in the production function, such as subsidies or governmental grants that have substantial effects, may lead to correlation with $v_i$. Furthermore, if producers possess prior knowledge of potential inefficiencies in output generation, they are likely to adjust their inputs accordingly (Haschka and Herwartz 2022). As these adjustments are unobserved by the analyst, they introduce correlation with $u_i$.

We conduct a comparative analysis of the proposed estimator, which accommodates endogeneity of inputs and considers both correct and wrong skewness of inefficiency, with the alternative estimators considered in the Monte Carlo simulations. These are ML (Hafner et al. 2018), copula (Tran and Tsionas 2015), and GMM (Tran and Tsionas 2013). To set up the IV-based GMM estimator, we employ one-year lagged assets and one-year lagged wages as instruments, following a similar approach used in previous studies (Haschka and Herwartz 2022). However, it is important to note that such internal instrumentation may suffer from weak instruments and might not be entirely suitable for handling endogeneity.

Table 3 Estimation outcomes are presented employing MLE (Hafner et al. 2018), GMM (Tran and Tsionas 2013), copula-based estimation (Tran and Tsionas 2015), and our proposed estimator. Standard errors for copula-based estimators (copula and proposed) are determined through bootstrap procedures with 1,999 replications. Efficiency scores are computed utilising the estimator by Jondrow et al. (1982)

Table 3 presents the estimation results, which consistently indicate human capital as the primary driver of firm performance in Vietnam across all employed estimators. This is evident from the significantly higher coefficient associated with log wages compared to log assets. The consideration of endogeneity through GMM, Copula, and the proposed estimator reduces the observed difference in coefficients. GMM and Copula estimators may still face remaining endogeneity issues when wrong skewness is present, with GMM encountering additional challenges due to potential weak instrumentation. MLE indicates increasing returns to scale, as reflected in the sum of the elasticities associated with wages and assets being above one. However, for Copula and GMM, this sum significantly falls below one, suggesting decreasing returns to scale. This implies that scaling up is challenging for firms. By contrast, the proposed estimator yields constant returns to scale, which aligns with the dataset dominated by small firms (O’Toole and Newman 2017).

The discrepancy raises concerns about the MLE results being flawed due to endogeneity. Further evidence supporting endogeneity is found in the significant estimates of correlations between production inputs and errors when using Copula and the proposed estimators. In terms of firm efficiency, MLE yields surprisingly high mean efficiency, with an average score of .7280. However, accounting for endogeneity while assuming correct skewness through GMM and Copula estimators decreases mean efficiency scores to .4169 (GMM) and .3903 (Copula). The proposed approach reveals a mean efficiency of .6126. While GMM and Copula estimators exhibit minimal differences among all coefficients, the results undergo significant changes when the proposed estimator is applied. Notably, the proposed estimator indicates the presence of wrong skewness after accounting for endogeneity, which is challenging for MLE to detect under such conditions.

The insights derived from the proposed estimator contribute evidence supporting the existence of endogenous regressors and wrong skewness. While the former has been previously emphasized in empirical development literature, the latter has not received recognition. To comprehend the economic reasons and market mechanisms behind the occurrence of wrong skewness, it is crucial to delve into the contributing factors. As illustrated in Panel (a) of Fig. 1, the presence of correct skewness (dotted line) indicates that most firms should operate near the efficiency frontier, aligning with competitive market conditions where inefficient firms are likely to exit due to a lack of competitiveness. Conversely, empirical evidence supporting wrong skewness (straight line) implies a growing number of inefficient firms persisting in the market, contradicting the assumption of a competitive market situation. This suggests a lack of incentives for firms to optimize efficiency, attributed to factors such as widespread corruption and the constraints imposed by the communist regime in Vietnam. Despite ongoing reforms, these challenges persist, necessitating policy interventions to incentivize firms to optimize processes and improve efficiency, as market forces alone seem insufficient to generate such incentives.

5 Discussion of the methodology

The proposed approach offers several advantages that make it useful for handling both endogeneity and skewness issues. Firstly, it overcomes the need for instrumental variables, eliminating the challenge of obtaining and validating such instruments. By employing a copula function to directly connect endogenous regressors and errors, the model exhibits parsimony and requires the identification of only one additional parameter for each endogenous regressor - the correlation coefficient depicting regressor-error dependence. This parsimony is further bolstered by the one-parameter inefficiency distribution, which can accommodate both correct and wrong skewness with only one parameter to estimate. The sign of this parameter determines the skewness. Additionally, the likelihood function is readily obtained even under wrong skewness, as the errors follow a CSN distribution for which certain properties can be derived (Flecher et al. 2009). This simplifies the estimation process and enhances the model’s computational efficiency.

The proposed approach does have certain limitations, which stem from either the SF specifications or the copula function employed for endogeneity correction. On the one hand, while we attribute wrong skewness to the inefficiency component, other potential sources, such as asymmetry in idiosyncratic noise or dependence between idiosyncratic noise and inefficiency, could also be responsible. Additionally, we restrict our attention to the (truncated) half-normal distribution for inefficiency. While this choice simplifies the analysis by ensuring a CSN distribution after convolution with the normal distribution assumed for idiosyncratic noise, alternative distributions for inefficiency could be considered, such as the negative skew exponential distribution (Hafner et al. 2018). While the choice of appropriate distribution assumptions is a key consideration in any SF model, in the context of wrong skewness, we would also need to establish whether the density of $e = v - u$, resulting from the convolution of v with u, follows a known parametric distribution.

On the other hand, while the Gaussian copula exhibits considerable flexibility, particularly when dealing with multiple endogenous regressors as in the empirical application, it is rooted in the assumption of linear dependency between its margins. However, prior studies have demonstrated the robustness of the Gaussian copula in capturing various non-Gaussian dependencies (Haschka 2022b; Haschka and Herwartz 2022; Park and Gupta 2012). By virtue, any copula-based endogeneity correction generally disregards the potential sources of endogeneity, be it omitted variables, reverse causality, or simultaneity, as they are employed to address the symptoms of endogeneity. Regarding the SF specification, it is further complicated by the fact of discerning whether endogeneity arises from correlation with the inefficiency term or idiosyncratic noise because we model the joint distribution of endogenous regressors and composite errors. Moreover, the proposed approach only allows for continuous endogenous variables. Since model identification necessitates marginal distributions of endogenous regressors to be different from that of the composite errors (which follow a CSN distribution), empirical applications demand an a priori assessment of the marginal distribution of explanatory variables. For instance, in cases where the model incorporates only fully efficient firms, the endogenous regressors must exhibit a non-normal distribution.

While instrumental variable estimation remains the preferred method for addressing endogeneity when strong and valid instruments are available, weak instrumentation or skewness misspecifications pose empirical challenges to such fully parametric approaches. Nevertheless, we expect that the proposed method offers valuable alternatives for numerous empirical SF models that encounter regressor endogeneity and/or skewness issues.

6 Conclusion

Traditional stochastic frontier (SF) models typically assume that inefficiency follows a half-normal distribution with positive skewness. However, when true inefficiency exhibits negative skewness, efficiency scores are biased toward one, leading to misleading conclusions of high efficiency (Waldman 1982). While recent literature has highlighted the importance of addressing the ’wrong’ skewness problem in SF analysis (Curtiss et al. 2021; Choi et al. 2021; Daniel et al. 2019), existing studies have not considered the potential endogeneity of regressors. This paper fills this gap by proposing an instrument-free approach for estimating SF models with endogenous regressors and allowing for a simultaneous choice of inefficiency skewness.

Building upon the work of Park and Gupta (2012), we employ a copula function to directly construct the joint density of endogenous regressors and composite errors, enabling us to capture mutual dependency without the need for instrumental variables. Our model distinguishes between correct and wrong skewness without imposing a priori restrictions on the sign of inefficiency skewness or requiring the identification of additional parameters governing its direction. We evaluate the finite sample performance of the approach through Monte Carlo simulations. The simulation results demonstrate that the estimator performs well in finite samples, exhibiting desirable properties in terms of bias and mean squared error. These findings are further validated in an empirical application.

The following contributions of this article are also worth mentioning. On the methodological front, we advance the understanding of copula-based endogeneity corrections in scenarios with non-Gaussian outcomes. Joint estimation using copulas still occupies a niche in endogeneity-robust modeling (Papies et al. 2023; Papadopoulos 2021). Our work contributes to bridging this gap by understanding copula-based endogeneity corrections in SF settings.

The existing methodological literature about dealing with skewness issues in SF models predominantly addresses the symptoms but fails to delve into the underlying causes, often attributing skewness issues to weak samples (Almanidis and Sickles 2011; Hafner et al. 2018; Simar and Wilson 2009). Empirically, Papadopoulos and Parmeter (2023) note that only two studies in the past 25 years have considered skewness issues in SF analyses. However, these studies remain silent on the potential economic explanations for skewness. Our study breaks new ground by attributing skewness to the inefficiency component of the SF model, providing an economic explanation for this phenomenon.

Regarding the empirical application, this study is the first to explicitly address and account for skewness issues when applying SF models in a development economics context. Previous studies on firm growth in Vietnam using SF analysis, such as Haschka et al. (2023), have overlooked potential skewness issues in their findings. By incorporating an economic explanation for wrong skewness and proposing an endogeneity-robust methodology, we offer a novel perspective on growth dynamics in Vietnam and shed light on underlying competition levels.