Periodic solution problems of neutral-type stochastic neural networks with time-varying delays

Zheng, Famei; Li, Xiaoliang; Du, Bo

doi:10.3389/fphy.2024.1338799

ORIGINAL RESEARCH article

Front. Phys., 05 April 2024
Sec. Mathematical Physics
Volume 12 - 2024 | https://doi.org/10.3389/fphy.2024.1338799

Periodic solution problems of neutral-type stochastic neural networks with time-varying delays

Famei Zheng¹

Xiaoliang Li²*

Bo Du¹*

¹School of Mathematics and Statistics, Huaiyin Normal University, Huaian, Jiangsu, China
²Jiyang College, Zhejiang Agriculture and Forestry University, Zhuji, Zhejiang, China

This paper is devoted to investigating a class of stochastic neutral-type neural networks with delays. By using the fixed point theorem and the properties of neutral-type operator, we obtain the existence conditions for periodic solutions of stochastic neutral-type neural networks. Furthermore, we obtain the conditions for the exponential stability of periodic solutions using Gronwall-Bellman inequality and stochastic analysis technique. Finally, a numerical example is given to show the effectiveness and merits of the present results. Our results can be used to obtain the existence and exponential stability of periodic solution to the corresponding deterministic systems.

1 Introduction

During the past years, the theory of stochastic differential equations has been extensively studied, see, e.g., [1–5] and references therein. However, periodic solution problems of stochastic differential equations have been studied by few authors. To be best our knowledge, we only find that very few results for periodic solution of stochastic differential equations and stochastic differential systems have been obtained. In [6], Kolmanovskii and Myshkis introduced basic theory of T − periodic stochastic process and T − periodic solution for stochastic retard differential equation which greatly promoted the study of periodic solutions of stochastic differential equations. It $\hat{o}$ and Nisio [7] studied stationary solutions of a stochastic differential equation. Has’minskii [8] studied the existence of periodic solution of differential equations with random right sides. In [9], the authors considered existence problems for periodic Markov process and stochastic functional differential equations by using the properties of periodic Markov processes. After that, Li and Xu [10] also obtained the existence of periodic solution for a stochastic functional differential equation with unbounded delays. In [11], Zhang and Gopalsamy considered two classes of n − species stochastic population models with periodic coefficients and obtained some sufficient conditions for the existence of a stochastically asymptotically stable in the large periodic solution process. In [12], the authors studied mean-square almost periodic solution for impulsive stochastic by applying Cauchy matrix. Jiang, etc. [13, 14] dealt with periodic solution of nonautonomous logistic equation with random perturbation.

In the real world, a specific neural network is always affected by various uncertain factors, stochastic perturbations are almost inevitable [15]. Therefore, it is necessary to investigate effects of stochastic perturbations on the dynamic properties of neural networks. Recent years, stochastic neural networks has been extensively studied. Stability analysis of various stochastic neural networks see, e.g., [16–19]. In [16], the authors considered the distributed synchronization of coupled neural networks. Zhu and Cao [17, 18] investigated exponential stability of stochastic neural networks with both Markovian jump parameters and mixed time delays. Stability analysis of switched stochastic neural networks with time-varying delays has been studied in [19]. The stability and stabilization for a class of stochastic systems with impulsive effects, see [20]; the pth moment (p ≥ 2) and the almost-sure stability of stochastic Cohen-Grossberg neural networks, see [21]; stochastic neural networks with local impulsive effects, see [22]. For deterministic neural network, see, e.g., [23, 24]. However, there are not many achievements in the study of periodic solutions of stochastic neural networks. Using fixed points principle and Gronwall-Bellman inequality, the authors [25] concerned with the periodic solutions for a class of stochastic Cohen-Grossberg neural networks with time-varying delays. Yang and Li [26] considered existence and exponential stability of periodic solution for stochastic Hopfield neural networks on time scales. Wang and Wu [27] studied mean square exponential stability and periodic solutions of stochastic interval neural networks with mixed time delays. For recent advances in periodic solution of stochastic differential equation and neural networks, see [28–34].

Our main purpose of this paper is to study periodic solution of a stochastic neutral-type neural networks by using the contraction mapping theorem and Gronwall-Bellman inequality. For First, an effective existence and uniqueness theorem of periodic solution for considered system is established. Then, some sufficient conditions for the exponential stability of periodic solution are given. Because the system we study contains neutral terms and random perturbations, it is difficult to obtain the existence conditions of periodic solutions. To overcome the above difficulties, as one will see, several novel mathematic analysis methods are applied. These existence and stability theorems are rather general and therefore have great power in applications.

The distinctive contributions of this paper are outlined as follows:

(1) It is noted that most existing results on stochastic neural networks are mainly pertaining to the stability of considered systems, see e.g., [9–11] and related references. In this paper, we obtained existence results of periodic solution by using the contraction mapping theorem. Hence, the research content of this article expands the scope of research on nonlinear neutral stochastic differential systems.

(2) We develop some techniques of stochastic analysis for studying stochastic neutral-type neural networks with delays, our methods for the proof of main results can more easily be understood. Particularly, we use contraction mapping theorem and Gronwall-Bellman inequality for obtaining stability results which is different from ones in [14–16, 35–37].

(3) Our main results are also valid for the case of the corresponding deterministic systems.

The following sections are organized as follows: In Section 2, we introduce some useful Lemmas and Definitions. In Section 3, some sufficient conditions are established for existence and uniqueness of periodic solution of the considered system. Section 4 gives some sufficient conditions for guaranteeing the exponential stability of periodic solution. In Section 5, an example is given to show the feasibility of our results. Finally, some conclusions are given for this paper.

2 Preliminaries

In the present paper, we consider a stochastic neutral-type neural networks with delays of the form

\begin{aligned} d [x_{i} (t) - c_{i} (t) x_{i} (t - γ)] & = [[- a_{i} (t) x_{i} (t) + \sum_{j = 1}^{n} a_{i j} (t) f_{j} (x_{j} (t)) + \sum_{j = 1}^{n} d_{i j} (t) g_{j} (x_{j} (t - τ_{i j} (t))) + I_{i} (t)]] d t \\ + \sum_{j = 1}^{n} σ_{i j} (x_{j} (t)) d ξ_{j} (t), i = 1,2, \dots, n, \end{aligned} (2.1)

where n is the number of units in the considered system, γ > 0 is a delay, x_i(t) is the state of the ith neuron at time t, f_j(⋅) and g_j(⋅) are the activation functions of the jth unit, a_i(t) ≥ 0 denotes the rate with which the ith unit will reset its potential to the resting state in isolation when disconnected from the networks and external inputs, a_ij(t) and d_ij(t) denote the strength of the jth neuron on ith unit at time t and t − τ_ij(t), respectively, I_i(t) denotes the ith component of an external input source, $ξ (t) = {(ξ_{1} (t), \dots, ξ_{n} (t))}^{⊤}$ is the standard Wiener process defined on complete probability space $(Ω, F, {F_{t}}_{t > 0}, P)$ σ_ij is Borel measurable function. We assume that c_i(t), τ_ij(t), a_i(t), a_ij(t), d_ij(t) and I_j(t) are defined on $R$ , are T − periodic and continuous functions. The initial condition of Eq. 2.1 is

x_{i} (s) = ϕ_{i} (s), s \in (- \infty, t_{0}], (2.2)

where $ϕ_{i} (s) \in C ((- \infty, t_{0}], R), t_{0} \in R$ .

Let B be a Banach space with the norm ‖ ⋅‖ and $L^{p} (P, B) (p \geq 1)$ be the space of all B-value random variable X such that $E (‖ x ‖^{p}) = \int_{Ω} ‖ x ‖^{p} d P$ . Let f(x) be a continuous T − peridic function on $R$ . Denote

\bar{f} = \max_{x \in R} | f (x) |, \underset{̲}{f} = \min_{x \in R} | f (x) | .

Throughout this paper, we assume that.

(H₁) $f_{j}, g_{j}, σ_{i j} \in C (R, R)$ are Lipschitz-continuous with Lipschitz constants $L_{j}^{f}, L_{j}^{g}$ and l_ij, respectively, i, j = 1, 2, … , n.

( $H_{1}^{'}$ ) $f_{j}, g_{j} \in C (R, R)$ are Lipschitz-continuous with Lipschitz constants $L_{j}^{f}$ and $L_{j}^{g}$ , respectively, j = 1, 2, … , n.

Definition 2.1. [8] A stochastic process x_t(s) is said to be periodic with period T if its finite dimensional distributions are periodic with period T, that is, for any positive integer n and any moments of time t₁, t₂, … , t_n the joint distribution of the random variables $x_{t_{1} + k T} (s), x_{t_{2} + k T} (s), \dots, x_{t_{n} + k T} (s)$ are independent of $k, k \in Z$ .

Remark 2.1. [8] If x(t) is an T − periodic stochastic process, then its mathematical expectation and variance are T − periodic.

Lemma 2.1. [5] (The It $\hat{o}$ isometry) If f(t, ω) is is bounded and elementary, then

E [{(\int_{a}^{b} f (t, ω) d B_{t} (ω))}^{2}] = E (\int_{a}^{b} f^{2} (t, ω) d t) .

Lemma 2.2. [38] For each $x \in R_{+}^{n}$ and p > 0,

| x |^{p} \leq n^{(\frac{p}{2} - 1) \lor 0} \sum_{i = 1}^{n} x_{i}^{p}, {(\sum_{i = 1}^{n} x_{i})}^{p} \leq n^{(p - 1) \lor 0} \sum_{i = 1}^{n} x_{i}^{p},

where ∨ denotes the Min operator, that is,

a \lor b = \{\begin{matrix} a for a \leq b, \\ b for a > b . \end{matrix}

Lemma 2.3. [39] Let

A : C_{T} \to C_{T}, [A x] (t) = x (t) - c (t) x (t - τ), \forall t \in R .

If |c(t)| ≠ 1, then operator A has continuous inverse A⁻¹ on C_T, satisfying.

[A^{- 1} f] (t) = \{\begin{matrix} f (t) + \sum_{j = 1}^{\infty} \prod_{i = 1}^{j} c (t - (i - 1) τ) f (t - j τ), c_{0} < 1, \forall f \in C_{T}, \\ - \frac{f (t + τ)}{c (t + τ)} - \sum_{j = 1}^{\infty} \prod_{i = 1}^{j + 1} \frac{1}{c (t + i τ)} f (t + j τ + τ), σ > 1, \forall f \in C_{T}, \end{matrix}

\int_{0}^{T} | [A^{- 1} f] (t) | d t \leq \{\begin{matrix} \frac{1}{1 - c_{0}} \int_{0}^{T} | f (t) | d t, c_{0} < 1, \forall f \in C_{T}, \\ \frac{1}{σ - 1} \int_{0}^{T} | f (t) | d t, σ > 1, \forall f \in C_{T}, \end{matrix}

| A^{- 1} f |_{0} \leq \{\begin{matrix} \frac{1}{1 - c_{0}} | f |_{0}, c_{0} < 1, \forall f \in C_{T}, \\ \frac{1}{σ - 1} | f |_{0}, σ > 1, \forall f \in C_{T} . \end{matrix},

where $c_{0} = \max_{t \in {[0, ω]}_{T}} | c (t) |, σ = \min_{t \in {[0, ω]}_{T}} | c (t) |, C_{T} = {x : x \in C (R, R), x (t + T) \equiv x (t)}$ .

Remark 2.2. From Lemma 2.3, we have

| A^{- 1} f |_{0} \leq c^{*} | f |_{0},

where $c^{*} = \max {\frac{1}{1 - c_{0}}, \frac{1}{σ - 1}}$ .

Definition 2.2. [25] The periodic solution x(t, t₀, ϕ) with initial value ϕ of system (2.1) is said to be globally exponentially stable, if there are constants λ > 0 and M > 1 such that for any solution y(t, t₀, ϕ₁) with initial value ϕ₁ of system (2.1) satisfies

E (‖ x - y ‖^{2}) \leq M E (‖ ϕ - ϕ_{1} ‖^{2}) e^{- λ (t - t_{0})}, t \geq t_{0} .

Let (A_ix_i) (t) = x_i(t) − c_i(t)x_i(t − γ) = y_i(t). From Lemma 2.3, then $x_{i} (t) = (A_{i}^{- 1} y_{i}) (t)$ , and system (2.1) can be rewritten by

\begin{aligned} d y_{i} (t) & = [- a_{i} (t) y_{i} (t) - a_{i} (t) c_{i} (t) (A_{i}^{- 1} y_{i}) (t - γ) + \sum_{j = 1}^{n} a_{i j} (t) f_{j} ((A_{j}^{- 1} y_{j}) (t)) \\ + \sum_{j = 1}^{n} d_{i j} (t) g_{j} ((A_{j}^{- 1} y_{j}) (t - τ_{i j} (t))) + I_{i} (t)] d t + \sum_{j = 1}^{n} σ_{i j} ((A_{j}^{- 1} y_{j}) (t)) d ξ_{j} (t), i = 1,2, \dots, n, \end{aligned} (2.3)

with initial condition

y_{i} (s) = A_{i} ϕ_{i} (s) = ψ_{i} (s), s \in (- \infty, t_{0}] . (2.4)

Remark 2.3. system (2.1) is equivalent to system (2.3). Thus, system (2.1) has a globally exponentially stable periodic solution, if and only if, system (2.3) has a globally exponentially stable periodic solution. Since system (2.3) has not neutral-type term, we can easily obtain existence and stability results for system (2.3).

Remark 2.4. System (2.1) is a neutral-type stochastic system which shows the neutral properties by D − operator x_i(t) − c_i(t)x_i(t − γ). For the details about D − operator, see [40]. Some results of stochastic system with D − operator have been obtained, see [41–43] and related references. However, there exist few results for the periodic solution of stochastic system with D − operator. This paper is devoted to investigating the above problem and obtaining the new results.

3 Existence of periodic solution

In this section, we will show the existence of periodic solutions for system (2.1). Now, consider the linear section for system (2.3)

y_{i}^{'} (t) = - a_{i} (t) y_{i} (t) . (3.1)

By basic theory for ordinary differential equation, system (3.1) has a solution

y_{i} (t) = G_{i} (t, t_{0}) y_{i} (t_{0}), i = 1,2, \dots, n,

where $G_{i} (t, t_{0}) = e^{- \int_{t_{0}}^{t} a_{i} (s) d s}$ . It is easy to see that

G_{i} (t, t_{0}) \leq e^{- \underset{̲}{a_{i}} (t - t_{0})} f o r t \geq t_{0}, i = 1,2, \dots, n . (3.2)

Theorem 3.1. Suppose that |c_i(t)| ≠ 1, i = 1, 2, … , n and assumption (H₁) holds. Then system (2.1) has unique T-periodic solution, provided that

δ = \max_{1 \leq i \leq n} \{\frac{2 Λ_{i}}{{\underset{̲}{a_{i}}}^{2}}\} < 1, (3.3)

where

Λ_{i} = {(c_{i}^{*} {\bar{a}}_{i} {\bar{c}}_{i} + \sum_{j = 1}^{n} ({\bar{a}}_{i j} L_{j}^{f} c_{j}^{*} + {\bar{d}}_{i j} L_{j}^{g} c_{j}^{*}))}^{2} + {(\sum_{j = 1}^{n} l_{i j} c_{j}^{*})}^{2},

c_{i}^{*} = \max \{\frac{1}{1 - {\bar{c}}_{i}}, \frac{1}{\underset{̲}{c_{i}} - 1}\} .

Proof. Let

X = \{x = {(x_{1}, x_{2}, \dots, x_{n})}^{T} \in C (R, R^{n}) : x_{i} (t + T) = x_{i} (t), i = 1,2, \dots, n\}

with the norm $‖ x ‖_{X} = E | x |_{1}^{2}$ , where $| x |_{1} = \max_{1 \leq i \leq n} \sup_{t \in R} | x_{i} (t) |$ . Then $X$ is a Banach space. Define a map Γ on $X$ by

(Γ ϕ) (t) = {({(Γ ϕ)}_{1} (t), {(Γ ϕ)}_{2} (t), \dots, {(Γ ϕ)}_{n} (t))}^{T}, t \in R,

where

\begin{aligned} {(Γ ϕ)}_{i} (t) & = \int_{- \infty}^{t} G_{i} (t, s) [- a_{i} (s) c_{i} (s) (A_{i}^{- 1} y_{i}) (s - γ) + \sum_{j = 1}^{n} a_{i j} (s) f_{j} ((A_{j}^{- 1} y_{j}) (s)) \\ + \sum_{j = 1}^{n} d_{i j} (s) g_{j} ((A_{j}^{- 1} y_{j}) (s - τ_{i j} (s))) + I_{i} (s)] d s \\ + \int_{- \infty}^{t} G_{i} (t, s) \sum_{j = 1}^{n} σ_{i j} ((A_{j}^{- 1} y_{j}) (s)) d ξ_{j} (s), i = 1,2, \dots, n . \end{aligned}

Obviously, (Γϕ)_i(t + T) = (Γϕ)_i(t). Hence, Γ maps $X$ to $X$ . Next, we show that Γ is a contraction mapping. For any $u, v \in X$ , we have

\begin{aligned} | {(Γ u)}_{i} (t) - {(Γ v)}_{i} (t) | & = |\int_{- \infty}^{t} G_{i} (t, s) [- a_{i} (s) c_{i} (s) [(A_{i}^{- 1} u_{i}) (s - γ) - (A_{i}^{- 1} v_{i}) (s - γ)] \\ + \sum_{j = 1}^{n} a_{i j} (s) [f_{j} ((A_{j}^{- 1} u_{j}) (s)) - f_{j} ((A_{j}^{- 1} v_{j}) (s))] \\ + \sum_{j = 1}^{n} d_{i j} (s) [g_{j} ((A_{j}^{- 1} u_{j}) (s - τ_{i j} (s))) - g_{j} ((A_{j}^{- 1} v_{j}) (s - τ_{i j} (s)))]] d s \\ + \int_{- \infty}^{t} G_{i} (t, s) \sum_{j = 1}^{n} [σ_{i j} ((A_{j}^{- 1} u_{j}) (s)) - σ_{i j} ((A_{j}^{- 1} v_{j}) (s))] d ξ_{j} (s)| . \end{aligned} (3.4)

For i = 1, 2, … , n, let

\begin{aligned} F_{1 i} & = \int_{- \infty}^{t} G_{i} (t, s) [- a_{i} (s) c_{i} (s) [(A_{i}^{- 1} u_{i}) (s - γ) - (A_{i}^{- 1} v_{i}) (s - γ)] \\ + \sum_{j = 1}^{n} a_{i j} (s) [f_{j} ((A_{j}^{- 1} u_{j}) (s)) - f_{j} ((A_{j}^{- 1} v_{j}) (s))] \\ + \sum_{j = 1}^{n} d_{i j} (s) [g_{j} ((A_{j}^{- 1} u_{j}) (s - τ_{i j} (s))) - g_{j} ((A_{j}^{- 1} v_{j}) (s - τ_{i j} (s)))]] d s \end{aligned}

and

F_{2 i} = \int_{- \infty}^{t} G_{i} (t, s) \sum_{j = 1}^{n} [σ_{i j} ((A_{j}^{- 1} u_{j}) (s)) - σ_{i j} ((A_{j}^{- 1} v_{j}) (s))] d ξ_{j} (s) .

Taking expectations for the above F_1i and F_2i, by Lemma 2.2, we have

E {|{(Γ u)}_{i} (t) - {(Γ v)}_{i} (t)|}^{2} \leq 2 E (| F_{1 i} |^{2} + | F_{2 i} |^{2}), i = 1,2, \dots, n . (3.5)

Evaluating the first term of the right-hand side of (3.5), in view of Lemma 2.3, (3.2) and assumption (H₁), we have

\begin{aligned} E | F_{1 i} |^{2} & = E |\int_{- \infty}^{t} G_{i} (t, s) [- a_{i} (s) c_{i} (s) [(A_{i}^{- 1} u_{i}) (s - γ) - (A_{i}^{- 1} v_{i}) (s - γ)] \\ + \sum_{j = 1}^{n} a_{i j} (s) [f_{j} ((A_{j}^{- 1} u_{j}) (s)) - f_{j} ((A_{j}^{- 1} v_{j}) (s))] \\ {+ \sum_{j = 1}^{n} d_{i j} (s) [g_{j} ((A_{j}^{- 1} u_{j}) (s - τ_{i j} (s))) - g_{j} ((A_{j}^{- 1} v_{j}) (s - τ_{i j} (s)))]] d s|}^{2} \\ \leq {[\frac{1}{\underset{̲}{a_{i}}} (c_{i}^{*} {\bar{a}}_{i} {\bar{c}}_{i} + \sum_{j = 1}^{n} ({\bar{a}}_{i j} L_{j}^{f} c_{j}^{*} + {\bar{d}}_{i j} L_{j}^{g} c_{j}^{*}))]}^{2} E | u - v |_{1}^{2} . \end{aligned} (3.6)

As to the second term of the right-hand side of (3.5), in view of Lemma 2.1, Lemma 2.3, (3.2) and assumption (H₁), we also have

\begin{aligned} E | F_{2 i} |^{2} & = E {|\int_{- \infty}^{t} G_{i} (t, s) \sum_{j = 1}^{n} [σ_{i j} ((A_{j}^{- 1} u_{j}) (s)) - σ_{i j} ((A_{j}^{- 1} v_{j}) (s))] d ξ_{j} (s)|}^{2} \\ = E |\int_{- \infty}^{t} {|G_{i} (t, s) \sum_{j = 1}^{n} [σ_{i j} ((A_{j}^{- 1} u_{j}) (s)) - σ_{i j} ((A_{j}^{- 1} v_{j}) (s))]|}^{2} d s| \\ \leq {[\frac{1}{\underset{̲}{a_{i}}} \sum_{j = 1}^{n} l_{i j} c_{j}^{*}]}^{2} E | u - v |_{1}^{2} . \end{aligned} (3.7)

From (3.5-3.7), we have

\begin{aligned} E | Γ u - Γ v |_{1}^{2} & \leq 2 [{(\frac{1}{\underset{̲}{a_{i}}} (c_{i}^{*} {\bar{a}}_{i} {\bar{c}}_{i} + \sum_{j = 1}^{n} ({\bar{a}}_{i j} L_{j}^{f} c_{j}^{*} + {\bar{d}}_{i j} L_{j}^{g} c_{j}^{*})))}^{2} + {(\frac{1}{\underset{̲}{a_{i}}} \sum_{j = 1}^{n} l_{i j} c_{j}^{*})}^{2}] E | u - v |_{1}^{2} \\ = 2 \frac{1}{{\underset{̲}{a_{i}}}^{2}} Λ_{i} E | u - v |_{1}^{2} \\ \leq δ E | u - v |_{1}^{2} . \end{aligned}

Thus,

‖ Γ u - Γ v ‖_{X} \leq δ ‖ u - v ‖_{X} .

By (3.1) Γ is a contraction mapping on $X$ system (2.3) has a unique periodic solution y_i(t), i.e., system (2.1) has a unique periodic solution $x_{i} (t) = (A_{i}^{- 1} y_{i}) (t), i = 1,2, \dots, n$ .

Remark 3.1. Consider the corresponding deterministic system of system (2.1)

d [x_{i} (t) - c_{i} (t) x_{i} (t - γ)] = [- a_{i} (t) x_{i} (t) + \sum_{j = 1}^{n} a_{i j} (t) f_{j} (x_{j} (t)) + \sum_{j = 1}^{n} d_{i j} (t) g_{j} (x_{j} (t - τ_{i j} (t))) + I_{i} (t)]] d t, (3.8)

where i = 1, 2, … , n.

Corollary 3.1. Suppose that |c_i(t)| ≠ 1, i = 1, 2, … , n and assumption ( $H_{1}^{'}$ ) holds. Then system (3.8) has unique T-periodic solution, provided that

\tilde{δ} = \max_{1 \leq i \leq n} \{\frac{2 {\tilde{Λ}}_{i}}{{\underset{̲}{a_{i}}}^{2}}\} < 1,

where

{\tilde{Λ}}_{i} = {(c_{i}^{*} {\bar{a}}_{i} {\bar{c}}_{i} + \sum_{j = 1}^{n} ({\bar{a}}_{i j} L_{j}^{f} c_{j}^{*} + {\bar{d}}_{i j} L_{j}^{g} c_{j}^{*}))}^{2},

c_{i}^{*} = \max \{\frac{1}{1 - {\bar{c}}_{i}}, \frac{1}{\underset{̲}{c_{i}} - 1}\} .

Remark 3.2. To the best of our knowledge, few authors deal with the existence and exponential stability of periodic solutions to stochastic neutral-type neural networks by using contraction mapping theorem and Gronwall-Bellman inequality. Most articles only studied the stability of stochastic neural networks, and the results on the existence of solutions are not many, see e.g., [17–19, 21, 22]. Therefore, the results of this article enrich and develop the research content and methods of stochastic neural networks. It should be pointed out that the properties of regarding neutral-type operators in Lemma 2.3 have important applications for obtaining the main results of this paper. I believe that the above properties of neutral-type operators will have wide applications in studying other types of neutral-type systems.

Remark 3.3. In [44], the authors studied periodic solution problem of a class of stochastic nonlinear system with delays; in this paper, we investigated periodic solution problem of a class of stochastic neutral-type neural networks with delays. The above two systems are obviously different. Furthermore The main research methods in [44] are stochastic analysis technique and Lyaplov functional method, see Theorem 2.2, Lemma 2.3 and Lemma 2.4 in [44]; the main research methods in this paper are contraction mapping theorem and Gronwall-Bellman inequality which are different from the corresponding ones in [44].

4 Globally exponential stability of periodic solution

In this section, we firstly show the exponential stability of periodic solutions for system (2.3) with initial condition (2.4). Then, we further obtain the exponential stability of periodic solutions for system (2.1) with initial condition (2.2).

Theorem 4.1. Suppose that all conditions of Theorem 3.1 hold. Then, the periodic solution of system (2.1) is globally exponentially stable, provided that

λ = \min_{1 \leq i \leq n} \{2 \underset{̲}{a_{i}} - Λ_{i}\} > 0 and 3 {(c_{i}^{*})}^{2} > 1, i = 1,2, \dots, n . (4.1)

Proof. From Theorem 3.1, system (2.3) has a periodic solution y_i(t) with initial condition ψ_i(s), where i = 1, 2, … , n, s ∈ (−∞, t₀]. Assume that $y_{i}^{*} (t)$ is an arbitrary solution of system (2.3) with the initial condition $ψ_{i}^{*} (s)$ , where i = 1, 2, … , n, s ∈ (−∞, t₀]. From basic theory of ordinary differential equation, system (2.3) has a solution

\begin{aligned} y_{i} (t) & = G_{i} (t, t_{0}) y_{i} (t_{0}) + \int_{t_{0}}^{t} G_{i} (t, s) [- a_{i} (s) c_{i} (s) (A_{i}^{- 1} y_{i}) (s - γ) + \sum_{j = 1}^{n} a_{i j} (s) f_{j} ((A_{j}^{- 1} y_{j}) (s)) \\ + \sum_{j = 1}^{n} d_{i j} (s) g_{j} ((A_{j}^{- 1} y_{j}) (s - τ_{i j} (s))) + I_{i} (s)]] d s \\ + \int_{t_{0}}^{t} G_{i} (t, s) \sum_{j = 1}^{n} σ_{i j} ((A_{j}^{- 1} y_{j}) (s)) d ξ_{j} (s), \end{aligned} (4.2)

where i = 1, 2, … , n, t ≥ t₀. Let $z_{i} (t) = y_{i} (t) - y_{i}^{*} (t)$ . By (4.2), we have

\begin{aligned} z_{i} (t) & = z_{i} (t_{0}) G_{i} (t, t_{0}) + \int_{t_{0}}^{t} G_{i} (t, s) [- a_{i} (s) c_{i} (s) [(A_{i}^{- 1} y_{i}) (s - γ) - (A_{i}^{- 1} y_{i}^{*}) (s - γ)] \\ + \sum_{j = 1}^{n} a_{i j} (s) [f_{j} ((A_{j}^{- 1} y_{j}) (s)) - f_{j} ((A_{j}^{- 1} y_{j}^{*}) (s))] \\ + \sum_{j = 1}^{n} d_{i j} (s) [g_{j} ((A_{j}^{- 1} y_{j}) (s - τ_{i j} (s))) - g_{j} ((A_{j}^{- 1} y_{j}^{*}) (s - τ_{i j} (s)))]]] d s \\ + \int_{t_{0}}^{t} G_{i} (t, s) \sum_{j = 1}^{n} [σ_{i j} ((A_{j}^{- 1} y_{j}) (s)) - σ_{i j} ((A_{j}^{- 1} y_{j}^{*}) (s))] d ξ_{j} (s) . \end{aligned} (4.3)

Let

H_{1 i} = z_{i} (t_{0}) G_{i} (t, t_{0}),

\begin{aligned} H_{2 i} & = \int_{t_{0}}^{t} G_{i} (t, s) [- a_{i} (s) c_{i} (s) [(A_{i}^{- 1} y_{i}) (s - γ) - (A_{i}^{- 1} y_{i}^{*}) (s - γ)] \\ + \sum_{j = 1}^{n} a_{i j} (s) [f_{j} ((A_{j}^{- 1} y_{j}) (s)) - f_{j} ((A_{j}^{- 1} y_{j}^{*}) (s))] \\ + \sum_{j = 1}^{n} d_{i j} (s) [g_{j} ((A_{j}^{- 1} y_{j}) (s - τ_{i j} (s))) - g_{j} ((A_{j}^{- 1} y_{j}^{*}) (s - τ_{i j} (s)))]]] d s, \end{aligned}

H_{3 i} = \int_{t_{0}}^{t} G_{i} (t, s) \sum_{j = 1}^{n} [σ_{i j} ((A_{j}^{- 1} y_{j}) (s)) - σ_{i j} ((A_{j}^{- 1} y_{j}^{*}) (s))] d ξ_{j} (s) .

Taking expectations for the above H_1i − H_3i, by Lemma 2.2 and (4.3), we have

E {|(z_{i} (t)|}^{2} \leq 3 E (| H_{1 i} |^{2} + | H_{2 i} |^{2} + | H_{3 i} |^{2}), i = 1,2, \dots, n . (4.4)

Evaluating the first term of the right-hand side of (4.4), by (3.2) we have

E | H_{1 i} |^{2} \leq e^{- 2 \underset{̲}{a_{i}} (t - t_{0})} E | z_{i} (t_{0}) |^{2} . (4.5)

Evaluating the second term of the right-hand side of (4.4), in view of Lemma 2.3, (3.2) and assumption (H₁), we have

\begin{aligned} E | H_{2 i} |^{2} & = E |\int_{t_{0}}^{t} G_{i} (t, s) [- a_{i} (s) c_{i} (s) [(A_{i}^{- 1} y_{i}) (s - γ) - (A_{i}^{- 1} y_{i}^{*}) (s - γ)] \\ + \sum_{j = 1}^{n} a_{i j} (s) [f_{j} ((A_{j}^{- 1} y_{j}) (s)) - f_{j} ((A_{j}^{- 1} y_{j}^{*}) (s))] \\ {+ \sum_{j = 1}^{n} d_{i j} (s) [g_{j} ((A_{j}^{- 1} y_{j}) (s - τ_{i j} (s))) - g_{j} ((A_{j}^{- 1} y_{j}^{*}) (s - τ_{i j} (s)))]] d s|}^{2} \\ \leq {[c_{i}^{*} {\bar{a}}_{i} {\bar{c}}_{i} + \sum_{j = 1}^{n} ({\bar{a}}_{i j} L_{j}^{f} c_{j}^{*} + {\bar{d}}_{i j} L_{j}^{g} c_{j}^{*})]}^{2} \int_{t_{0}}^{t} e^{- 2 \underset{̲}{a_{i}} (t - s)} E | z |_{1}^{2} d s . \end{aligned} (4.6)

As to the third term of the right-hand side of (4.4), in view of Lemma 2.1, Lemma 2.3, (3.2) and assumption (H₁), we also have

\begin{aligned} E | H_{3 i} |^{2} & = E {|\int_{t_{0}}^{t} G_{i} (t, s) \sum_{j = 1}^{n} [σ_{i j} ((A_{j}^{- 1} y_{j}) (s)) - σ_{i j} ((A_{j}^{- 1} y_{j}^{*}) (s))] d ξ_{j} (s)|}^{2} \\ = E |\int_{t_{0}}^{t} {|G_{i} (t, s) \sum_{j = 1}^{n} [σ_{i j} ((A_{j}^{- 1} y_{j}) (s)) - σ_{i j} ((A_{j}^{- 1} y_{j}^{*}) (s))]|}^{2} d s| \\ \leq {[\sum_{j = 1}^{n} l_{i j} c_{j}^{*}]}^{2} \int_{t_{0}}^{t} e^{- 2 \underset{̲}{a_{i}} (t - s)} E | z |_{1}^{2} d s . \end{aligned} (4.7)

From (4.4-4.7), we have

\begin{aligned} E {|(z_{i} (t)|}^{2} & \leq 3 e^{- 2 \underset{̲}{a_{i}} (t - t_{0})} E | z_{i} (t_{0}) |^{2} \\ + 3 [{(c_{i}^{*} {\bar{a}}_{i} {\bar{c}}_{i} + \sum_{j = 1}^{n} ({\bar{a}}_{i j} L_{j}^{f} c_{j}^{*} + {\bar{d}}_{i j} L_{j}^{g} c_{j}^{*}))}^{2} + {(\sum_{j = 1}^{n} l_{i j} c_{j}^{*})}^{2}]] \int_{t_{0}}^{t} e^{- 2 \underset{̲}{a_{i}} (t - s)} E | z |_{1}^{2} d s . \end{aligned} (4.8)

Using Gronwall-Bellman inequality and (4.8), we have

E {|z_{i} (t)|}^{2} \leq 3 E {|z_{i} (t_{0})|}^{2} e^{- λ (t - t_{0})}, (4.9)

where λ is defined by (4.1). Furthermore, form Lemma 2.3 and (4.9), we have

E {|x_{i} (t) - x_{i}^{*} (t)|}^{2} = E {|A_{i}^{- 1} z_{i} (t)|}^{2} \leq 3 {(c_{i}^{*})}^{2} E {|(z_{i} (t_{0})|}^{2} e^{- λ (t - t_{0})} .

Hence, the periodic solution of system (2.3) is globally exponentially stable, i.e., the periodic solution of system (2.1) is globally exponentially stable.

Corollary 4.1. Suppose that all conditions of Theorem 3.1 hold. Then, the periodic solution of system (2.1) is globally exponentially stable, provided that

\tilde{λ} = \min_{1 \leq i \leq n} \{2 \underset{̲}{a_{i}} - {\tilde{Λ}}_{i}\} > 0 a n d 3 {(c_{i}^{*})}^{2} > 1 i = 1,2, \dots, n,

where ${\tilde{Λ}}_{i}$ is defined by corollary 3.1.

Remark 4.1. From the above results, it is easy to see that the random terms have no effect on the periodicity of the considered system. That is, both stochastic neutral-type neural networks and its corresponding deterministic systems have the similar periodicity.

Remark 4.2. In recent years, fractional-order system have been extensively studied, see [45, 46] and related references. However, the periodic solution problems for fractional-order system or stochastic fractional-order system are rarely studied. In future research, we will focus on the aforementioned issues.

5 A numerical example

In this section, we present an example to illustrate the feasibility of our results obtained in previous sections. For i = 2, consider the following stochastic neutral-type neural networks:

\begin{aligned} d [x_{i} (t) - c_{i} (t) x_{i} (t - γ)] & = [- a_{i} (t) x_{i} (t) + \sum_{j = 1}^{n} a_{i j} (t) f_{j} (x_{j} (t)) + \sum_{j = 1}^{n} d_{i j} (t) g_{j} (x_{j} (t - τ_{i j} (t))) + I_{i} (t)] d t \\ + \sum_{j = 1}^{n} σ_{i j} (x_{j} (t)) d ξ_{j} (t), \end{aligned} (5.1)

where

c_{1} = c_{2} = 0.1, a_{1} (t) = 0.35 + 0.1 \sin t, a_{2} (t) = 0.4 + 0.1 \cos t, I_{1} (t) = I_{2} (t) = 0.2 \cos t,

{(a_{i j} (t))}_{2 \times 2} = (\begin{matrix} 0.2 + 0.1 \cos t & 0.1 + 0.25 \sin t \\ 0.3 + 0.25 \sin t & 0.2 + 0.05 \cos t \end{matrix}), {(d_{i j} (t))}_{2 \times 2} = (\begin{matrix} 0.25 + 0.1 \cos t & 0.15 + 0.25 \sin t \\ 0.25 + 0.2 \sin t & 0.3 + 0.15 \cos t \end{matrix}),

{(τ_{i j} (t))}_{2 \times 2} = (\begin{matrix} 0.5 + 0.2 \cos t & 0.3 + 0.15 \cos t \\ 0.3 + 0.1 \sin t & 0.4 + 0.2 \sin t \end{matrix}), {(σ_{i j} (x))}_{2 \times 2} = (\begin{matrix} 0.1 + 0.05 \cos x & 0.2 + 0.25 \sin x \\ 0.1 + 0.1 \sin x & 0.2 + 0.2 \cos x \end{matrix}),

f_{1} (x) = f_{2} (x) = 0.05 | x |, g_{1} (x) = g_{2} (x) = 0.01 | x | .

After a simple calculation, we have

\underset{̲}{a_{1}} = 0.25, \underset{̲}{a_{2}} = 0.3, {\bar{a}}_{1} = 0.45, {\bar{a}}_{2} = 0.5, {\bar{c}}_{1} = {\bar{c}}_{2} = 0.1, c_{1}^{*} = c_{2}^{*} = 1.1,

{\bar{a}}_{11} = 0.3, {\bar{a}}_{12} = 0.35, {\bar{a}}_{21} = 0.55, {\bar{a}}_{22} = 0.25, {\bar{d}}_{11} = 0.35, {\bar{d}}_{12} = 0.4, {\bar{d}}_{21} = 0.45, {\bar{d}}_{22} = 0.45,

L_{1}^{f} = L_{2}^{f} = 0.05, L_{1}^{g} = L_{2}^{g} = 0.01, l_{11} = 0.05, l_{12} = 0.25, l_{21} = 0.1, l_{22} = 0.2 .

Thus,

Λ_{1} = {(c_{1}^{*} {\bar{a}}_{1} {\bar{c}}_{1} + \sum_{j = 1}^{2} ({\bar{a}}_{1 j} L_{j}^{f} c_{j}^{*} + {\bar{d}}_{1 j} L_{j}^{g} c_{j}^{*}))}^{2} + {(\sum_{j = 1}^{2} l_{1 j} c_{j}^{*})}^{2} \approx 0.026,

Λ_{2} = {(c_{2}^{*} {\bar{a}}_{2} {\bar{c}}_{2} + \sum_{j = 1}^{2} ({\bar{a}}_{2 j} L_{j}^{f} c_{j}^{*} + {\bar{d}}_{2 j} L_{j}^{g} c_{j}^{*}))}^{2} + {(\sum_{j = 1}^{2} l_{2 j} c_{j}^{*})}^{2} \approx 0.023,

δ = \max_{1 \leq i \leq 2} \{\frac{2 Λ_{i}}{{\underset{̲}{a_{i}}}^{2}}\} \approx 0.9904 < 1,

λ = \min_{1 \leq i \leq 2} \{2 \underset{̲}{a_{i}} - Λ_{i}\} \approx 0.474 > 0, 3 {(c_{1}^{*})}^{2} = 3 {(c_{2}^{*})}^{2} = 3.63 > 1 .

It follows that all conditions of Theorem 4.1 hold. Hence, system (5.1) has a periodic solution, which is globally exponentially stable. The numerical solutions with different initial values are shown in Figure 1 and Figure 2.

Figure 1

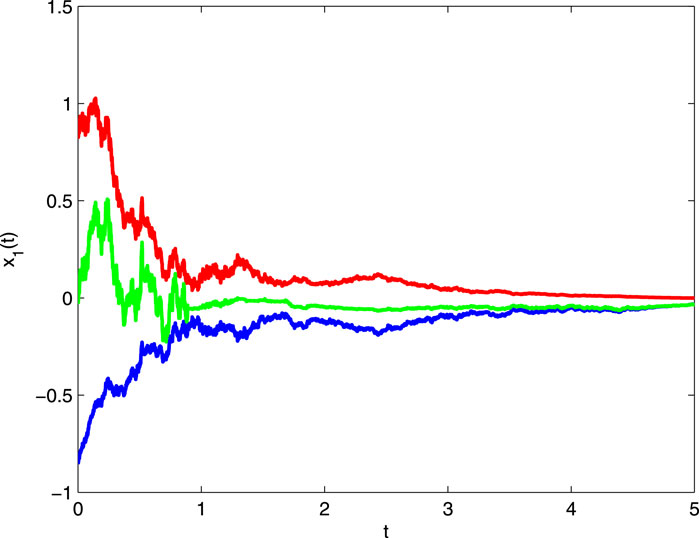
Figure 1. The states’ evolution of x₁(t) for Eq. 5.1 with different initial values.

Figure 2

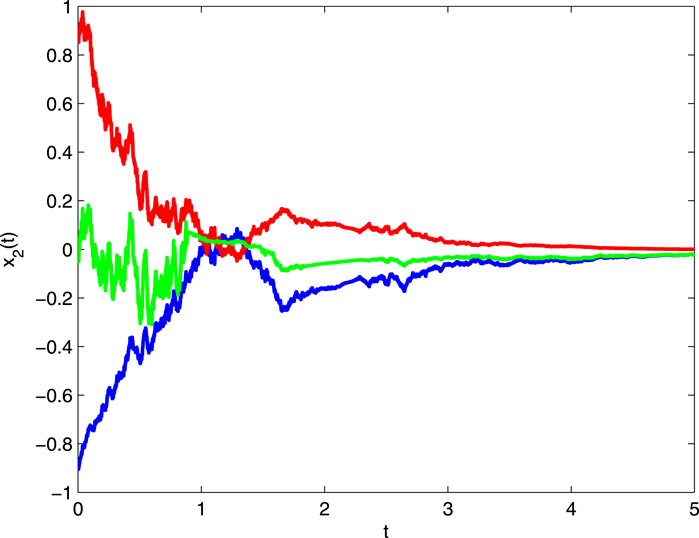
Figure 2. The states’ evolution of x₂(t) for Eq. 5.1 with different initial values.

6 Conclusion and discussions

In this paper, we have obtained some new sufficient conditions for the existence, uniqueness and exponential stability of periodic solution for a stochastic neutral-type neural networks with delays. The existence results have been obtained by the contraction mapping theorem which extend the previous corresponding results. The stability results have been obtained by stochastic analysis and Gronwall-Bellman inequality. It should be pointed out that the properties of neutral type operators have important applications in this study. We believe that the above properties can also be used to study other types of neutral-type neural networks.

In the future, we will explore existence and stability of periodic solution for neutral-type stochastic differential system with impulse, markov jumps, L $\overset{́}{e}$ vy jumps and so on. Also, we will study periodic solution problems for neutral-type stochastic differential system on time scales.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

FZ: Methodology, Funding acquisition, Writing–review and editing. XL: Methodology, Funding acquisition, Investigation, Writing–review and editing. BD: Writing–original draft, Methodology.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work is supported by the National Natural Science Foundation of China (No. 11971197) and Doctor Training Program of Jiyang College, Zhejiang Agriculture and Forestry University (RC2022D03).

Acknowledgments

The authors would like to thanks the editor and the referees for their valuable comments and suggestions, that improve the quality of our paper.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Has’minskii R. Stochastic stability of differential equations. Maryland: Sijthoff and Noordhoff (1980).

Google Scholar

2. It$\hat{o}$ K. On stochastic differential equations. Mem Amer Math Soc (1951)(4). doi:10.1090/memo/0004

CrossRef Full Text | Google Scholar

3. Lu KN, Schmalfuss B. Invariant manifolds for stochastic wave equations. J Differential Equation (2007) 236:460–92. doi:10.1016/j.jde.2006.09.024

CrossRef Full Text | Google Scholar

4. Mao XR. Exponential stabiity of stochastic differential equations. New York: Marcel Dekker, Inc (1994).

Google Scholar

5. ∅ksendal B. Stochastic differential equations: an introduction with applications. Berlin, Germany: Springer-Verlag (2003).

Google Scholar

6. Kolmanovskii VB, Myshkis A. Introduction to the theory and application of functional differential equations. London: Springer (1999).

Google Scholar

7. It\hat{o} K, Nisio M. On stationary solutions of a stochastic differential equation. J Math Kyoto Univ (1964) 4:1–75. doi:10.1215/kjm/1250524705

CrossRef Full Text | Google Scholar

8. Has’minskii RZ. On the dissipativity of random processes defined by differential equations. Probl Inf Transm (1965) 1:88–104.

Google Scholar

9. Xu D, Huang Y, Yang Z. Existence theorems for periodic Markov process and stochastic functional differential equations. Discrete Contin Dyn Syst (2009) 24:1005–23. doi:10.3934/dcds.2009.24.1005

CrossRef Full Text | Google Scholar

10. Li D, Xu D. Periodic solutions of stochastic delay differential equations and applications to Logistic equation and neural netwoks. J Korean Math Soc (2013) 50:1165–81. doi:10.4134/jkms.2013.50.6.1165

CrossRef Full Text | Google Scholar

11. Zhang B, Gopalsamy K. On the periodic solution of n-dimensional stochastic population models. Stochastic Anal Appl (2000) 18:323–31. doi:10.1080/07362990008809671

CrossRef Full Text | Google Scholar

12. Zhou H, Zhou Z, Qiao Z. Mean-square almost periodic solution for impulsive stochastic Nicholson’s blowflies model with delays. Appl Math Comput (2013) 219:5943–8. doi:10.1016/j.amc.2012.12.005

CrossRef Full Text | Google Scholar

13. Jiang D, Shi N. A note on nonautonomous logistic equation with random perturbation. J Math Anal Appl (2005) 303:164–72. doi:10.1016/j.jmaa.2004.08.027

CrossRef Full Text | Google Scholar

14. Jiang D, Shi N, Li X. Global stability and stochastic permanence of a non-autonomous logistic equation with random perturbation. J Math Anal Appl (2008) 340:588–97. doi:10.1016/j.jmaa.2007.08.014

CrossRef Full Text | Google Scholar

15. Liang J, Wang Z, Liu Y, Liu X. Robust synchronization of an array of coupled stochastic discrete-time delayed neural networks. IEEE Trans Neural Netw (2008) 19:1910–21. doi:10.1109/tnn.2008.2003250

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Tang Y, Wong WK. Distributed synchronization of coupled neural networks via randomly occurring control. IEEE Trans Neural Netw Learn Syst (2013) 24:435–47. doi:10.1109/tnnls.2012.2236355

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Zhu Q, Cao J. Exponential stability of stochastic neural networks with both Markovian jump parameters and mixed time delays. IEEE Trans Syst Man Cybern B, Cybern (2011) 41:341–53. doi:10.1109/TSMCB.2010.2053354

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Zhu Q, Cao J. Stability of Markovian jump neural networks with impulse control and time varying delays. Nonlinear Anal Real World Appl (2012) 13:2259–70. doi:10.1016/j.nonrwa.2012.01.021

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Wu X, Tang Y, Zhang W. Stability analysis of switched stochastic neural networks with time-varying delays. Neural Netw (2014) 52:39–49. doi:10.1016/j.neunet.2013.12.001

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Li C, Chen L, Aihara K. Impulsive control of stochastic systems with applications in chaos control, chaos synchronization, and neural networks. Chaos (2008) 18:023132. doi:10.1063/1.2939483

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Tojtovska B, Jankovi$\acute{c}$ S. On some stability problems of impulsive stochastic Cohen-Grossberg neural networks with mixed time delays. Appl Math Comput (2014) 239:211–26. doi:10.1016/j.amc.2014.04.038

CrossRef Full Text | Google Scholar

22. Zhang W, Tang Y, Wong W, Miao Q. Stochastic stability of delayed neural networks with Local impulsive effects. IEEE Trans Neural Netw Learn Syst (2015) 26:2336–45. doi:10.1109/tnnls.2014.2380451

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Zhang Z, Liu K. Existence and global exponential stability of a periodic solution to interval general bidirectional associative memory (BAM) neural networks with multiple delays on time scales. Neural Netw (2011) 24(5):427–39. doi:10.1016/j.neunet.2011.02.001

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Zhang Z, Cao J, Zhou D. Novel LMI-Based condition on global asymptotic stability for a class of Cohen-Grossberg BAM networks with extended activation functions. IEEE Transcation Neural Netw Learn Syst (2014) 25(6):1161–72. doi:10.1109/TNNLS.2013.2289855

CrossRef Full Text | Google Scholar

25. Wu W, Yang L, Ren Y. Periodic solutions for stochastic Cohen-Grossberg neural networks with time-varying delays. IJNSNS (2021) 22:13–21. doi:10.1515/ijnsns-2019-0142

CrossRef Full Text | Google Scholar

26. Yang L, Li Y. Existence and exponential stability of periodic solution for stochastic Hopfield neuralnet works on time scales. Neurocomputing (2015) 167:543–50. doi:10.1016/j.neucom.2015.04.038

CrossRef Full Text | Google Scholar

27. Wang F, Wu H. Mean square exponential stability and periodic solutions of stochastic interval neural networks with mixed time delays. Neurocomputing (2010) 73:3256–63. doi:10.1016/j.neucom.2010.04.020

CrossRef Full Text | Google Scholar

28. Zhao J, Shao Y. Stochastic periodic solution and permanence of a holling-leslie predator-prey system with impulsive effects. J Math (2021) 2021:1–19. doi:10.1155/2021/6694479

CrossRef Full Text | Google Scholar

29. Xiang J, Tan M. Dynamic behavior analysis of Stepanov-like almost periodic solution in distribution sense for stochastic neural network with delays. Neurocomputing (2022) 471:94–106. doi:10.1016/j.neucom.2021.10.108

CrossRef Full Text | Google Scholar

30. Mu X, Jiang D, Hayat T, Alsaedi A, Ahmad B. Stationary distribution and periodic solution of a stochastic Nicholson’s blowflies model with distributed delay. Math Methods Appl Sci (2021) 44:13756–73. doi:10.1002/mma.7656

CrossRef Full Text | Google Scholar

31. Arbi A, Tahri N. Stability analysis of inertial neural networks: a case of almost anti-periodic environment. Math Methods Appl Sci (2022) 45:10476–90. doi:10.1002/mma.8379

CrossRef Full Text | Google Scholar

32. Arbi A, Tahri N. Almost anti-periodic solution of inertial neural networks model on time scales. MATEC Web of Conferences (2022) 355:02006. doi:10.1051/matecconf/202235502006

CrossRef Full Text | Google Scholar

33. Arbi A, Cao J, Es-saiydy M, Zarhouni M, Zitane M. Dynamics of delayed cellular neural networks in the Stepanov pseudo almost automorphic space. Discrete and Continuous Dynamical Systems-S (2022) 15:3097–109. doi:10.3934/dcdss.2022136

CrossRef Full Text | Google Scholar

34. Arbi A, Tahri N. New results on time scales of pseudo Weyl almost periodic solution of delayed QVSICNNs. Comput Appl Math (2022) 41:293. doi:10.1007/s40314-022-02003-0

CrossRef Full Text | Google Scholar

35. Lakshmanan S, Balasubramaniam P. New results of robust stability analysis for neutral-type neural networks with time-varying delays and Markovian jumping parameters¹The work of authors was supported by Department of Science and Technology, New Delhi, India, under the sanctioned No. SR/S4/MS:485/07. Can J Phys (2011) 89:827–40. doi:10.1139/p11-059

CrossRef Full Text | Google Scholar

36. Lakshmanan S, Balasubramaniam P. Delay-interval-dependent robust-stability criteria for neutral stochastic neural networks with polytopic and linear fractional uncertainties. Int J Comp Math (2011) 88(88):2001–15. doi:10.1080/00207160.2010.537329

CrossRef Full Text | Google Scholar

37. Balasubramaniam P, Lakshmanan S, Rakkiyappan R. Delay-interval dependent robust stability criteria for stochastic neural networks with linear fractional uncertainties. Neurocomputing (2009) 72:3675–82. doi:10.1016/j.neucom.2009.06.006

CrossRef Full Text | Google Scholar

38. Wu F, Hu S, Liu Y. Positive solution and its asymptotic behaviour of stochastic functional Kolmogorov-type system. J Math Anal Appl (2010) 364:104–18. doi:10.1016/j.jmaa.2009.10.072

CrossRef Full Text | Google Scholar

39. Du B, Guo L, Ge W, Lu S. Periodic solutions for generalized Liénard neutral equation with variable parameter. Nonlinear Anal (2009) 70:2387–94. doi:10.1016/j.na.2008.03.021

CrossRef Full Text | Google Scholar

40. Hale J, Lunel S. An introduction to functional differential equations. Berlim, Germany: Springer-Verlag (1993).

Google Scholar

41. Li B, Cao Y, Li Y. Almost periodic oscillation in distribution for octonion-valued neutral-type stochastic recurrent neural networks with D operator. Nonlinear Dyn (2023) 111:11371–88. doi:10.1007/s11071-023-08411-z

CrossRef Full Text | Google Scholar

42. Li Z, Lam J, Fang R. Mean square stability of linear stochastic neutral-type time-delay systems with multiple delays. J Robust Nonlinear Control (2019) 29:451–72. doi:10.1002/rnc.4400

CrossRef Full Text | Google Scholar

43. Huang C, Yang H, Cao J. Weighted pseudo almost periodicity of multi-proportional delayed shunting inhibitory cellular neural networks with D operator. Dyn Syst Ser (2021) 14:1259–72. doi:10.3934/dcdss.2020372

CrossRef Full Text | Google Scholar

44. Du B, Wang H, Liu M, Cheng X. On the periodic solution of a class of stochastic nonlinear system with delays. J Nonlinear Sci Appl (2018) 11:263–73. doi:10.22436/jnsa.011.02.08

CrossRef Full Text | Google Scholar

45. Martinez-Fuentes O, Martinez-Guerra R. A high-gain observer with Mittag-Leffler rate of convergence for a class of nonlinear fractional-order systems. Commun nonlinear Sci Numer simulation (2019) 79:104909. doi:10.1016/j.cnsns.2019.104909

CrossRef Full Text | Google Scholar

46. Martinez-Fuentes O, Martinez-Guerra R. A novel Mittag-Leffler stable estimator for nonlinear fractional-order systems: a linear quadratic regulator approach. Nonlinear Dyn (2018) 94:1973–86. doi:10.1007/s11071-018-4469-6

CrossRef Full Text | Google Scholar

Keywords: periodic solution, stochastic, neutral-type neural networks, existence, exponential stability

Citation: Zheng F, Li X and Du B (2024) Periodic solution problems of neutral-type stochastic neural networks with time-varying delays. Front. Phys. 12:1338799. doi: 10.3389/fphy.2024.1338799

Received: 15 November 2023; Accepted: 20 March 2024;
Published: 05 April 2024.

Edited by:

Grienggrai Rajchakit, Maejo University, Thailand

Reviewed by:

Balasubramaniam. P, The Gandhigram Rural Institute, India
Peiluan Li, Henan University of Science and Technology, China

Copyright © 2024 Zheng, Li and Du. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Xiaoliang Li, lixiaoliang@zafu.edu.cn; Bo Du, dubo7307@163.com

ORIGINAL RESEARCH article

Periodic solution problems of neutral-type stochastic neural networks with time-varying delays

1 Introduction

2 Preliminaries

3 Existence of periodic solution

4 Globally exponential stability of periodic solution

5 A numerical example

6 Conclusion and discussions

Data availability statement

Author contributions

Funding

Acknowledgments

Conflict of interest

Publisher’s note

References

People also looked at