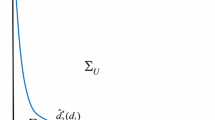Abstract
This paper is concerned with the global dynamics of a two-species Grindrod clustering model with Lotka–Volterra competition. The model takes the advective flux to depend directly upon local population densities without requiring intermediate signals like attractants or repellents to form the aggregation so as to increase the chances of survival of individuals like human populations forming small nucleated settlements. By imposing appropriate boundary conditions, we establish the global boundedness of solutions in two-dimensional bounded domains. Moreover, we prove the global stability of spatially homogeneous steady states under appropriate conditions on system parameters, and show that the rate of convergence to the coexistence steady state is exponential while the rate of convergence to the competitive exclusion steady state is algebraic.
Similar content being viewed by others
1 Introduction
The reaction-diffusion systems have been advocated to interpret numerous biological phenomena such as wave propagations [13, 41], pattern formation [16, 25], ecological invasions [11, 19], competition of species [18, 23], wound healing [39], and so on (cf. [5, 33]). However, in many biological processes involving directed motions, such as chemotaxis and predators seeking prey (prey-taxis), reaction-diffusion models may not be adequate to describe how organisms move and disperse. For instance, Rowell in [37] explains how models with random diffusion fail to explain certain ecological phenomena and do not accurately reflect the non-Brownian motion of individuals. The Lotka–Volterra type predator–prey system with random diffusion only is unable to produce spatial patterns (cf. [47]) to interpret the spatiotemporal heterogeneity observed in the field experiment [24, 45]. Rational movement along resource gradients has been thought to reduce the diffusive effect and result in clustering and formation of colonies to increase the chances of survival of individuals like human populations forming small nucleated settlements which grow as the population saturates locally. Incorporating both random and rational movements, Grindrod [15] proposed models of individual clustering in single-species and multi-species communities by taking the advective flux to depend directly upon local population densities without requiring intermediate signals like attractants or repellents.
Let us first briefly review the origin of Grindrod clustering models [15]. Classically, models for the spatial dispersion of biological populations have the form
where u(x, t) denotes the population density at location x and time t, and f(u, x, t) represents population kinetics due to the birth and death; \(\phi \) satisfies \(\phi (0)=0\) and \(\phi '(u)>0\) for \(u>0\). As highlighted in [15], the above model contains no aggregation mechanism such as swarming, herding, and clustering of individuals, which can serve as a balancing factor between death and birth rates and increase survival chances. To incorporate this phenomenon, a modified population balance equation reads
where \(\varvec{V}\) and E are the average velocity of individuals and the net rate of reproduction per individual, respectively. E typically has the form
Considering random diffusion with a probability \(\delta \in (0,1)\), and deterministic dispersion with the probability \(1-\delta \) in an average velocity \(\textbf{w}\) to increase the expected net rate of reproduction, \(\varvec{V}\) responding to u and E is given by \(\varvec{V}=-\delta \frac{\nabla u}{u}+(1-\delta )\textbf{w}\). The former obeys Fickian diffusion \(\frac{\nabla u}{u}\), while the latter is supposed to increase the net rate of reproduction per individual, such as \(\textbf{w}\approx \lambda \nabla E\) with \(\lambda >0\). This leads to the following model [15]
where \(\varepsilon >0\) is a small constant accounting for the small fluctuation to smooth out any sharp local variations in \(\nabla E\). After some rescalings, and assuming that the environment is homogeneous, the single-species model proposed in [15] reads
where \(\Omega \subset \mathbb {R}^{n}\) \((n \ge 2)\) is a bounded domain with a smooth boundary, Variables u(x, t) and E(u), and the parameter \(\varepsilon \) have the same meaning as above, \(\textbf{w}(x,t)\) denotes the average velocity increasing the expected rate of reproduction of individuals up to a rescaling. The parameters \(d, \chi , \gamma \) are all positive.
In the case of multi-species communities, the interspecific interactions (like competition or cooperation) between different species are indispensable. In particular the m-species Grindrod clustering model with competitive interactions reads as (cf. [15])
with
where all parameters \(d_{i}, \chi _{i}, \varepsilon _{i}, a_{i}, b_{i j}\) are positive. The original no-flux boundary condition (i.e. no individuals can cross the boundary) proposed in [15, formula (2.4)] for the two-species Grindrod clustering model (i.e., \(m=2\)) is
where \(\textbf{n}\) denotes the unit outer normal vector to the boundary \(\partial \Omega \). However, the above boundary condition \(\textbf{w}_i \cdot \textbf{n}\mid _{\partial \Omega }=0\) for \(\textbf{w}_i\) is inadequate to warrant the global well-posedness of the model (1.2) in multi-dimensions (\(n\ge 2\)). This limitation was identified by Nasreddine [34,35,36] for the single-species Grindroid clustering model, where the additional boundary condition \(\frac{\partial \textbf{w}}{\partial \textbf{n}} \times \textbf{n}\mid _{\partial \Omega }=0\) is suggested for the velocity \(\textbf{w}\). Such a kind of boundary condition is not peculiar, see e.g. [12, 38] for other models incorporating this kind of boundary condition. Accordingly, for the m-species Grindroid clustering model (1.2), we incorporate the boundary condition \(\frac{\partial \textbf{w}_i}{\partial \textbf{n}} \times \textbf{n}\mid _{\partial \Omega }=0\) for \(\textbf{w}_i\) (\(i=1,2,\cdots ,m\)). Therefore, the boundary conditions of (1.2) to be considered are
As usual, for vectors \(\textbf{a}=(a_1,a_2,\cdots ,a_n)\) and \(\textbf{b}=(b_1,b_2,\cdots ,b_n)\), the cross product \(\textbf{a}\times \textbf{b}\) is the number \(a_1b_2-a_2b_1\) if \(n=2\) and the vector \((a_{2} b_{3}-a_{3} b_{2},a_{1} b_{3}-a_{3} b_{1},a_{1} b_{2}-a_{2} b_{1})\) if \(n=3\). In one dimension (\(n=1\)), the condition \(\partial _{\textbf{n}}\textbf{w}_i\times \textbf{n}=\textbf{0}\) is not needed. The Dirchlet boundary condition \(\textbf{w}|_{\partial \Omega }=0\) satisfies the condition for \(\textbf{w}\) in (1.3). Though the Grindrod models were proposed three decades ago, there is no mathematical result available, except some preliminary results obtained for the single-species Grindrod model (1.1) with boundary conditions in (1.3). Nasreddine [34] proved the local-in-time existence of strong solutions of (1.1) with (1.3) in multi-dimensions for \((u, \textbf{w}) \in W^{1, p}(\Omega )\) with \(p>n\) and global existence of strong solutions to (1.1) in one dimension with (1.3) for both monostable and bistable functions E(u) as well as \(L^{2}\) convergence of solutions to constant steady states in the monostable case. The global existence of strong solutions of (1.1) with (1.3) in two dimensions was later established in [36], where the solution bound in \(W^{1, p}(\Omega )\) depends on time and the possibility of blow-up at infinite time was not precluded. The diffusion vanishing problem of (1.1) with (1.3) as \(\varepsilon \rightarrow 0\) in one dimension was investigated in [35], and the existence of traveling wave solutions of (1.1) in \(\mathbb {R}\) was established in [21] for \(E(u)=1-u\). The planar and radial traveling wave solutions of single-species and two-species Grindrod models with monostable function E(u) in \(\mathbb {R}^{n}\) was investigated in [26] alongside numerical simulations and found that directed motion can have substantial impacts not only on wave speed but also on the existence and structure of emergent patterns. The pattern formation of the two-species Grindrod model (i.e. (1.2) with \(m=2)\) with (1.3) in a two-dimensional convex domain was studied in [27], by assuming \(\textbf{w}_{i}=\nabla \phi _{i}\) for some potential functions \(\phi _{i}\) \((i=1,2)\), for three interspecific interactions: competition, generalist predator–prey and predator–prey. In particular, how the advective dispersal of species in heterogeneous resources and hazards leads to asymptotic steady states that retain spatial aggregation or clustering in regions of resource abundance and away from hazards was examined. By investigating pattern formation of the multi-species Grindrod model (1.2) approximated by a non-local cross-diffusion model, the authors of [40] proved that the Turing patterns, which were impossible for the two-species models, may arise for m-species Grindrod models with \(m \ge 3\).
From the above literature review, we see that the qualitative understanding of the Grindrod clustering models remains poorly understood, especially whether the solution blows up in infinite time in multi-dimensions is inconclusive and the large-time behavior of solutions is also unclear. This paper is devoted to exploring these basic questions. Without loss of generality, we consider the two-species Grindrod clustering model with competitions
with
where \(\Omega \subset \mathbb {R}^{2}\) is a bounded domain with a smooth boundary and \(\textbf{n}\) is the unit outward normal vector of \(\partial \Omega \), and all parameters \(d_{i}, \chi _{i}, \varepsilon _{i}, \gamma _{i}, b, c\), \(i\in \left\{ 1,2\right\} \), are positive. We underline that the boundary conditions in (1.4) (see also (1.3)) means that \(\partial _{\textbf{n}} \textbf{w}_i\) is parallel to \(\textbf{n}\) on \(\partial \Omega \), which along with the boundary condition \(\textbf{w}_{i} \cdot \textbf{n}\mid _{\partial \Omega }=0\) implies
We remark that without advection (i.e. \(\chi _1=\chi _2=0\)), the first two equations of (1.4)–(1.5) have no components \(\textbf{w}_{i} (i=1,2)\) and become the well-known competition-diffusion Lotka–Volterra model which has been well studied (cf. [4, 30]). The competition models with advection have also been widely studied in literatures (cf. [1, 2, 6,7,8,9, 14, 50]). All these works have assumed that the advection is biased to the concentration gradient of given resources. The competition dynamics in advective environments like the river or stream were also studied (cf. [29, 31]). We refer to [48, 49] for the study of global dynamics of diffusion-advection competition models with more general diffusive and/or advective coefficients. When the advection is modeled by the prey-taxis in a predator–prey system, the competition dynamics were investigated in [44]. Evidently, the advection considered in the Grindrod model (1.4)–(1.5) are different from those considered in the existing studies mentioned above.
In this paper, we shall establish the global boundedness and time-asymptotic dynamics of solutions to (1.4). Our first result concerning the global existence and boundedness of classical solutions is stated in the following theorem.
Theorem 1.1
Let \(\Omega \subset \mathbb {R}^{2}\) be a bounded domain with a smooth boundary. Assume \(u_{10}, u_{20} \in W^{1, p}(\Omega )\) with \(p>2\) and \(u_{10}, u_{20}\gvertneqq 0\). Then the system (1.4) admits a unique classical solution \((u_1, u_2, \textbf{w}_1, \textbf{w}_2)\) satisfying
and \(u_1,u_2>0\) in \({\Omega } \times (0, \infty )\). Moreover, there exists a positive constant C independent of t such that
Next, we explore asymptotic dynamics of (1.4). Except the extinction steady state \((0,0,\textbf{0},\textbf{0})\), the system (1.4) has three possible homogeneous steady states \(\left( u_{1s}, u_{2s},\textbf{0},\textbf{0}\right) \) depending on the value of parameters \(b,c,\gamma _1,\gamma _2\). They can be classified into the following three categories similar to the classical Lotka–Volterra competition system (cf. [30]):
-
Case 1. Weak competition: \(c<\frac{\gamma _1}{\gamma _2}<\frac{1}{b}\).
-
Case 2. Competitive exclusion: \(\frac{\gamma _1}{\gamma _2}<\min \{\frac{1}{b},c\}\) (resp. \(\frac{\gamma _1}{\gamma _2}>\max \{\frac{1}{b},c\}\)).
-
Case 3. Strong competition: \(\frac{1}{b}<\frac{\gamma _1}{\gamma _2}<c\).
Then the corresponding homogeneous steady state \(\left( u_{1\,s}, u_{2\,s},\textbf{0},\textbf{0}\right) \) can be solved as follows:
where
To state our main results on the large time behavior of solutions, we introduce some notations. Denote the function
and define two positive constants
Moreover, when \(c<\frac{\gamma _1}{\gamma _2}<\frac{1}{b}\) (weak competition), define two positive constants
and
Our second result is stated in the following.
Theorem 1.2
Suppose that the conditions in Theorem 1.1 hold. Then the solution \((u_1, u_2, \textbf{w}_1, \textbf{w}_2)\) of the system (1.4) obtained in Theorem 1.1 has the following convergence properties.
-
(i)
Assume \(c<\frac{\gamma _1}{\gamma _2}<\frac{1}{b}\) and \(({u_1^*},{u_2^*})\) is given by (1.8). If \((K_1,K_2)\) defined in (1.10) satisfies
$$\begin{aligned} K_1> f(b,c){u_1^*}\quad \text {and}\quad K_2>K_2^*, \end{aligned}$$(1.13)or
$$\begin{aligned} K_2> f(b,c){u_2^*}\quad \text {and}\quad K_1>K_1^*, \end{aligned}$$(1.14)then there exist positive constants C and \(\lambda \) independent of t such that
$$\begin{aligned} \sum _{i=1}^2\left( \left\| u_i(\cdot , t)-u_{i}^{*}\right\| _{{W^{1,\infty }(\Omega )}} +\left\| \textbf{w}_i\right\| _{{W^{1,\infty }(\Omega )}}\right) \le C e^{-\lambda t}\quad \text {as }t\rightarrow \infty . \end{aligned}$$ -
(ii)
Assume \(\frac{\gamma _1}{\gamma _2}<\min \{\frac{1}{b},c\}\). If
$$\begin{aligned} K_2> f\left( b,\frac{\gamma _1}{\gamma _2}\right) \gamma _2=\frac{\gamma _2^2+b^2\gamma _1^2}{\gamma _2-b\gamma _1}, \end{aligned}$$(1.15)then there exists a positive constant C independent of t such that
$$\begin{aligned}{} & {} \left\| u_1(\cdot , t)\right\| _{{W^{1,\infty }(\Omega )}}+\left\| u_2(\cdot , t)-\gamma _2\right\| _{{W^{1,\infty }(\Omega )}}\\{} & {} \qquad \quad +\sum _{i=1}^2\left\| \textbf{w}_i\right\| _{{W^{1,\infty }(\Omega )}}\le \frac{C}{1+t}\quad \text {as }t\rightarrow \infty . \end{aligned}$$ -
(iii)
Assume \(\frac{\gamma _1}{\gamma _2}>\max \{\frac{1}{b},c\}\). If
$$\begin{aligned} K_1> f\left( \frac{\gamma _2}{\gamma _1},c\right) \gamma _1=\frac{\gamma _1^2+c^2\gamma _2^2}{\gamma _1-c\gamma _2}, \end{aligned}$$then there exists a positive constant C independent of t such that
$$\begin{aligned}{} & {} \left\| u_1(\cdot , t)-\gamma _1\right\| _{{W^{1,\infty }(\Omega )}}+\left\| u_2(\cdot , t)\right\| _{{W^{1,\infty }(\Omega )}}\\{} & {} +\sum _{i=1}^2\left\| \textbf{w}_i\right\| _{{W^{1,\infty }(\Omega )}}\le \frac{C}{1+t}\quad \text {as }t\rightarrow \infty . \end{aligned}$$
Remark 1.1
It is unclear whether the parameter regime of \((K_1,K_2)\) satisfying (1.13) or (1.14) in Theorem 1.2(i) is admissible. Below we shall confirm this and further show what the admissible regime looks like. First, one can check that \((K_1^*,K_2^*)\) defined by (1.11) and (1.12) satisfies
Viewing \(K_1^*\) and \(K_2^*\) as functions of \(K_2\) and \(K_1\) according to (1.11) and (1.12), respectively, we get
where
due to \(f(b,c)>1\). Therefore, \(K_1^*\) (resp. \(K_2^*\)) decreases monotonically with respect to \(K_2\in (f(b,c){u_2^*},+\infty )\) (resp. \(K_1\in (f(b,c){u_1^*},+\infty )\)). Let
then the region of \(\Sigma \) is showed in Fig. 1.
Illustration of \(\Sigma \) defined by (1.16)
The rest of this paper is organized as follows. In Sect. 2, we shall address the local existence of solutions to (1.4), and then we will use an extension criterion to prove that the local solution is actually uniformly bounded and exists globally in time in Sect. 3. In Sect. 4, we shall prove the global stabilities stated in Theorem 1.2 by constructing Lyapunov functionals along with compactness arguments.
2 Preliminaries: local existence and some inequalities
Before proceeding, we introduce some notations used throughout the paper.
Notations:
-
For brevity, we abbreviate \(\int _{0}^{t} \int _{\Omega } f(\cdot , s) d x d s\) and \(\int _{\Omega } f(\cdot , t) d x\) as \(\int _{0}^{t} \int _{\Omega } f\) and \(\int _{\Omega } f\), respectively. In addition, C and \(C_{i}\) \((i=1,2,3, \cdots )\) stand for generic positive constants which may vary from line to line.
-
\(W^{k,p}(\Omega )=\{u\in L^p(\Omega ): D^\alpha u\in L^p(\Omega ) \ \text {for}\ 0\le |\alpha |\le k\} \) denotes the usual Sobolev space, where \(D^\alpha u\) is the weak partial derivative. If \(p=2\), we write \(H^k(\Omega )=W^{k,2}(\Omega )\).
In this section, we establish the local existence of solutions to the system (1.4) under appropriate initial conditions. Moreover, we shall collect and prove some useful inequalities which will be used in the subsequent sections. To begin with, we consider the regularity of the solution \(\textbf{w}\) to the following system:
where \(\mu \in \left\{ 0,1\right\} \) and \(\textbf{f} \in \left( L^{p}(\Omega )\right) ^{n}\) for some \(1<p<+\infty \). The system (2.1) has the following properties.
Lemma 2.1
(cf. [38, Theorem 3, Theorem 4, Remark 5]) Let \(\mu =0\) and \(\Omega \subset \mathbb {R}^{n}\), \(n\in \left\{ 2,3\right\} \), be a bounded domain with a smooth boundary.
-
(i)
If \(\textbf{f} \in \left( L^{p}(\Omega )\right) ^{n}\) with some \(1<p<+\infty \), then the system (2.1) has a unique solution \(\textbf{w}\in (W^{2, p}(\Omega ))^n\) satisfying
$$\begin{aligned} \Vert \textbf{w}\Vert _{W^{2, p}(\Omega )} \le C(p,n, \Omega )\Vert \textbf{f}\Vert _{{L^{p}(\Omega )}}, \end{aligned}$$(2.2)where \(C(p, n,\Omega )\) is a positive constant depending only on p, n and \(\Omega \).
-
(ii)
If \(\textbf{f} \in (C^{k,\alpha }(\bar{\Omega }))^n\) with some \(\alpha \in (0,1)\) and \(k\in \mathbb N\), then the system (2.1) has a unique solution \(\textbf{w}\in C^{k+2,\beta }(\bar{\Omega })\) for some \(\beta \in (0,1)\) and
$$\begin{aligned} \Vert \textbf{w}\Vert _{C^{k+2,\beta }(\bar{\Omega })} \le C(k,\alpha ,\beta ,n, \Omega )\Vert \textbf{f}\Vert _{C^{k,\alpha }(\bar{\Omega })}. \end{aligned}$$(2.3)where \(C(k,\alpha ,\beta ,n, \Omega )\) is a positive constant depending only on k, \(\alpha \), \(\beta \), n and \(\Omega \).
Now we prove the following results for the case \(\mu =1\).
Lemma 2.2
Let \(\mu =1\) and \(\Omega \subset \mathbb {R}^{n}\), \(n\in \left\{ 2,3\right\} \), be a bounded domain with a smooth boundary.
-
(i)
If \(\textbf{f} \in \left( H^{k}(\Omega )\right) ^{n}\) with \(k\in \left\{ 0,1,2\right\} \), then the system (2.1) has a unique solution \(\textbf{w}\in H^{k+2}(\Omega )\) satisfying
$$\begin{aligned} \Vert \textbf{w}\Vert _{H^{k+2}(\Omega )} \le C(k,n, \Omega )\Vert \textbf{f}\Vert _{H^{k}(\Omega )}, \end{aligned}$$(2.4)where \(C(k, n,\Omega )\) is a positive constant depending only on k, n and \(\Omega \).
-
(ii)
If \(\textbf{f} \in \left( L^{p}(\Omega )\right) ^{n}\) with some \(1<p<+\infty \), then the system (2.1) has a unique solution \(\textbf{w}\in (W^{2, p}(\Omega ))^n\) satisfying
$$\begin{aligned} \Vert \textbf{w}\Vert _{W^{2, p}(\Omega )} \le C(p,n, \Omega )\Vert \textbf{f}\Vert _{{L^{p}(\Omega )}}, \end{aligned}$$(2.5)where \(C(p, n,\Omega )\) is a positive constant depending only on p, n and \(\Omega \).
-
(iii)
If \(\textbf{f} \in (C^{k,\alpha }(\bar{\Omega }))^n\) with some \(\alpha \in (0,1)\) and \(k\in \left\{ 0,1,2\right\} \), then the system (2.1) has a unique solution \(\textbf{w}\in C^{k+2,\beta }(\bar{\Omega })\) for some \(\beta \in (0,1)\) and
$$\begin{aligned} \Vert \textbf{w}\Vert _{C^{k+2,\beta }(\bar{\Omega })} \le C(k,\alpha ,\beta ,n, \Omega )\Vert \textbf{f}\Vert _{C^{k,\alpha }(\bar{\Omega })}. \end{aligned}$$(2.6)where \(C(k,\alpha ,\beta ,n, \Omega )\) is a positive constant depending only on k, \(\alpha \), \(\beta \), n and \(\Omega \).
Proof
The existence and uniqueness of the solution to (2.1) for \(\mu =1\) can be established by similar arguments for (2.1) in the case of \(\mu =0\) (cf. [38]). Below we only prove the regularity properties given in (2.4)–(2.6).
(i) Since the proof of (2.4) involves tedious calculations, we place it in Appendix A (see Lemma A1 and Lemma A2 in Appendix A).
(ii) Next we prove (2.5). The first equation of (2.1) can be rewritten as
Therefore, in view of (2.2) and (2.7), it is sufficient to prove that for \(p\in (1,\infty )\), there exists a positive constant \(C(p,n,\Omega )\) such that
We consider three cases: \(p\ge 2\), \(\frac{6}{5}\le p<2\) and \(1<p<\frac{6}{5}\). First, if \(p\ge 2\), it follows from \(\textbf{f}\in ({L^{p}(\Omega )})^n\hookrightarrow ({L^{2}(\Omega )})^n \) for \(p\ge 2\) and (2.4) that \(\textbf{w}\in (H^{2}(\Omega ))^n\) with \(\left\| \textbf{w}\right\| _{H^2(\Omega )}\le C(p,n,\Omega )\Vert \textbf{f}\Vert _{L^{p}(\Omega )}\), which alongside the Sobolev embedding \((H^{2}(\Omega ))^n\hookrightarrow ({L^{p}(\Omega )})^n\) yields
and hence (2.8) holds for \(p\ge 2\). Secondly, if \(\frac{6}{5}\le p<2\), we claim that
To this end, we define the real Hilbert space (cf. [10])
Since \(H^1(\Omega )\hookrightarrow {L^{6}(\Omega )}\hookrightarrow {L^{p^*}(\Omega )}=({L^{p}(\Omega )})^*\) with \(p^*:=\frac{p}{p-1}\), we have \(\textbf{f}\in ({L^{p}(\Omega )})^n\hookrightarrow (H^{1}(\Omega ))^*\). Define the bilinear form \(B[\cdot ,\cdot ]\) on X by
Then we have
where we have used the fact that the X norm is equivalent to the usual \(H^1(\Omega )\) norm (cf. [12]). Moreover,
Therefore, by the Lax–Milgram theorem, we obtain that for each \(\textbf{f}\in ({L^{p}(\Omega )})^n\) with \(\frac{6}{5}\le p<2\), there exists a unique \(\textbf{u} _f\in X\) such that
Therefore, by (2.10), Hölder’s inequality, the Sobolev embedding \(H^1(\Omega )\hookrightarrow {L^{p^*}(\Omega )}\) and the equivalence of X norm and \(H^1(\Omega )\) norm, we have
for all \(\textbf{u} \in X\), that is
Therefore, the claim (2.9) is proved since the solution \(\textbf{w}\) to (2.1) satisfies \(\textbf{w}\in X\), and hence (2.8) holds for \(\frac{6}{5}\le p<2\) due to the Sobolev embedding \(H^1(\Omega )\hookrightarrow {L^{p}(\Omega )}\). It remains to consider the case \(1<p<\frac{6}{5}\). We let \(\alpha :=\frac{p}{3-2p}\in (1,2)\) which satisfies
Then \(|\textbf{w}|^\alpha =\left( \sum \limits _{i=1}^n w_i^2\right) ^\frac{\alpha }{2}\) satisfies
where we have used \(\textbf{w}\cdot \partial _{\textbf{n}}\textbf{w}=0\) on \(\partial \Omega \) due to the boundary conditions of \(\textbf{w}\) in (2.1). Integrating the first equation of (2.12) on \(\Omega \) by parts with \(\partial _{\textbf{n}}|\textbf{w}|^\alpha =0\) on \(\partial \Omega \) and using \(-\Delta \textbf{w}=\textbf{f}-\textbf{w}\) in \(\Omega \), one has
which together with \(\alpha -2<0\) and \(\int _\Omega |\textbf{w}|^{\alpha -4}|\textbf{w}\cdot \nabla \textbf{w}|^2\le \int _\Omega |\textbf{w}|^{\alpha -2}|\nabla \textbf{w}|^2\) implies
With (2.11) and (2.13), we are in a position to use the same arguments as in [38, pp. 133–134] to show that
By \(3\alpha >3\) and Hölder’s inequality: \({L^{3\alpha }(\Omega )}\hookrightarrow {L^{p}(\Omega )}\) for \(1<p<\frac{6}{5}\), we know that (2.8) holds for \(1<p<\frac{6}{5}\). Therefore, we have proved that (2.8) holds for \(p\in (1,\infty )\) as desired.
(iii) If \(\textbf{f} \in (C^{k,\alpha }(\bar{\Omega }))^n\) with some \(\alpha \in (0,1)\) and \(k\in \left\{ 0,1,2\right\} \), then (2.4) implies
which together with the Sobolev embedding \(H^{k+2}(\Omega )\hookrightarrow C^{k,\theta }(\bar{\Omega })\) for any \(\theta \in \left( 0,2-\frac{n}{2}\right) \) shows that
for any \(\alpha '\in (0,\min \left\{ \alpha ,\frac{1}{2}\right\} )\). In view of (2.3), (2.7) and (2.14), (2.6) is proved.
\(\square \)
We are now in a position to show the local existence of the unique classical solution to (1.4).
Lemma 2.3
Let \(\Omega \subset \mathbb {R}^2\) be a bounded domain with a smooth boundary. Assume \(u_{10}, u_{20} \in W^{1, p}(\Omega )\) with \(p>2\) and \(u_{10}, u_{20}\gvertneqq 0\). Then there exists \(T_{max} \in (0, \infty ]\) such that the system (1.4) has a unique classical solution \((u_1,u_2,\textbf{w}_1,\textbf{w}_2)\) satisfying
and \(u_1,u_2>0\) in \(\Omega \times (0, T_{max})\). Moreover,
Proof
Fix \(R>0\), and define for \(T \in (0,1)\)
which is a complete metric space with the metric
for \(\textbf{u}=(u_1(t),u_2(t))\in X_{R}(T)\) and \(\textbf{v} =(v_1(t),v_2(t))\in X_{R}(T) \). For any \(\textbf{u}=(u_1,u_2) \in X_{R}(T)\) and \(t \in [0, T]\), by \(p>2\) and Lemma 2.2 we know that there exists a unique solution \((\textbf{w}_1,\textbf{w}_2)\in \left( H^{2}(\Omega )\right) ^{2}\times \left( H^{2}(\Omega )\right) ^{2}\) to the following system
Letting \(\left( e^{t \Delta }\right) _{t \ge 0}\) denote the Neumann heat semigroup on \(\Omega \), we introduce a mapping \(\varvec{\Phi }=\left( \Phi _{1}, \Phi _{2}\right) \) on \(X_R(T)\) by defining
for \(i=1,2\), where \((\textbf{w}_1,\textbf{w}_2)\in \left( H^{2}(\Omega )\right) ^{2}\times \left( H^{2}(\Omega )\right) ^{2}\) is the solution of (2.16) uniquely determined by the given \(\textbf{u}=(u_1,u_2)\in X_{R}(T)\) according to Lemma 2.2. Then one can show that \(\varvec{\Phi }\) is a contraction map from \(X_{R}(T)\) into itself if T is sufficiently small by a standard argument (see e.g. [34, Theorem 2.2]). Therefore, for sufficiently small T, by the Banach fixed point theorem, there is a unique \((u_1,u_2) \in X_{R}(T)\) such that
and \((u_1,u_2,\textbf{w}_1,\textbf{w}_2)\) is a unique strong solution of the system (1.4) satisfying
Based on a bootstrap argument, we can use Lemma 2.2, the \(L^{p}\)-estimate and the Schauder estimate (cf. [28]) to show that the unique strong solution \((u_1,u_2,\textbf{w}_1,\textbf{w}_2)\) of the system (1.4) satisfying (2.17) is actually a classical solution. Finally, \(u_1\), \(u_2\ge 0\) follows from the maximum principle. To be precise, we rewrite the first equation of system (1.4) as
where \(Q_1(x,t):=\chi _1\nabla \cdot \textbf{w}_1-E_1(u_1,u_2)\) for \((x,t)\in \Omega \times (0,T)\). Then one can apply the strong maximum principle to system (2.18) and gets that \(u_1(x,t)>0\) for \((x,t)\in \Omega \times (0,T)\). Similarly, it holds that \(u_2(x,t)>0\) for \((x,t)\in \Omega \times (0,T)\). The proof is completed. \(\square \)
Next we prove a useful Lemma.
Lemma 2.4
Let \(\Omega \subset \mathbb {R}^n\), \(n\ge 1\), be a bounded domain with a smooth boundary, and let \(r,q\ge 1\) be two constants satisfying
Then for any \(\varphi \in H^{2}(\Omega )\) satisfying \(\left. \frac{\partial \varphi }{\partial \textbf{n}}\right| _{\partial \Omega }=0\), there exists a positive constant C depending only on \(\Omega \), n, q and r such that
where
Proof
First, one can use (2.19) to check that \(\theta \) defined by (2.20) satisfies \(\theta \in (0,1)\). Using the Gagliardo–Nirenberg inequality, we have
Under the homogeneous Neumann boundary condition \(\left. \frac{\partial \varphi }{\partial \textbf{n}}\right| _{\partial \Omega }=0\), it follows from [3, Lemma 1] that \(\Vert \nabla \varphi \Vert _{H^1(\Omega )} \le C\Vert \Delta \varphi \Vert _{{L^{2}(\Omega )}}\), which implies
The proof is completed by substituting (2.22) into (2.21). \(\square \)
We recall the following basic result which will be used to investigate the global stability of solutions.
Lemma 2.5
([43, Lemma 1.1]) Let \(\tau \ge 0\) and \(c>0\) be two constants, \(F(t) \ge 0, \int _{\tau }^{\infty } H(t) \textrm{d} t<\infty \). Assume that \(E \in C^{1}([\tau , \infty )), E\) is bounded from below and satisfies
If either \(F \in C^{1}([\tau , \infty ))\) and \(F^{\prime }(t) \le k\) in \([\tau , \infty )\) for some \(k>0,\) or \(F \in C^{\alpha }([\tau , \infty ))\) and \(\Vert F\Vert _{C^{\alpha }([\tau , \infty ))} \le k\) for constants \(0<\alpha <1\) and \(k>0\), then \(\lim _{t \rightarrow \infty } F(t)=0.\)
3 Boundedness of solutions
In this section, we focus on the global boundedness of solutions of the system (1.4). Throughout this section, we assume that the conditions in Theorem 1.1 hold and \((u_1, u_2,\textbf{w}_1,\textbf{w}_2)\) be a local-in-time classical solution of the system (1.4) obtained in Lemma 2.3 with a maximal time \(T_{max}\). First of all, we give the following basic property for the solution components \(\textbf{w}_1\) and \(\textbf{w}_2\).
Lemma 3.1
For \(i,j\in \left\{ 1,2\right\} \), the solution of (1.4) satisfies
Proof
Denote \(\textbf{w}_i=({w}_1^{(i)},{w}_2^{(i)})\), \(i=1,2\). Using integration by parts we get
By (1.6) we have
This together with (3.1) completes the proof. \(\square \)
The following result is a basic property about the uniform-in-time boundedness of \(u_1\) and \(u_2\) in \({L^{1}(\Omega )}\).
Lemma 3.2
Suppose that the conditions in Theorem 1.1 hold. Then for \(i=1,2\), it holds that
Proof
Integrating the first equation of (1.4) with respect to \(x\in \Omega \), and using \(\nabla u_{1} \cdot \textbf{n} \mid _{\partial \Omega }=\textbf{w}_1 \cdot \textbf{n} \mid _{\partial \Omega }=0\), \(u_1\), \(u_2>0\) and the Young’s inequality \(s\le \frac{1}{1+\gamma _1}s^2+\frac{1+\gamma _1}{4}\) for \(s\ge 0\), we have
An application of Grönwall’s inequality to (3.3) yields (3.2) for \(i=1\). Similarly, (3.2) holds for \(i=2\). This completes the proof. \(\square \)
Now we are in a position to derive the following estimates.
Lemma 3.3
Suppose that the conditions in Theorem 1.1 hold. Then there exist two constants \(k>0\) and \(C>0\) independent of t such that for all \(\tau \in [0,T_{max})\) and \(t\in (0,T_{max}-\tau )\), it hold that
and
Proof
Multiplying the first equation in (1.4) by \((\log u_1+1)\) and integrating the resulting equation by parts along with the boundary conditions in (1.4), we have
for all \(t\in (0,T_{max})\). For the first term on the right hand side of (3.6), using integration by parts subject to the boundary conditions \(\textbf{w}_1 \cdot \textbf{n} \mid _{\partial \Omega }=0\), one has
Multiplying the third equation of (1.4) by \(\textbf{w}_1\), integrating the resulting equation by parts along with the boundary conditions in (1.4), and using Lemma 3.1 and Young’s inequality, for all \(t\in (0,T_{max})\) one has
The combination of (3.6)–(3.7) shows that
for all \(t\in (0,T_{max})\). Similarly, for \(u_2\), it holds that
for all \(t\in (0,T_{max})\). Using (3.8) and (3.9), for all \(t\in (0,T_{max})\) one has
where \(q_1:=\frac{(2+\chi _1^2)}{\varepsilon _1}+\frac{2b^2}{\varepsilon _2}+1\) and \(q_2:=\frac{(2+\chi _2^2)}{\varepsilon _2}+\frac{2c^2}{\varepsilon _1}+1\). Clearly, the following results hold:
Making use of (1.5), (3.2) and (3.11), we obtain
The continuous function \(\phi (s):=s^2\left[ \log s-2(\gamma _1+q_1)\right] \) for \(s>0\) is bounded from below. In fact, \(\phi (s)>0\) for \(s\in (s_*,\infty )\) with \(s_*:=e^{2(\gamma _1+q_1)}>0\) and
where we have used the fact that \(s^2\log s\ge -\frac{1}{2e}\) for \(s\in (0,\infty )\). This along with (3.12) shows that
Similarly, one can deduce that
Substituting (3.13) and (3.14) into (3.10), one has
Finally, (3.4) is achieved by applying Grönwall’s inequality to (3.15), and (3.5) is obtained by (3.4) and an integration of (3.15) with respect to t. \(\square \)
With (3.5), we can obtain the following uniform-in-time estimates of \(\Vert u_1\Vert _{L^{q}(\Omega )}\) and \(\Vert u_2\Vert _{L^{q}(\Omega )}\) for \(q\in (1,\infty )\).
Lemma 3.4
Suppose that the conditions in Theorem 1.1 hold. For any \(1<q<\infty \), there exists a positive constant C(q) independent of t such that
Proof
Multiplying the first equation of (1.4) by \(q u_1^{q-1}\) for \(q>1\) and integrating the resulting equation by parts subject to the boundary condition \(\nabla u_{1} \cdot \textbf{n}\mid _{\partial \Omega }=\textbf{w}_1\cdot \textbf{n}\mid _{\partial \Omega }=0\), we have
By Hölder’s inequality we have
where it follows from the Gagliardo–Nirenberg inequality that
Substituting (3.19) into (3.18), and using Young’s inequality and Hölder’s inequality, for all \(t\in (0,T_{max})\), one has
Using Hölder’s inequality: \(\Vert u_1\Vert _{L^{q}(\Omega )}\le |\Omega |^{\frac{1}{q(q+1)}}\Vert u_1\Vert _{L^{q+1}(\Omega )}\) and Young’s inequality: \(q\gamma _1 u_1^q\le (q-1)u_1^{q+1}+\gamma _1^{q+1}C(q)\), we have
Then the combination of (3.17), (3.20) and (3.21) shows that
for all \(t\in (0,T_{max})\). Using (3.5), for all \(\tau \in (0,T_{max})\) and \(t\in (0,T_{max}-\tau )\), we have
With (3.23), one can apply a nonlinear Gronwall’s inequality shown in [22, Lemma 2.3] to (3.22) to obtain
Performing the same procedures as \(u_1\), one can deduce the following estimate for \(u_2\) as
which along with (3.24) completes the proof. \(\square \)
The following uniform-in-time estimates of \(\textbf{w}_1\) and \(\textbf{w}_2\) in \({W^{1,2}(\Omega )}\) can be easily obtained.
Lemma 3.5
Suppose that the conditions in Theorem 1.1 hold. Then there exists a positive constant C independent of t such that
Proof
In view of (3.7) and (3.16), we get \(\Vert \textbf{w}_1\Vert _{{W^{1,2}(\Omega )}}\le C\) for all \(t\in (0,T_{max})\). The estimate for \(\textbf{w}_2\) follows similarly. \(\square \)
Now we are in a position to derive the \(L^\infty \)-boundedness of \(u_1\) and \(u_2\) by the \(L^p\)-\(L^q\) estimates of the Neumann heat semigroup.
Lemma 3.6
Suppose that the conditions in Theorem 1.1 hold. Then there exists a positive constant C independent of t such that
Proof
It follows from (3.16), (3.25) and the Sobolev embedding \(W^{1,2}(\Omega )\hookrightarrow {L^{6}(\Omega )}\) that
where Hölder’s inequality was used. Now given \(t\in (0,T_{max})\), we let \(t_0:=(t-1)_+\). Applying the variation-of-constants formula, using \(u_1\), \(u_2\ge 0\) and the comparison principle, for all \(t\in (0,T_{max})\), one has
which implies
It follows from the well-known Neumann heat semigroup (cf. [32, Lemma 2.2], see also [46, formula (1.8)]) that
For \(t\ge 1\), \(t_0=t-1\) and hence we have along with (3.2)
Since \(u_{10}\in W^{1, p}(\Omega )\hookrightarrow {L^{\infty }(\Omega )}\) due to \(p>2\), it follows from the parabolic maximum principle that
For \(I_6\), using (3.27) and the smoothing property of the Neumann heat semigroup [46, Lemma 1.3 (ii)], we get
where \(\lambda _1\) denotes the smallest positive eigenvalue of \(-\Delta \) in \(\Omega \). Now it remains to estimate the term \(I_7\). Let \(\overline{u}_1(s):=\frac{1}{|\Omega |}\int _\Omega u_1(x,t)\). Then using \(t-t_0\le 1\), the smoothing property of the Neumann heat semigroup [46, Lemma 1.3 (i)], (3.2) and Lemma 3.4 with \(q=2\), we obtain
Now the combination of (3.28)–(3.32) yields
Similar arguments applied to \(u_2\) give
The proof is completed. \(\square \)
We next deduce the uniform-in-time estimates for \(\nabla u_1\) and \(\nabla u_2\) in \({L^{2}(\Omega )}\).
Lemma 3.7
Suppose that the conditions in Theorem 1.1 hold. Then there exists a positive constant C independent of t such that
Proof
Multiplying the first equation of (1.4) by \(-\Delta u_1\) and integrating the resulting equation by parts along with the boundary conditions in (1.4), one has
for all \(t\in (0,T_{max})\). With the boundary condition \(\nabla u_{1} \cdot \textbf{n}\mid _{\partial \Omega }=0\) and (3.26), we further have
Clearly, for all \(t\in (0,T_{max})\), it holds that
Making use of (3.25) and (3.26), for all \(t\in (0,T_{max})\), we obtain
Noticing that \(\nabla |\nabla z|^{2}=2 D^{2} z \cdot \nabla z\) for \(z \in C^{2}(\bar{\Omega })\) with \(D^2z=\nabla (\nabla z)\), we arrive at
where Hölder’s inequality and Lemma 3.5 have been used. Applying Lemma 2.4 (with \(q=4\), \(r=n=2\) and \(\theta =\frac{3}{4}\)) to \(\Vert \nabla u_1\Vert _{L^{4}(\Omega )}\) and using (3.26), (3.38) and Young’s inequality, for all \(t\in (0,T_{max})\), we have
The substitution of (3.37) and (3.39) into (3.36) yields
Using (3.26), (3.34), (3.35) and (3.40), for all \(t\in (0,T_{max})\), one can see that
Similar procedures applied to \(u_2\) yield that
for all \(t\in (0,T_{max})\). This along with (3.41) shows that
Applying Lemma 2.4 (with \(q=r=n=2\) and \(\theta =\frac{1}{2}\)) to \(\Vert \nabla u_i\Vert _{{L^{2}(\Omega )}}\) for \(i=1,2\) and using (3.26) and Young’s inequality, for all \(t\in (0,T_{max})\), we obtain
This together with (3.42) shows that
Applying Grönwall’s inequality to (3.43) leads to
which proves (3.33). \(\square \)
With (3.33), we can use Lemma 2.2 to derive the uniform-in-time estimates of \(\textbf{w}_1\) and \(\textbf{w}_2\) in \(H^2(\Omega )\) (Lemma 3.8), which along with the \(L^p\)-\(L^q\)-estimates of the Neumann heat semigroup enables us to further obtain the boundedness of \(\nabla u_1\) and \(\nabla u_2\) as stated in Lemma 3.9.
Lemma 3.8
Suppose that the conditions in Theorem 1.1 hold. Then there exists a positive constant C independent of t such that
Proof
From Lemma 2.2 and (3.33), (3.44) follows immediately. \(\square \)
Lemma 3.9
Suppose that the conditions in Theorem 1.1 hold. Then there exists a positive constant C independent of t such that
Proof
Applying the variation-of-constants formula, one has
where
It follows from (3.26), (3.33), (3.44) and the Sobolev embedding \(H^{2}(\Omega )\hookrightarrow {L^{\infty }(\Omega )}\) that
which along with (3.26) shows that
Now using the smoothing property of the Neumann heat semigroup [46, Lemma 1.3 (ii)] again, we obtain
In a similar manner, we have
which along with (3.26) and (3.46) completes the proof. \(\square \)
Proof of Theorem 1.1
\(T_{max}=\infty \) is a direct consequence (2.15) and (3.45). By (3.45) and Lemma 2.2, one can obtain (1.7) directly. \(\square \)
4 Global Stability
In this section, we shall investigate the asymptotic behavior of solutions to the system (1.4) and prove Theorem 1.2 by the Lyapunov functional method alongside compactness arguments. To begin with, we derive the following higher-order estimates of solutions when time t is away from 0.
Lemma 4.1
Suppose that the conditions in Theorem 1.1 hold. Then for any \(\theta \in (0,1)\), there exists a positive constant \(C(\theta )\) such that
Proof
It follows from (1.7) that
Taking \(t_0=\frac{1}{8}\) as the initial time, then \(u_1(\cdot ,t_0),u_2(\cdot ,t_0)\in {W^{1,p}(\Omega )}\). Using a similar argument as in the proof of Lemma 3.9, for any \(q\in (1,\infty )\), one can find a positive constant C(q) such that
Then using Lemma 2.2 and (4.2) one has
For any \(\theta \in (0,1)\), using (4.3) and the Sobolev embedding \(W^{2,r}(\Omega )\hookrightarrow C^{1,1-\frac{2}{r}}(\bar{\Omega })\hookrightarrow C^{1,\theta }(\bar{\Omega })\) for \(r>\frac{2}{1-\theta }\), we can find some \(r_0>\frac{2}{1-\theta }\) and \(C(\theta )>0\) such that
for all \(t>t_0\). From (1.4), we know that \(u_1\) satisfies
where \(Q_1(x,t)=\chi _1\nabla \cdot \textbf{w}_1-E_1(u_1,u_2)\) for \((x,t)\in \Omega \times (t_0,\infty )\). Using (4.2) and (4.4), one has
In view of (4.2) and (4.6), one can apply the interior \(L^{p}\) estimate [28, Theorems 7.22 and 7.35] to (4.5) to obtain
where \(W^{2,1}_q\left( \Omega \times \left[ t_1,t_2\right] \right) :=\left\{ u\mid Du,D^2 u,u_t\in L^q\left( \Omega \times \left[ t_1,t_2\right] \right) \right\} \) for \(t_2>t_1>0\). By taking q appropriately large and using the Sobolev embedding theorem we have
Similarly, it follows that
Using (4.4), (4.7) and (4.8), we obtain that the solution \((\textbf{w}_1,\textbf{w}_2)\) of the elliptic system (2.16) satisfies
Clearly, it follows from (4.7)–(4.9) that
An application of the Schauder estimate to (4.5) shows that
Similarly, we have
In view of (4.10) and (4.11), we can apply Lemma 2.2 to (2.16) to obtain
Noting that the constant \(C(\theta )\) is independent of \(j\ge 0\), we get (4.1) directly from (4.10)-(4.12). \(\square \)
4.1 Weak competition: \(c<\frac{\gamma _1}{\gamma _2}<\frac{1}{b}\)
To proceed, we define the positive constants
under the condition (1.14).
Lemma 4.2
Let \(\eta _0\) and \(\eta \) be defined by (4.13). If \(bc\in (0,1)\) and (1.14) holds, then the positive constants
satisfy
where
and
with
Proof
This proof is straightforward and tedious, and we give the detailed proof in Appendix B. \(\square \)
Now we are in a position to derive the following result.
Lemma 4.3
Let \((u_1, u_2, \textbf{w}_1, \textbf{w}_2)\) be the global classical solution of (1.4) obtained in Theorem 1.1. Assume \(c<\frac{\gamma _1}{\gamma _2}<\frac{1}{b}\) and let \((u_{1}^*,u_{2}^*)\) be defined in (1.8). If (1.13) or (1.14) holds, then there exist positive constants \(\Gamma _1\) and \(\Gamma _2\) such that the energy functional
satisfies
and
for a positive constant \(\theta _1\), where
Proof
By the symmetry of the equations satisfied by \(u_1\) and \(u_2\) in (1.4), we only need to prove the conclusion under the condition (1.14). In the rest of this proof, we let the positive constants \(\Gamma _1\) and \(\Gamma _2\) be given by Lemma 4.2.
We first prove (4.15). Define the function \(\psi (s):=s-u_1^*-u_1^*\ln \frac{s}{u_1^*}\) for \(s>0\), then \(\psi '(s)=1-\frac{{u_1^*}}{s}\) with \(\psi '({u_1^*})=0\) and \(\psi ''(s)=\frac{{u_1^*}}{s^2}>0\). Hence we have \(\psi (s)\ge \psi ({u_1^*})=0\) for \(s>0\), which implies \( u_1-u_1^*-u_1^*\ln \frac{u_1}{u_1^*}\ge 0. \) Similar arguments for \(u_2\) yield \( u_2-u_2^*-u_2^*\ln \frac{u_2}{u_2^*}\ge 0. \) Therefore, (4.15) is proved. It remains to prove (4.16). To this end, we multiply the first equation in (1.4) by \({1-\frac{u_1^*}{u_1}}\), integrate the resulting equation by parts along with the boundary conditions in (1.4) and use \(\gamma _1-{u_1^*}-c{u_2^*}=0\) to get
for all \(t>0\). Similarly, it holds that
for all \(t>0\). As deriving (3.7), by Young’s inequality we can obtain
which implies
Similarly, we can obtain
For \(\eta \) given by (4.13), the combination of (4.18)–(4.21) shows that
where \(X_{1}:=\left( u_1-u_{1}^{*}, u_2-u_{2}^{*}\right) \), \(Y_{1}:=\left( \frac{\nabla u_1}{u_1}, \frac{\nabla u_2}{u_2}, \textbf{w}_1, \textbf{w}_2\right) \) and \(A_{1}, B_{1}\) are matrices denoted by
We next prove that the matrices \(A_1\) and \(B_1\) are both positive definite. Denoting the determinant of a general square matrix X by |X| and denote the upper left k-by-k (\(k=1,2,3\)) corner of \(B_1\) by \(B_1^{(k)}\), then by (4.14) we have \(|B_1^{(1)}|=d_1 \Gamma _2 {u_1^*}>0\), \(|B_1^{(2)}|=d_1 d_2 \Gamma _2\Gamma _1{u_1^*}{u_2^*}>0\),
and
Sylvester’s criterion thus entails that the matrix \(B_1\) is positive definite. For the matrix \(A_1\), we know from (4.14) that \(\Gamma _2 - b^2-\eta >0\) and
where the function \(\psi _1\) is defined in Lemma 4.2. Again, it follows from Sylvester’s criterion that the matrix \(A_1\) is positive definite. Therefore, we can find a positive constant \(\theta _1\) such that
The combination of (4.17), (4.22) and (4.23) proves (4.16). \(\square \)
With Lemmas 2.5, 4.1 and 4.3, we can use a similar argument as in the proof of [42, Lemma 3.4] to prove the following result.
Lemma 4.4
Under the conditions of Lemma 4.3, for any \(\theta \in (0,1)\), it holds that
Proof
Let \(\mathcal E_{1}(t), \mathcal F_{1}(t)\) be given in Lemma 4.3. Clearly, \(\mathcal E_{1}(t)\) is bounded from below according to (4.15). Thanks to Lemma 4.1, it can be seen that \(\mathcal F_{1}(t) \in C^{\theta / 2}([1, \infty ))\) and \(\left\| \mathcal F_{1}\right\| _{C^{\theta / 2}([1, \infty ))} \le k\) in \([1, \infty )\) for some \(k>0\). In view of (4.16), we can apply Lemma 2.5 to deduce \(\lim _{t \rightarrow \infty }\mathcal F_{1}(t)=0\). That is
Take \(0<\theta<\theta ^{\prime }<1.\) According to Theorem 2.1, in the space \(C^{2+\theta ^{\prime }}(\bar{\Omega })\), \(u_1(\cdot , t)\) and \(u_2(\cdot , t)\) are bounded for \(t \ge 1.\) Using the compact arguments and the uniqueness of limits (cf. [42, (3.12)], see also [20, Remark 6.2]) we can show that
Using (4.20), (4.21) and (4.24), one has
This together with (4.1), the compact arguments and the uniqueness of limits shows that
which along with (4.24) completes the proof. \(\square \)
We are now in a position to investigate the convergence rate.
Lemma 4.5
Under the conditions of Lemma 4.3. There exist two constants \(\sigma >0\) and \(C>0\) independent of t such that
holds for all \(t>T_0\) with some \(T_0>1\), where \(u_{1}^*\) and \(u_{2}^*\) are given by (1.8).
Proof
With Lemmas 4.3 and 4.4, one can use a similar argument as in the proof of [44, Lemma 3.7] (where the \(L^\infty (\Omega )\) decay rate are obtained) to obtain that there exist positive constants \(\sigma _1\) and \(T_0\) such that
For the convenience of readers, we shall sketch the proof of (4.26). In view of Lemma 4.4, we can apply L’Hôpital’s rule to derive that
which by the continuity yields a constant \(T_0>1\) such that
for all \(t\ge T_0\). Then, it follows from the definition of \(\mathcal {E}_{1}(t)\) and \(\mathcal {F}_{1}(t)\) that
which together with (4.16) implies
Solving the above inequality, we obtain
By the definition of \(\mathcal {E}_{1}(t)\) and \(\mathcal {F}_{1}(t)\) and (4.27), one can find a constant \(C_{3}>0\) such that
which along with (4.28) shows that
The combination of (4.1), (4.29) and the Gagliardo–Nirenberg inequality
yields (4.26) by choosing \(C_1\) large enough and taking \(\sigma _1=\frac{\theta _{1}}{10 C_{2}}\).
In view of (4.20) and (4.21), it follows from (4.26) immediately that
With (4.1) and (4.31), we can use a similar argument as deriving (4.30) to show that
where \(\sigma _2=\frac{\sigma _1}{5}\). Therefore, (4.25) is a direct consequence of (4.26) and (4.32) by taking C appropriately large and \(\sigma =\sigma _2\). The proof is completed. \(\square \)
4.2 Competitive exclusion: \(\frac{\gamma _1}{\gamma _2}<\min \{\frac{1}{b},c\}\)
As the results stated for the weak competition case in the above subsection, we have the following conclusions.
Lemma 4.6
Let \((u_1, u_2, \textbf{w}_1, \textbf{w}_2)\) be the global classical solution of (1.4) obtained in Theorem 1.1. Assume \(\frac{\gamma _1}{\gamma _2}<\min \{\frac{1}{b},c\}\) and (1.15) holds. Define two constants
where the function f is given by (1.9). Then
Moreover, the energy functional
satisfies \(\mathcal E_2(t)\ge 0\) for all \(t>0\), and
for a positive constant \(\theta _2\), where
Proof
First of all, by a similar argument as proving (4.15), we can obtain \(\mathcal E_2(t)\ge 0\) for all \(t>0\). We then prove (4.34). Using \(\gamma _2-b\gamma _1>0\) and (1.15), we obtain the first inequality in (4.34) directly, moreover, we have
which proves the second inequality in (4.34).
It remains to prove (4.36). Integrating the first two equations of (1.4) by parts with \(\nabla u_{1} \cdot \textbf{n} \mid _{\partial \Omega }=\textbf{w}_1 \cdot \textbf{n} \mid _{\partial \Omega }=0\) and using \(\frac{\gamma _1}{\gamma _2}<c\), we have
As deriving (4.19), for all \(t>0\), we have
It follows from (4.21), (4.35), (4.38), (4.39) and Young’s inequality that
where \(X_{2}=\left( u_1, u_2-\gamma _2\right) \), \(Y_{2}=\left( \frac{\nabla u_2}{u_2},\textbf{w}_2\right) \) and \(A_{2}, B_{2}\) are matrices denoted by
Using \(\gamma _2-b\gamma _1>0\), (1.15), (4.33) and (4.34), we obtain \(\Gamma _4 - b^2 >0\) and
Moreover, it is obvious that \(d_2 \gamma _2 \Gamma _3>0\), and by (4.34) we have
In view of Sylvester’s criterion, it follows from (4.41) and (4.42) that the matrices \(A_2\) and \(B_2\) are positive definite, and hence we can find a positive constant \(\theta _2\) such that
which along with \(X_{2}=\left( u_1, u_2-\gamma _2\right) \), (4.37) and (4.40) proves (4.36). The proof is completed. \(\square \)
Lemma 4.7
Under the conditions of Lemma 4.6, there exists a constant \(T_1>0\) such that
for all \(t>T_1\), where C is a positive constant independent of t.
Proof
First, by a similar argument as in the proof of Lemma 4.4, one can obtain
Recalling the definitions of \(\mathcal E_2(t)\) and \(\mathcal F_2(t)\), and using (4.27) and Hölder’s inequality, we can find some \(T_1>0\) such that
which together with (4.36) gives that
Solving the above ordinary differential inequality, we arrive at
The rest of the proof can follow similar arguments as in the proof of Lemma 4.5 and we omit it for brevity. \(\square \)
Proof of Theorem 1.2.
The assertions in (i) and (ii) of Theorem 1.2 result from Lemma 4.5 and Lemma 4.7, respectively. The assertions in (iii) are essentially similar to those in (ii) and can be proved by simply swapping \(u_1, b,\gamma _1\) with \(u_2, c,\gamma _2\), respectively, in the proof of (ii). \(\square \)
Data availability
Not applicable.
References
Averill, I., Lam, K.-Y., Lou, Y.: The role of advection in a two-species competition model: a bifurcation approach, vol. 245. Mem. Amer. Math. Soc., (2017)
Averill, I., Lou, Y., Munther, D.: On several conjectures from evolution of dispersal. J. Biol. Dyn. 6(2), 117–130 (2012)
Bourguignon, J.P., Brezis, H.R.: Remarks on the Euler equation. J. Funct. Anal. 15, 341–363 (1974)
Brown, P.N.: Decay to uniform states in ecological interactions. SIAM J. Appl. Math. 38(1), 22–37 (1980)
Robert, S.: Cantrell and Chris Cosner. Spatial ecology via reaction-diffusion equations, John Wiley & Sons Ltd, Chichester (2003)
Cantrell, R.S., Cosner, C., Lou, Y.: Movement toward better environments and the evolution of rapid diffusion. Math. Biosci. 204(2), 199–214 (2006)
Cantrell, R.S., Cosner, C., Lou, Y.: Advection-mediated coexistence of competing species. Proc. Roy. Soc. Edinb. A 137(3), 497–518 (2007)
Cantrell, R.S., Cosner, C., Lou, Y.: Evolution of dispersal and the ideal free distribution. Math. Biosci. Eng. 7(1), 17 (2010)
Chen, X., Hambrock, R., Lou, Y.: Evolution of conditional dispersal: a reaction-diffusion-advection model. J. Math. Biol. 57(3), 361–386 (2008)
Cioranescu, D., Dias, J.-P.: A time dependent coupled system related to the tridimensional equations of a nematic liquid crystal. J. Math. Anal. Appl. 73(1), 252–266 (1980)
Cosner, C.: Reaction–diffusion–advection models for the effects and evolution of dispersal. Discret. Contin. Dyn. Syst. 34(5), 1701–1745 (2014)
Dias, J.-P.: Un problème aux limites pour un système d’équations non linéaires tridimensionnel. Boll. Un. Mat. Ital. B (5) 16(1), 22–31 (1979)
Fisher, R.A.: The wave of advance of advantageous genes. Ann. Eugen. 7(4), 355–369 (1937)
Gejji, R., Lou, Y., Munther, D., Peyton, J.: Evolutionary convergence to ideal free dispersal strategies and coexistence. Bull. Math. Biol. 74(2), 257–299 (2012)
Grindrod, P.: Models of individual aggregation or clustering in single and multi-species communities. J. Math. Biol. 26(6), 651–660 (1988)
Grindrod, P.: Patterns and Waves. The Clarendon Press, Oxford University Press, New York (1991)
Grisvard, P.: Elliptic problems in nonsmooth domains, volume 69 of Classics in Applied Mathematics. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, (2011)
He, X., Ni, W.M.: Global dynamics of the Lotka-Volterra competition-diffusion system: diffusion and spatial heterogeneity I. Commun. Pure Appl. Math. 69(5), 981–1014 (2016)
Holmes, E.E., Lewis, M.A., Banks, J.E., Veit, R.R.: Partial differential equations in ecology: spatial interactions and population dynamics. Ecology 75(1), 17–29 (1994)
Hu, B.: Blow-up Theories for Semilinear Parabolic Equations, vol. 2018 of Lecture Notes in Mathematics. Springer, Heidelberg, (2011)
Ibrahim, H., Nasreddine, E.: Traveling waves for a model of individual clustering with logistic growth rate. J. Math. Phys. 58(8), 081505 (2017)
Jin, C.: Global classical solution and stability to a coupled chemotaxis-fluid model with logistic source. Discret. Contin. Dyn. Syst. 38(7), 3547–3566 (2018)
Jüngel, A.: Diffusive and nondiffusive population models. In Mathematical modeling of collective behavior in socio-economic and life sciences, pp. 397–425. Springer, (2010)
Kareiva, P., Odell, G.: Swarms of predators exhibit “preytaxis” if individual predators use area-restricted search. Am. Nat. 130(2), 233–270 (1987)
Kondo, S., Miura, T.: Reaction-diffusion model as a framework for understanding biological pattern formation. Science 329(5999), 1616–1620 (2010)
Krause, A.L., Van Gorder, R.A.: A non-local cross-diffusion model of population dynamics II: exact, approximate, and numerical traveling waves in single- and multi-species populations. Bull. Math. Biol. 82(8), 113 (2020)
Kurowski, L., Krause, A.L., Mizuguchi, H., Grindrod, P., Van Gorder, R.A.: Two-species migration and clustering in two-dimensional domains. Bull. Math. Biol. 79(10), 2302–2333 (2017)
Gary, M.: Lieberman. Second order parabolic differential equations, World Scientific Publishing Co., Inc, River Edge, NJ (1996)
Lou, Y., Lutscher, F.: Evolution of dispersal in open advective environments. J. Math. Biol. 69(6), 1319–1342 (2014)
Lou, Y., Ni, W.-M.: Diffusion, self-diffusion and cross-diffusion. J. Differ. Equ. 131(1), 79–131 (1996)
Lou, Y., Zhou, P.: Evolution of dispersal in advective homogeneous environment: the effect of boundary conditions. J. Differ. Equ. 259(1), 141–171 (2015)
Mora, X.: Semilinear parabolic problems define semiflows on \(C^{k}\) spaces. Trans. Am. Math. Soc. 278(1), 21–55 (1983)
Murray, J.D.: Mathematical Biology I: An introduction, vol. 17 of Interdisciplinary Applied Mathematics. Springer-Verlag, New York, third edition, (2002)
Nasreddine, E.: Well-posedness for a model of individual clustering. Discret. Contin. Dyn. Syst. Ser. B 18(10), 2647–2668 (2013)
Nasreddine, E.: A model of individual clustering with vanishing diffusion. Asymptot. Anal. 88(1–2), 93–110 (2014)
Nasreddine, E.: Two-dimensional individual clustering model. Discret. Contin. Dyn. Syst. Ser. S 7(2), 307–316 (2014)
Rowell, J.T.: The limitation of species range: a consequence of searching along resource gradients. Theor. Popul. Biol. 75(2–3), 216–227 (2009)
Schoenauer, M.: Quelques résultats de régularité pour un systéme elliptique avec conditions aux limites couplées. Ann. Fac. Sci. Toulouse Math. 2(2), 125–135 (1980)
Sherratt, J.A., Murray, J.D.: Models of epidermal wound healing. Proc. R. Soc. Lond. B 241(1300), 29–36 (1990)
Taylor, N.P., Kim, H., Krause, A.L., Van Gorder, R.A.: A non-local cross-diffusion model of population dynamics I: emergent spatial and spatiotemporal patterns. Bull. Math. Biol. 82(8), 112 (2020)
Volpert, V., Petrovskii, S.: Reaction-diffusion waves in biology. Phys. Life Rev. 6(4), 267–310 (2009)
Wang, J., Wang, M.: The dynamics of a predator-prey model with diffusion and indirect prey-taxis. J. Dyn. Differ. Equ. 32(3), 1291–1310 (2020)
Wang, M.: Note on the Lyapunov functional method. Appl. Math. Lett. 75, 102–107 (2018)
Wang, Z.-A., Xu, J.: On the Lotka-Volterra competition system with dynamical resources and density-dependent diffusion. J. Math. Biol. 82(1–2), 37 (2021)
Winder, L., Alexander, C.J., Holland, J.M., Woolley, C., Perry, J.N.: Modelling the dynamic spatio–temporal response of predators to transient prey patches in the field. Ecol. Lett. 4(6), 568–576 (2001)
Winkler, M.: Aggregation versus global diffusive behavior in the higher-dimensional Keller–Segel model. J. Differ. Equ. 248(12), 2889–2905 (2010)
Yi, F., Wei, J., Shi, J.: Bifurcation and spatiotemporal patterns in a homogeneous diffusive predator-prey system. J. Differ. Equ. 246(5), 1944–1977 (2009)
Zhou, P., Tang, D., Xiao, D.: On lotka-volterra competitive parabolic systems: exclusion, coexistence and bistability. J. Differ. Equ. 282, 596–625 (2021)
Zhou, P., Xiao, D.: Global dynamics of a classical Lotka–Volterra competition-diffusion-advection system. J. Funct. Anal. 275(2), 356–380 (2018)
Peng, R., Wu, C.-H., Zhou, M.: Sharp estimates for the spreading speeds of the Lotka-Volterra diffusion system with strong competition. Ann. Inst. H. Poincaré C Anal. Non Linéaire 38(3), 507–547 (2021)
Acknowledgements
The authors are very thankful to the anonymous referee for the constructive comments, which help us improve the exposition of this paper. The research of W. Tao was partially supported by NSFC No. 12201082, PolyU Postdoc Matching Fund Scheme Project ID P0030816/B-Q75G, 1-W15F and 1-YXBT. The research of Z.-A. Wang was partially supported by Hong Kong RGC GRF grant No. PolyU 15307222 and Postdoc Matching Fund Scheme Project ID P0034904 (Primary Work Programme W15F). and Project ID P0045702 (Primary Work Programme 1-YXBT). The research of W. Yang was partially supported by National Key R &D Program of China 2022YFA1006800, NSFC No. 12171456, No. 12271369 and SRG2023-00067-FST.
Funding
Open access funding provided by The Hong Kong Polytechnic University
Author information
Authors and Affiliations
Contributions
Each of the authors has reviewed the manuscript and made equal contributions to this paper.
Corresponding author
Ethics declarations
Conflict of interest
The author declares no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A
In this section, we consider the regularity of the vector field \(\textbf{w}\) satisfying:
where \(\Omega \subset \mathbb {R}^{n}\), \(n\in \left\{ 2,3\right\} \), is a bounded domain with a smooth boundary and \(\textbf{f} \in \left( L^{p}(\Omega )\right) ^{n}\) for some \(1<p<\infty \). Then the following regularity result holds.
Lemma A1
If \(\textbf{f} \in \left( L^{2}(\Omega )\right) ^{n}\), then the problem (A1) has a unique solution \(\textbf{w}\in (H^2(\Omega ))^n\) and there is a positive constant \(C(\Omega )\) depending only on \(\Omega \) such that
Proof
The existence and uniqueness of the solution \(\textbf{w}\in (H^{2}(\Omega ))^n\) to (A1) is stated in Lemma 2.2. Next we prove the regularity. We only give the details for \(n=3\), and the proof for \(n=2\) is similar and simpler. We divide the proof into two steps.
Step 1. We prove the following estimate for a positive constant C,
Multiplying the i-th component (\(i=1,2,3\)) of the first equation in (A1) by \( w_i\) and integrating the resulting equation by parts, we get
which gives
Noticing the boundary condition implies
we get (A2) by the Cauchy-Schwarz inequality: \(\int _\Omega \textbf{w}\cdot \textbf{f}dx\le \frac{1}{2}\Vert \textbf{w}\Vert _{L^{2}(\Omega )}^2+\frac{1}{2}\Vert f\Vert _{L^{2}(\Omega )}^2\).
Step 2. Suppose \(\{\textbf{n},\varvec{\tau }_1,\varvec{\tau }_2\}\) constitutes the Frenet coordinate associated with the boundary \(\partial \Omega \). By assuming the domain is sufficiently smooth, we can extend \(\{\textbf{n},\varvec{\tau }_1,\varvec{\tau }_2\}\) to a \(C^\infty \) function defined in \(\Omega \) such that their \(C^2\) norms are uniformly bounded and any two of them are orthogonal to each other, still denoted by \(\{\textbf{n},\varvec{\tau }_1,\varvec{\tau }_2\}\).
Now we shall estimate the \(H^2\)-norm of \(\textbf{w}\cdot \textbf{n}\), \(\textbf{w}\cdot \varvec{\tau }_1\) and \(\textbf{w}\cdot \varvec{\tau }_2\) in the following. We start with \(\textbf{w}\cdot \textbf{n}\) which satisfies
Therefore, we have from (A1) that
We denote the right hand side of the first equation in (A3) by \(\tilde{\textbf{f}}_1\). Using the classical elliptic regularity estimate, along with the boundary condition and the conclusion in Step 1, we get
Concerning \(\textbf{w}\cdot \varvec{\tau }_1\), we have
where the boundary condition holds since
By the trace theorem and the conclusion in Step 1, we have
On the other hand, by denoting the right hand side in the first equation of (A5) by \(\tilde{\textbf{f}}_2\), it is easy to see that \(\Vert \tilde{\textbf{f}}_2\Vert _{L^2(\Omega )}\le C(\Omega )\Vert \textbf{f}\Vert _{L^2(\Omega )}\). By the results of [17, Section 2.3], we have
Similarly, we have
Collecting (A4), (A6) and (A7), we arrive at
Hence the proof is completed. \(\square \)
Lemma A2
If \(\textbf{f} \in \left( H^{2}(\Omega )\right) ^{n}\), then the system (A1) has a unique solution \(\textbf{w}\in (H^4(\Omega ))^n\) and there is a positive constant \(C(\Omega )\) depending only on \(\Omega \) such that
Proof
We consider the regularity of solutions to (A1) for \(n=3\) only, and the case for \(n=2\) can be proved similarly. Defining the Frenet coordinate system \(\{\textbf{n},\varvec{\tau }_1,\varvec{\tau }_2\}\) and taking differentiation of (A1) with respect to \(x_k\), \(k\in \{1,2,3\}\), we have
Next, we estimate the functions \(\textbf{w}_{x_k}\cdot \textbf{n},~\textbf{w}_{x_k}\cdot \varvec{\tau }_1\) and \(\textbf{w}_{x_k}\cdot \varvec{\tau }_2\). By direct computations, we get
Denote the right hand side of (A9) by \(\tilde{\textbf{f}}_3\). Using Lemma A1, we see that
By the classical elliptic regularity, we have
Concerning \(\textbf{w}_{x_k}\cdot \varvec{\tau }_1\), we have
Denoting the right hand side in the first equation of (A11) by \(\tilde{\textbf{f}}_4\), we can use Lemma A1 to get that
From the last two equations in (A8), we notice that on \(\partial \Omega \),
From (A13) we get
As a consequence of (A14), we have
Then it is easy to see that
With (A12) and (A15), the results of [17, Section 2.3] entail that
Similarly, we have
Combining the above two estimates with (A10), we get
Now we derive the higher regularity based on the assumption that \(\textbf{f}\in H^2(\Omega )\). Differentiating (A1) with respect to \(x_j\) and \(x_k\), \(j,k\in \{1,2,3\}\), we have
Next, we estimates the terms \(\textbf{w}_{x_j x_k}\cdot \textbf{n},~\textbf{w}_{x_j x_k}\cdot \varvec{\tau }_1\) and \(\textbf{w}_{x_j x_k}\cdot \varvec{\tau }_2\). Direct computations give us that
Denote the right hand side of the first and second equations of (A18) by \(\tilde{\textbf{f}}_5\) and \(\tilde{\textbf{f}}_6\), respectively. Using (A16), we see that
and
By the classical elliptic regularity, we have
Concerning \(\textbf{w}_{x_j x_k}\cdot \varvec{\tau }_1\), we find it satisfies
Denoting the right hand side in the first equation of (A11) by \(\tilde{\textbf{f}}_7\) and using (A15), we get
From the last equation in (A17), we have
which yields
As a consequence of (A20), we have
Then it is easy to see that
With (A21) and (A22), we use the results of [17, Section 2.3] again and get that
Similar procedures give
Combining the above two estimates with (A19), we get
which along with (A16) completes the proof. \(\square \)
Appendix B
In this section, we give the proof of Lemma 4.2.
Proof of Lemma 4.2
It follows from \(\eta >0\),
that \(\beta :=\eta _0f(b,c)+\left( 1-\eta _0\right) \frac{K_2}{{u_2^*}}<\frac{K_2}{{u_2^*}}\) satisfies
Moreover, it holds that
Thus the inequality satisfied by \(\Gamma _1\) in (4.14) is proved. We next prove the inequalities satisfied by \(\Gamma _2\) in (4.14). By (B1) and (B2), we have
Using (1.11), (1.14) and (4.13), we obtain
Clearly,
We deduce from (B5) and (B6) that
Since \({\Gamma _2}_*\) and \(\Gamma _2^*\) are two zeros of \(\psi _1(s)=-\frac{c^2}{4}\,s^2+\alpha _1 s+\alpha _2\) for \(s>0\), by (B7) we have \(\psi _1(\Gamma _2)>0\). It remains to prove \(\Gamma _2>b^2+\eta \). Indeed, we have
which along with (B7) and (B8) shows that \(\Gamma _2>{\Gamma _2}_*\ge b^2+\eta \), and hence the proof is completed. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tao, W., Wang, ZA. & Yang, W. Global dynamics of a two-species clustering model with Lotka–Volterra competition. Nonlinear Differ. Equ. Appl. 31, 47 (2024). https://doi.org/10.1007/s00030-024-00934-7
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00030-024-00934-7