A robust alternative to examine data dependency of fixed points of quasi-contractive operators: an efficient approach that relies on the collage theorem

Abstract

Usurelu et al. (Int J Comput Math 98:1049–1068, 2021) presented stability and data dependence results for a TTP (Thakur–Thakur–Postolache) iteration algorithm associated with quasi-strictly contractive mappings and contraction mappings, respectively, but these results were subject to strong conditions on the parametric control sequences used in the TTP iteration algorithm. This article aims to expand those results conducting a thorough analysis of the convergence of TTP and S iteration algorithms and improve those results by removing the restrictions on the parametric control sequences. Additionally, a data dependence result for the TTP iteration algorithm of quasi-strictly contractive mappings is established and several collage theorems are introduced to offer new insights into the data dependence of fixed points of quasi-strictly contractive mappings and to solve related inverse problems. In order to exhibit the dependability and effectiveness of all the results discussed in this work, a multitude of numerical examples are furnished, encompassing both linear and nonlinear differential equations (DEs) and partial differential equations (PDEs). This work can be viewed as an important refinement and complement to the study by Usurelu et al. (Int J Comput Math 98:1049–1068, 2021).

1 Introduction and preliminaries

Due to the inherent non-linearity of nature, scientists in different fields come across unique nonlinear problems specific to their research areas. Such problems can be modeled as nonlinear operator equations:

$$\begin{aligned} \text {Find }r^{*}\in \mathbb {X}\text { such that }\mathbb {T}r^{*}=r^{*}\text {,} \end{aligned}$$

(1)

in which $\mathbb {X}$ is an underlying space and $\mathbb {T}$ is an appropriate self-map of $\mathbb {X}$. Solving problems of this type, also known as fixed point equations, is essentially the same as identifying the fixed points of the corresponding mapping $\mathbb {T}$. For example, the solution of one dimensional Bratu’s nonlinear boundary value problem:

$$\begin{aligned} -r^{\prime \prime }\left( \tau \right) =\lambda \exp (r\left( \tau \right) ) \text {, }r\left( 0\right) =0\text {, }r\left( 1\right) =0\text {, }\tau \in \left[ 0,1\right] \text {, }\lambda >0\text {,} \end{aligned}$$

is equivalent to finding the fixed point of an operator $\mathbb {T}_{\mathbb { G}}:C\left[ 0,1\right] \rightarrow C\left[ 0,1\right]$ defined by $\mathbb {T }_{\mathbb {G}}\left( r\right) =-\int \limits _{0}^{1}\mathbb {G}\left( w,\tau \right) \lambda \exp (r\left( w\right) )dw$ in which $\mathbb {G}\left( w,\tau \right)$ is the Green function defined by $\mathbb {G}\left( w,\tau \right) =w\left( 1-\tau \right)$, $w\in \left[ 0,\tau \right]$ and $\mathbb {G}\left( w,\tau \right) =\tau \left( 1-w\right)$, $w\in \left[ \tau ,1\right]$ (see, e.g., Kafri and Khuri 2016). In general, the mapping $\mathbb {T}$ in (1) is required to meet specific contractive conditions to allow the use of fixed point method in finding solutions of (1) (i.e., fixed points of $\mathbb {T}$). Therefore, it is crucial to investigate the classes of mappings that fulfill different contractive conditions since they play a significant role in studying fixed points. We shall recall a few of them in the following to make the reading easier to follow.

Henceforth, $\emptyset \ne \mathbb {S}$ denotes a convex and closed subset of an arbitrary Banach space $\mathbb {B}$ equipped with norm $\left\| \cdot \right\|$, in which $\mathbb {N}$ stands for the set of non-negative integers, and $\mathbb {F}_{\mathbb {T}}$ denotes the set of points $r^{*}$ such that $\mathbb {T}r^{*}=r^{*}$.

Definition 1

Recall that a mapping $\mathbb {T}:\mathbb {S\rightarrow S}$ is said to be

• (i) a contraction if there exists a constant $K\in \left[ 0,1\right)$ such that $\left\| \mathbb {T}r_{1}-\mathbb {T}r_{2}\right\| \le K\left\| r_{1}-r_{2}\right\|$ for all $r_{1},r_{2}\in \mathbb {S}$,

• (ii) a non-expansive if $\left\| \mathbb {T}r_{1}-\mathbb {T} r_{2}\right\| \le \left\| r_{1}-r_{2}\right\|$ for all $r_{1},r_{2}\in \mathbb {S}$,

• (iii) a quasi-strictly contractive with $r^{*}\in$ $\mathbb {F}_{\mathbb {T}}$ if there exists a constant $K\in \left[ 0,1\right)$ such that $\left\| \mathbb {T}r-r^{*}\right\| \le K\left\| r-r^{*}\right\|$ for all $r\in \mathbb {S}$.

Clearly, a contraction mapping with a fixed point $r^{*}$ is a quasi-strictly contractive mapping. However, the converse of this fact is not true as shown below.

Example 1

Let $\mathbb {S}=\left[ -0.5,1\right]$ be endowed with the usual metric. Define a mapping $\mathbb {T}:\mathbb {S\rightarrow S}$ by $\mathbb {T} r=-r^{2}+r+0.5$. An easy computation yields that $r^{*}=1/\sqrt{2}$ is the unique fixed point of $\mathbb {T}$ in $\mathbb {S}$. Now, suppose that $\mathbb {T}$ is a contraction mapping. Then, there must be a constant $K\in \left[ 0,1\right)$ such that

$$\begin{aligned} \left| \mathbb {T}r_{1}-\mathbb {T}r_{2}\right|= & {} \left| -r_{1}^{2}+r_{1}+r_{2}^{2}-r_{2}\right| \nonumber \\= & {} \left| r_{1}-r_{2}\right| \left| 1-\left( r_{1}+r_{2}\right) \right| \nonumber \\\le & {} K\left| r_{1}-r_{2}\right| \text {, }\forall r_{1},r_{2}\in \mathbb {S}. \end{aligned}$$

(2)

WLOG, suppose that $r_{1}\ne r_{2}$. Then, inequality (2) implies that

$$\begin{aligned} \left| 1-\left( r_{1}+r_{2}\right) \right| \le K. \end{aligned}$$

(3)

If we take $r_{1}=-0.5$ and $r_{2}=0.5$ in (3), then we attain $1\le K$, a contradiction. Thus, $\mathbb {T}$ is not a contraction mapping.

Now, we shall show that $\mathbb {T}$ is a quasi-strictly contractive mapping. For all $r\in \mathbb {S}$, we have

$$\begin{aligned} 1.5-1/\sqrt{2}\ge 1-\left( r+1/\sqrt{2}\right) \ge -1/\sqrt{2} \end{aligned}$$

which gives

$$\begin{aligned} 1.5-1/\sqrt{2}\ge 1-\left( r+1/\sqrt{2}\right) \ge -\left( 1.5-1/\sqrt{2} \right) \text {,} \end{aligned}$$

or

$$\begin{aligned} 1.5-1/\sqrt{2}\ge \left| 1-\left( r+1/\sqrt{2}\right) \right| \text { .} \end{aligned}$$

(4)

By using (4), we obtain

$$\begin{aligned} \left| \mathbb {T}r-r^{*}\right|= & {} \left| -r^{2}+r+0.5-1/ \sqrt{2}\right| \\= & {} \left| r-1/\sqrt{2}\right| \left| 1-\left( r+1/\sqrt{2} \right) \right| \\\le & {} \left( 1.5-1/\sqrt{2}\right) \left| r-1/\sqrt{2}\right| \text {, }\forall r\in \mathbb {S}\text {.} \end{aligned}$$

Hence, $\mathbb {T}$ is a quasi-strictly contractive mapping for any $K\in \left[ 1.5-1/\sqrt{2},1\right)$.

The versatile utility of quasi-strictly contractive mappings in the study of fixed points has been uncovered (Hacıoğlu 2021; Erturk and Gursoy 2019; Gursoy et al. 2020; Berinde and Păcurar 2006; Karaca et al. 2017). Although Bosede and Rhoades (2010) are sometimes credited as the originators of this concept in some research, it is the responsibility of the relevant researchers to recognize Schezer (1995) as the actual creator of this idea. Now, let’s gather some information about quasi-strictly contractive mappings.

Remark 1

If $\mathbb {T}$ is a quasi-strictly contractive mapping with $r^{*}\in$ $\mathbb {F}_{\mathbb {T}}$ and contractivity factor $K\in \left[ 0,1\right)$ and $\widetilde{\mathbb {T}}:\mathbb {S\rightarrow S}$ is a mapping, then we have

$$\begin{aligned} \left\| \mathbb {T}r_{1}-\mathbb {T}r_{2}\right\| \le K\left\| r_{1}-r_{2}\right\| +2K\left\| r_{2}-r^{*}\right\| \text {, } \forall r_{1},r_{2}\in \mathbb {S}\text {,} \end{aligned}$$

(5)

and

$$\begin{aligned} \left\| \mathbb {T}r_{1}-\widetilde{\mathbb {T}}r_{2}\right\| \le K\left\| r_{1}-r_{2}\right\| +2K\left\| r_{1}-r^{*}\right\| +\left\| \mathbb {T}r_{2}-\widetilde{\mathbb {T}}r_{2}\right\| \text {, } \forall r_{1},r_{2}\in \mathbb {S}\text {.} \end{aligned}$$

(6)

Inequalities (5) and (6) was obtained in (Gursoy et al. 2019, Remark 1.3. (ii)) and (Erturk and Gursoy 2019, Lemma 2.1), respectively.

There are various systematic methods available in the field, known as direct and iterative methods, for solving equations in the format of (1). Direct methods are typically insufficient when it comes to solving nonlinear equations, which leaves iteration algorithms as the only available mathematical tools to solve such equations. Despite the fact that the study of fixed-point iteration algorithms began with the renowned Picard iteration (Picard 1890), which is commonly employed to estimate fixed points of contraction mappings, the initial research on such algorithms dates back to the 1st century AD, see (Chabert and Barbin 1999). It is well-known that the Picard iteration is inadequate for approximating the solutions of certain operator equations associated with non-expansive or non-contraction mappings. Therefore, Krasnoselskii (1955), Mann (1953), and Ishikawa (1974) iteration algorithms have been developed to tackle with these equations and have been extensively researched by various scholars within different mathematical contexts. Drawing inspiration from the success of classical iteration algorithms such as Picard, Krasnoselskii, Mann, and Ishikawa, numerous iteration algorithms have been formulated, demonstrating superior performance in addressing various problem-solving tasks. Researchers have conducted in-depth analyses of these algorithms’ qualitative characteristics, including their data dependency, stability, and comparison of convergence performances (see Uddin et al. 2020; Erturk et al. 2017; Gursoy et al. 2016, 2019; Hacıoğlu et al. 2021; Gursoy et al. 2019; Kumar et al. 2020). As the application areas of iteration algorithms continue to expand and diversify, it becomes increasingly important to create new ones or enhance and re-functionalizing existing algorithms if they fail to solve a particular problem. This is a critical task that is always in demand, both in mathematics and applied and computational research domains. To stay up-to-date with the latest developments in iteration algorithms, readers can refer to (Gursoy et al. 2022; Keten Çopur et al. 2021; Maldar 2022a, b; Ali et al. 2022; Bera et al. 2022; Khatoon et al. 2021a, b; Ali and Uddin 2021).

The extensive studies on iterative approximations of fixed points reveals that numerous iteration algorithms can be utilized to tackle diverse problems, but some may perform better than others in achieving the desired level of accuracy under specific conditions. In such cases, it is essential, both in practical and theoretical terms, to opt for an algorithm that exhibits superior convergence speed and computational accuracy for solving the given problem. The concept of stability, coupled with the attribute of superior convergence performance, has emerged as an exceptionally valuable set of mathematical tools. These tools provide an impartial means of evaluating the effectiveness of an iterative algorithm in solving a problem under specific conditions.

Definition 2

(Harder 1987) Let $\mathbb {T}:\mathbb {S}\rightarrow \mathbb {S}$ be a mapping with a fixed point p, $\Psi$ a function, $\left\{ \Phi _{n}^{*}\right\} _{n=0}^{\infty }\subset \mathbb {S}$ an arbitrary sequence, and $\left\{ \Phi _{n}\right\} _{n=0}^{\infty }$ be an iterative sequence defined by $\Phi _{n+1}=\Psi \left( \mathbb {T},\Phi _{n}\right)$, $\forall n\in \mathbb {N}$ for an initial guess $\Phi _{0}\in \mathbb {S}$. Assume that $\left\{ \Phi _{n}\right\} _{n=0}^{\infty }$ converges to p. If $\lim _{n\rightarrow \infty }\left\| \Psi \left( \mathbb {T},\Phi _{n}^{*}\right) -\Phi _{n+1}^{*}\right\| =0\Leftrightarrow \lim _{n\rightarrow \infty }\Phi _{n}^{*}=p$, then one says that $\left\{ \Phi _{n}\right\} _{n=0}^{\infty }$ is stable w.r.t. $\mathbb {T}$.

The superiority of the Picard iteration algorithm over the Mann, Ishikawa, and Noor iteration algorithms in solving operator equations of contraction mappings is a widely known fact. Nonetheless, the Picard iteration algorithm does not exhibit favorable behavior when dealing with non-contraction and non-expansive mappings. In 2007, Agarwal et al. (2007) proposed the following S-iteration algorithm as an alternative that overcomes this limitation of the Picard iteration algorithm and performs better than the Picard, Mann, and Ishikawa iteration algorithms:

Despite having the same convergence performance as the Picard iteration for contraction mappings, this iteration method has gained significant attention from researchers due to its independence from the Mann, Ishikawa, and Noor iteration algorithms, and its ability to outperform these algorithms in terms of speed. Consequently, it has been featured in many research papers and scrutinized in-depth as regards its various properties.

Inspired by S-iteration algorithm, Thakur et al. (2016) proposed the following algorithm:

A recently published paper (Usurelu et al. 2021) has conducted a successful analysis of this iteration algorithm and its various modifications in relation to various aspects such as data dependence, stability, and polynomiography, which refers to an efficient method of encoding some mathematical data through visualization techniques that go beyond creating mere aesthetically pleasing images. To facilitate the readers’ understanding of the discussion, we shall summarize the stability and data dependence findings of (Usurelu et al. 2021) below.

Theorem 1

Let $\mathbb {T},\widetilde{\mathbb {T}}:\mathbb {S}\rightarrow \mathbb {S}$ be two mappings and $\left\{ t_{k_{1}}^{1}\right\} _{k=0}^{\infty }$, $\left\{ \widetilde{t}_{k}^{1}\right\} _{k=0}^{\infty }$ be two sequences generated by TTP iteration algorithm in (8) with real sequences $\left\{ \upsilon _{k}^{i}\right\} _{n=0}^{\infty }\subseteq \left[ 0,1\right] ,i=1,2,3$ associated to $\mathbb {T}$ and $\widetilde{ \mathbb {T}}$, respectively. Suppose that there exists a maximum admissible error $\epsilon >0$ such that $\left\| \mathbb {T}r\mathbb {-}\widetilde{ \mathbb {T}}r\right\| \le \epsilon$, $\forall r\in \mathbb {S}$.

• (i) If $\mathbb {T}$ is a quasi quasi-strictly contractive mapping with a fixed point $r^{*}$ and $\upsilon _{k}^{1}\upsilon _{k}^{2}\upsilon _{k}^{3}\ge a>0$ for all $n\in \mathbb {N}$. Then TTP iteration algorithm is $\mathbb {T-}$stable.

• (ii) If $\mathbb {T}$ is a contraction mapping with a fixed point $r^{*}$ , $\widetilde{\mathbb {T}}\widetilde{r}^{*}=\widetilde{r}^{*}$, $\lim _{k\rightarrow \infty }t_{k}^{1}=r^{*}$, $\lim _{k\rightarrow \infty } \widetilde{t}_{k}^{1}=\widetilde{r}^{*}$, and $\upsilon _{k}^{1}\upsilon _{k}^{2}\upsilon _{k}^{3}\ge \frac{1}{2}$ for all $n\in \mathbb {N}$, then

$$\begin{aligned} \left\| r^{*}-\widetilde{r}^{*}\right\| \le \frac{7\epsilon }{ \left( 1-K\right) ^{2}}\text {,} \end{aligned}$$

(9)

in which $K\in \left[ 0,1\right)$ is the contractivity factor of $\mathbb {T}$.

In this work, we have organized our efforts in the following manner: In Sect. 2 we have conducted a thorough analysis of the convergence of iteration algorithms (7) and (8) applied to quasi-strictly contractive mappings. In Sect. 3 we have utilized the findings of this analysis to enhance and broaden the stability and data dependence results presented in Theorem 1, eliminating the limitations imposed on the parametric sequences utilized in the aforementioned iteration algorithms. Additionally, we have established a data dependence result for the iteration algorithm (8) applied to quasi-strictly contractive mappings. In Sect. 4 we have demonstrated several collage theorems that employ a fractal-based approach to provide alternative insights into data dependence of fixed points of quasi-strictly contractive mappings, as well as to solve inverse problems that arise in relation to this class of mappings.

The following lemma plays a key role in obtaining our results.

Lemma 1

(See Liu 1990) Let $\left\{ \Phi _{n}^{i}\right\} _{n=0}^{\infty },i=1,2$ be two sequences such that $\Phi _{k}^{1},\Phi _{k}^{2}\ge 0$, $\forall k\in \mathbb {N}$, $\lim _{k\rightarrow \infty }\Phi _{k}^{2}=0$, and

$$\begin{aligned} \Phi _{k+1}^{1}\le \wp \Phi _{k}^{1}+\Phi _{k}^{2},\forall k\in \mathbb {N} , \end{aligned}$$

in which $\wp \in \left[ 0,1\right)$ is a constant. It then holds that $\lim _{k\rightarrow \infty }\Phi _{k}^{1}=0$.

In the subsequent sections, unless otherwise stated, $\mathbb {T}:\mathbb { S\rightarrow S}$ stands for the quasi-strictly contractive mapping with a fixed point $r^{*}$ in (iii) of Definition 1, $\left\{ t_{k}^{1}\right\} _{k=0}^{\infty }$ and $\left\{ \widetilde{t} _{k}^{1}\right\} _{k=0}^{\infty }$denote the sequences generated by TTP iteration algorithm in (8) with real sequences $\left\{ \upsilon _{k}^{i}\right\} _{n=0}^{\infty }\subseteq \left[ 0,1\right] ,i=1,2,3$ associated to $\mathbb {T}$ and $\widetilde{\mathbb {T}}:\mathbb {S\rightarrow S }$, respectively.

2 Convergence analysis for TTP and S iteration algorithms

In this section, results regarding the convergence and equivalence of convergence of the TTP and S iteration algorithms of quasi-contractive mappings will be presented.

Theorem 2

The sequence $\left\{ t_{k}^{1}\right\} _{n=0}^{\infty }$ strongly converges to $r^{*}$ with the following estimate:

$$\begin{aligned} \left\| t_{k+1}^{1}-r^{*}\right\| \le K^{k+1}\prod \limits _{n=0}^{k}\left[ 1-\upsilon _{n}^{1}\upsilon _{n}^{2}\left( 1-K\right) \right] \left[ 1-\upsilon _{n}^{3}(1-K)\right] \left\| t_{0}^{1}-r^{*}\right\| \text {, }\forall k\in \mathbb {N} \text {.} \end{aligned}$$

(10)

Proof

It follows from (iii) of Definition 1 and (8) that

$$\begin{aligned} \left\| t_{k+1}^{1}-r^{*}\right\|\le & {} (1-\upsilon _{k}^{1})\left\| \mathbb {T}t_{k}^{3}-r^{*}\right\| +\upsilon _{k}^{1}\left\| \mathbb {T}t_{k}^{2}-r^{*}\right\| \\\le & {} (1-\upsilon _{k}^{1})K\left\| t_{k}^{3}-r^{*}\right\| +\upsilon _{k}^{1}K\left\| t_{k}^{2}-r^{*}\right\| \\\le & {} (1-\upsilon _{k}^{1})K\left\{ (1-\upsilon _{k}^{3})\left\| t_{k}^{1}-r^{*}\right\| +\upsilon _{k}^{3}\left\| \mathbb {T} t_{k}^{1}-r^{*}\right\| \right\} \\{} & {} +\upsilon _{k}^{1}K\left\{ (1-\upsilon _{k}^{2})\left\| t_{k}^{3}-r^{*}\right\| +\upsilon _{k}^{2}\left\| \mathbb {T} t_{k}^{3}-r^{*}\right\| \right\} \\\le & {} (1-\upsilon _{k}^{1})K\left[ (1-\upsilon _{k}^{3}\left( 1-K\right) \right] \left\| t_{k}^{1}-r^{*}\right\| \\{} & {} +\upsilon _{k}^{1}K\left[ (1-\upsilon _{k}^{2}\left( 1-K\right) \right] \left\| t_{k}^{3}-r^{*}\right\| \\\le & {} K\left[ 1-\upsilon _{k}^{1}\upsilon _{k}^{2}\left( 1-K\right) \right] \left[ 1-\upsilon _{k}^{3}(1-K)\right] \left\| t_{k}^{1}-r^{*}\right\| \text {, }\forall k\in \mathbb {N} \text {,} \end{aligned}$$

which implies that

$$\begin{aligned} \left\| t_{k+1}^{1}-r^{*}\right\| \le K^{k+1}\pi _{k}\left\| t_{0}^{1}-r^{*}\right\| \text {, }\forall k\in \mathbb {N} \text {,} \end{aligned}$$

(11)

in which $\pi _{k}=\prod \nolimits _{n=0}^{k}\left[ 1-\upsilon _{n}^{1}\upsilon _{n}^{2}\left( 1-K\right) \right] \left[ 1-\upsilon _{n}^{3}(1-K)\right]$. Since $0\le \upsilon _{k}^{1},\upsilon _{k}^{2},\upsilon _{k}^{3}\le 1$ for all $k\in \mathbb {N}$ and $K\in \left[ 0,1\right)$, $\pi _{k}\in \left[ 0,1\right]$ for all $k\in \mathbb {N}$ and $\lim _{k\rightarrow \infty }K^{k+1}=0$. Hence, $\left\{ \pi _{k}\right\} _{k=0}^{\infty }$ is a bounded sequence of non-negative real numbers and $\lim _{k\rightarrow \infty }K^{k+1}\pi _{k}=0$. Keeping in mind the latter and passing to the limit in (11), we get $\lim _{k\rightarrow \infty }\left\| t_{k}^{1}-r^{*}\right\| =0$. $\square$

Example 2

Let $\mathbb {S}$ be the Banach space $\left( C\left[ 0,1\right] ,\left\| \cdot \right\| \right)$, where $\left\| \cdot \right\|$ is the supremum norm on $C\left[ 0,1\right]$ defined by $\left\| \cdot \right\| =\left\{ \sup \left| r\left( \tau \right) \right| :\tau \in \left[ 0,1\right] \right\}$. Consider the following first order initial value problem (IVP)

$$\begin{aligned} r^{\prime }\left( \tau \right) =e^{\tau -2}r\left( \tau \right) +e^{2\tau },\ \ r\left( 0\right) =1. \end{aligned}$$

(12)

Finding a solution of IVP (12), if any, is equivalent to finding a fixed point of an integral operator $\mathbb {T}:C\left[ 0,1\right] \rightarrow C\left[ 0,1\right]$ defined by

$$\begin{aligned} \mathbb {T}\left( r\left( \tau \right) \right) =r\left( 0\right) +\int _{0}^{\tau }\left[ e^{s-2}r\left( s\right) +e^{2s}\right] ds. \end{aligned}$$

(13)

A routine computation yields that $r^{*}\left( \tau \right) =e^{e^{-2}\left( e^{\tau }-1\right) }\left( e^{2}+e^{4}+1\right) -e^{4}-e^{\tau +2}\in C\left[ 0,1\right]$ is the unique fixed point of $\mathbb {T}$ in (13) and $\mathbb {T}$ is a quasi-strictly contractive mapping with $r^{*}\left( \tau \right)$ and contractivity factor $K=e^{-1}\in \left[ 0,1\right)$. Hence, by Theorem 2, the sequence $\{t_{k}^{1}\left( \tau \right) \}$ generated by iterative algorithm (8) of $\mathbb {T}$ in (13) converges to $r^{*}\left( \tau \right)$ for the initial function $r_{0}\left( \tau \right) =1$ as shown in Table 1 and Fig. 1.

Table 1 $|t_{k}^{1}\left( \tau \right) -r^{*}\left( \tau \right) |$ for $k=1,3,6$

Fig. 1

Graphs of $t_{k}^{1}\left( \tau \right)$ for $k=1,3,6$

Theorem 3

The iterative sequence $\left\{ s_{k}^{1}\right\} _{n=0}^{\infty }$ in (7) strongly converges to $r^{*}$ with the following estimate:

$$\begin{aligned} \left\| s_{k+1}^{1}-r^{*}\right\| \le K^{k+1}\prod \limits _{n=0}^{k}\left[ 1-\upsilon _{n}^{1}\upsilon _{n}^{2}\left( 1-K\right) \right] \left\| s_{0}^{1}-r^{*}\right\| \text {, }\forall k\in \mathbb {N} \text {.} \end{aligned}$$

(14)

Proof

Similar to the proof of Theorem 2. $\square$

Example 3

Suppose we have the same $\mathbb {S}$ and $\mathbb {T}$ as in Example 2. Then, by Theorem 3, the sequence $\{s_{k}^{1}\left( \tau \right) \}$ generated by the iterative algorithm (7) of $\mathbb {T}$ in (13) converges to $r^{*}\left( \tau \right)$ for the initial function $r_{0}\left( \tau \right) =1$ as shown in Table 2 and Fig. 2.

Table 2 $|s_{k}^{1}\left( \tau \right) -r^{*}\left( \tau \right) |$ for $k=1,3,6$

Fig. 2

Graphs of $s_{k}^{1}\left( \tau \right)$ for $k=1,3,6$

Theorem 4

The following statements are hold:

• (i) The sequence $\left\{ t_{k}^{1}-s_{k}^{1}\right\} _{n=0}^{\infty }$ strongly converges to 0 with the following estimate

  $$\begin{aligned} \left\| t_{k+1}^{1}-s_{k+1}^{1}\right\| \le K\left\| t_{k}^{1}-s_{k}^{1}\right\| +2K\left\| t_{k}^{1}-r^{*}\right\| , \text { }\forall k\in \mathbb {N} \text {,} \end{aligned}$$

  (15)

  and $\left\{ s_{k}^{1}\right\} _{n=0}^{\infty }$ strongly converges to $r^{*}$.

• (ii) The sequence $\left\{ s_{k}^{1}-t_{k}^{1}\right\} _{n=0}^{\infty }$ strongly converges to 0 with the following estimate

$$\begin{aligned} \left\| s_{k+1}^{1}-t_{k+1}^{1}\right\| \le K\left\| s_{k}^{1}-t_{k}^{1}\right\| +2K\left\| s_{k}^{1}-r^{*}\right\| , \text { }\forall k\in \mathbb {N} \text {,} \end{aligned}$$

(16)

and $\left\{ t_{k}^{1}\right\} _{n=0}^{\infty }$ strongly converges to $r^{*}$.

Proof

Since $0\le \upsilon _{k}^{1},\upsilon _{k}^{2},\upsilon _{k}^{3}\le 1$, $\forall k\in \mathbb {N}$ and $K\in \left[ 0,1\right)$,

$$\begin{aligned} 1-\upsilon _{k}^{i}\left( 1-K\right)<1,i=1,2,3\text { and }1-\upsilon _{k}^{1}\upsilon _{k}^{2}\left( 1-K\right) <1,\forall k\in \mathbb {N} . \end{aligned}$$

(17)

• (i) It follows from (iii) of Definition 1, (8), (7), and (17) that

  $$\begin{aligned} \left\| t_{k+1}^{1}-s_{k+1}^{1}\right\|\le & {} \left\| (1-\upsilon _{k}^{1})(\mathbb {T}t_{k}^{3}-r^{*})+\upsilon _{k}^{1}(\mathbb {T} t_{k}^{2}-r^{*})\right\| \nonumber \\{} & {} +\left\| (1-\upsilon _{k}^{1})(r^{*}-\mathbb {T}s_{k}^{1})-\upsilon _{k}^{1}(r^{*}-\mathbb {T}s_{k}^{2})\right\| \nonumber \\\le & {} (1-\upsilon _{k}^{1})\left\| \mathbb {T}t_{k}^{3}-r^{*}\right\| +\upsilon _{k}^{1}\left\| \mathbb {T}t_{k}^{2}-r^{*}\right\| \nonumber \\{} & {} +(1-\upsilon _{k}^{1})\left\| r^{*}-\mathbb {T}s_{k}^{1}\right\| +\upsilon _{k}^{1}\left\| r^{*}-\mathbb {T}s_{k}^{2}\right\| \nonumber \\\le & {} (1-\upsilon _{k}^{1})K\left\| t_{k}^{3}-r^{*}\right\| +\upsilon _{k}^{1}K\left\| t_{k}^{2}-r^{*}\right\| \nonumber \\{} & {} +(1-\upsilon _{k}^{1})K\left\| r^{*}-s_{k}^{1}\right\| +\upsilon _{k}^{1}K\left\| r^{*}-s_{k}^{2}\right\| \nonumber \\\le & {} K\left[ 1-\upsilon _{k}^{1}\upsilon _{k}^{2}\left( 1-K\right) \right] \left\| r^{*}-s_{k}^{1}\right\| \nonumber \\{} & {} +\upsilon _{k}^{1}K\left[ 1-\upsilon _{k}^{2}\left( 1-K\right) \right] \left[ 1-\upsilon _{k}^{3}\left( 1-K\right) \right] \left\| t_{k}^{1}-r^{*}\right\| \nonumber \\{} & {} +(1-\upsilon _{k}^{1})K\left[ 1-\upsilon _{k}^{3}\left( 1-K\right) \right] \left\| t_{k}^{1}-r^{*}\right\| \nonumber \\= & {} K\left[ 1-\upsilon _{k}^{1}\upsilon _{k}^{2}\left( 1-K\right) \right] \left\| t_{k}^{1}-s_{k}^{1}\right\| \nonumber \\{} & {} +K\left\{ 1+\left[ 1-\upsilon _{k}^{3}\left( 1-K\right) \right] \right\} \left[ 1-\upsilon _{k}^{1}\upsilon _{k}^{2}\left( 1-K\right) \right] \left\| t_{k}^{1}-r^{*}\right\| \nonumber \\\le & {} K\left\| t_{k}^{1}-s_{k}^{1}\right\| +2K\left\| t_{k}^{1}-r^{*}\right\| ,\text { }\forall k\in \mathbb {N} \text {.} \end{aligned}$$

  (18)

  By Theorem 2, we have $\lim _{k\rightarrow \infty }\left\| t_{k}^{1}-r^{*}\right\| =0$ which implies that $\lim _{k\rightarrow \infty }2K\left\| t_{k}^{1}-r^{*}\right\| =0$. Hence, by Lemma 1, we get $\lim _{k\rightarrow \infty }\left\| t_{k}^{1}-s_{k}^{1}\right\| =0$. On the other hand, we have

  $$\begin{aligned} \left\| s_{k}^{1}-r^{*}\right\| \le \left\| s_{k}^{1}-t_{k}^{1}\right\| +\left\| t_{k}^{1}-r^{*}\right\| , \text { }\forall k\in \mathbb {N} \text {.} \end{aligned}$$

  (19)

  Passing to the limit in (19) gives $\lim _{k\rightarrow \infty }\left\| s_{k}^{1}-r^{*}\right\| =0$.

• (ii) The proof is immediate by interchanging the roles of $\left\{ s_{k}^{1}\right\} _{n=0}^{\infty }$ and $\left\{ t_{k}^{1}\right\} _{n=0}^{\infty }$ in the part (i). $\square$

Example 4

Consider $\mathbb {S}$ as the Banach space $C^{(2)}([0,1]\times \mathbb {R})$, the space of all bounded continuous two-times differentiable real valued function on $[0,1]\times \mathbb {R}$ equipped with $\left\| \cdot \right\| =\left\{ \sup \left| r\left( x,\tau \right) \right| :\tau \in \left[ 0,1\right] ,x\in \mathbb {R} \right\}$. We tackle following hyperbolic PDE problem

$$\begin{aligned} r_{xx}+r_{\tau \tau }-4r_{\tau }-2r= & {} 0,\text { }0\le \tau \le 1 \nonumber \\ \text { }r(x,0)= & {} \sin x,\text { }r(x,1)=e^{-1}\sin x \end{aligned}$$

(20)

(see Kafri and Khuri 2016). The exact solution of (20) is $r^{*}(x,\tau )=e^{-\tau }\sin x$. Showing existence of solutions of (20) is equivalent to find a solution to a mapping $\mathbb {T}$ $:S\rightarrow S$ given by

$$\begin{aligned} \mathbb {T}r=r+\int _{0}^{1}\mathbb {G}(s,\tau )(r_{xx}+r_{ss}-4r_{s}-2r)ds \end{aligned}$$

(21)

in which

$$\begin{aligned} \mathbb {G}(s,\tau )=\left\{ \begin{array}{c} s(1-\tau ),\quad 0<\tau<s \\ \tau (1-s),\quad s<\tau <1 \end{array} \right. . \end{aligned}$$

(22)

Using the definition of $\mathbb {G}(s,\tau )$ in (22) and integration by parts, we get

$$\begin{aligned} \int _{0}^{1}\mathbb {G}(s,\tau )\big [r_{ss}^{\left( 1\right) }-r_{ss}^{\left( 2\right) }\big ]ds= & {} \mathbb {G}(s,\tau )\big [r_{s}^{\left( 1\right) }-r_{s}^{\left( 2\right) }\big ]_{0}^{1}-\int _{0}^{1}\mathbb {G}_{s}(s,\tau )\big [r_{s}^{\left( 1\right) }-r_{s}^{\left( 2\right) }\big ]ds \\= & {} \mathbb {G}(s,\tau )\big [r_{s}^{\left( 1\right) }-r_{s}^{\left( 2\right) }\big ]_{0}^{1}-\Big [\mathbb {G}_{s}(s,\tau )\big [r_{s}^{\left( 1\right) }-r_{s}^{\left( 2\right) }\big ]_{0}^{1} \\{} & {} -\int _{0}^{1}\mathbb {G}_{ss}(s,\tau )\big [r_{s}^{\left( 1\right) }-r_{s}^{\left( 2\right) }\big ]ds\Big ] \\= & {} s(1-\tau )\big [r_{s}^{\left( 1\right) }-r_{s}^{\left( 2\right) }\big ]_{0}^{\tau }+\tau (1-s)\big [r_{s}^{\left( 1\right) }-r_{s}^{\left( 2\right) }\big ]_{\tau }^{1} \\{} & {} -(1-\tau )\big [r^{\left( 1\right) }-r^{\left( 2\right) }\big ]_{0}^{\tau }+\tau \big [ r^{\left( 1\right) }-r^{\left( 2\right) }\big ]_{\tau }^{1} \\= & {} -(1-\tau )\big [r^{\left( 1\right) }(x,\tau )-r^{\left( 2\right) }(x,\tau )\big ]-\tau \big [r^{\left( 1\right) }(x,\tau )-r^{\left( 2\right) }(x,\tau )\big ] \\= & {} -\big [r^{\left( 1\right) }(x,\tau )-r^{\left( 2\right) }(x,\tau )\big ]\text {,} \end{aligned}$$

and

$$\begin{aligned} \sup _{\tau \in [0,1]}\left| \int _{0}^{1}\mathbb {G}(s,\tau )ds\right| =\frac{1}{8}. \end{aligned}$$

Hence,

$$\begin{aligned} |\mathbb {T}r^{\left( 1\right) }-\mathbb {T}r^{\left( 2\right) }|= & {} \left| r^{\left( 1\right) }+\int _{0}^{1}\mathbb {G}(s,\tau )\big (r_{xx}^{\left( 1\right) }+r_{ss}^{\left( 1\right) }-4r_{s}^{\left( 1\right) }-2r^{\left( 1\right) }\big )ds\right. \\{} & {} \left. -(r^{\left( 2\right) }+\int _{0}^{1}\mathbb {G}(s,\tau )\big (r_{xx}^{\left( 2\right) }+r_{ss}^{\left( 2\right) }-4r_{s}^{\left( 2\right) }-2r^{\left( 2\right) })ds\big )\right| \\= & {} \left| (r^{\left( 1\right) }-r^{\left( 2\right) })+\int _{0}^{1} \mathbb {G}(x,s)\big [r_{ss}^{\left( 1\right) }-r_{ss}^{\left( 2\right) }\big ]ds\right. \\{} & {} \left. +\int _{0}^{1}\mathbb {G}(s,\tau )\big [r_{xx}^{\left( 1\right) }-4r_{s}^{\left( 1\right) }-2r^{\left( 1\right) }\big ]ds\right| \\= & {} \left| \int _{0}^{1}\mathbb {G}(s,\tau )\big [r_{xx}^{\left( 2\right) }-4r_{s}^{\left( 2\right) }-2r^{\left( 2\right) }\big ]ds\right| \\\le & {} \sup _{[0,1]\times R}\left| \int _{0}^{1}\mathbb {G}(s,\tau )ds\right| \sup _{[0,1]\times R}\left| \frac{\partial (r_{xx}^{\left( 1\right) }-4r_{s}^{\left( 1\right) }-2r^{\left( 1\right) })}{\partial r^{\left( 1\right) }}\right| \sup _{[0,1]\times R}|r^{\left( 1\right) }-r^{\left( 2\right) }| \\\le & {} \frac{1}{8}\sup _{[0,1]\times R}|r^{\left( 1\right) }-r^{\left( 2\right) }|\times 2 \\= & {} \frac{1}{4}\sup _{[0,1]\times R}|r^{\left( 1\right) }-r^{\left( 2\right) }|, \end{aligned}$$

that is, $\mathbb {T}$ is a contraction mapping with contractivity factor $K= \frac{1}{4}<1$ and is thus a quasi-strictly contractive mapping with $r^{*}(x,\tau )=e^{-\tau }\sin x$ and $K=\frac{1}{4}\in \left[ 0,1\right)$. Let $\left\{ t_{k}^{1}\left( x,\tau \right) \right\}$ be the sequence generated by the iterative algorithm (8) of $\mathbb {T}$ in (21) and $\left\{ s_{k}^{1}\left( x,\tau \right) \right\}$ a sequence generated by the iterative algorithm (7) of $\mathbb {T}$ in (21). Take $\upsilon _{k}^{i}=\frac{k}{k+1}$ for all $k\in \mathbb {N}$, $i=1,2,3$ and initial function $r_{0}(x,\tau )=\tau (e^{-1}\sin x-\sin x)+\sin x$ which is a solution of

$$\begin{aligned} r_{\tau \tau }= & {} 0,\text { }0\le \tau \le 1 \nonumber \\ r(x,0)= & {} \sin x,\text { }r(x,1)=e^{-1}\sin x. \end{aligned}$$

(23)

Now, by the conclusion of Theorem 4, we have that

• (i) the sequence $\left\{ t_{k}^{1}-s_{k}^{1}\right\} _{k=0}^{\infty }$ strongly converges to 0 with the estimate in (15) and $\left\{ s_{k}^{1}\right\} _{k=0}^{\infty }$ strongly converges to $r^{*}(x,\tau )=e^{-\tau }\sin x$ as shown in Tables 3, 4, and Fig. 3, and

• (ii) the sequence $\left\{ s_{k}^{1}-t_{k}^{1}\right\} _{k=0}^{\infty }$ strongly converges to 0 with the estimate in (16) and $\left\{ t_{k}^{1}\right\} _{k=0}^{\infty }$ strongly converges to $r^{*}(x,\tau )=e^{-\tau }\sin x$ as shown in Tables 3, 5, and Fig. 4.

Table 3 $|t_{k}^{1}-s_{k}^{1}|$ for $k=10,20,30,40,50$ where ${t_{k}^{1}}$ generated by algor. (8) and ${s_{k}^{1}}$ generated by algor. (7)

Table 4 $|s_{k}^{1}-r^{*}|$ for $k=1,5,9$

Fig. 3

Convergence of $s^{1}_{k}$ towards the solution $r^{*}$ $(x,\tau )$ for selected k values (1, 5, 9) across varying $\tau$ values

In the example below, we compare the convergence performance of iteration algorithms in (8) and (7).

Example 5

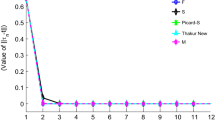
Suppose we have $\mathbb {S}$, $\mathbb {T}$, $\left\{ t_{k}^{1}\left( \tau \right) \right\}$ as described in Example 2 and $\left\{ s_{k}^{1}\left( \tau \right) \right\}$ as described in Example 3. Both sequences, $\left\{ t_{k}^{1}\left( \tau \right) \right\}$ and $\left\{ s_{k}^{1}\left( \tau \right) \right\}$, converge to $r^{*}\left( \tau \right)$ for the initial function $r_{0}\left( \tau \right) =1$ as shown in Examples 2 and 3, respectively. Take $\upsilon _{k}^{i}=\frac{k}{k+1}$ for all $k\in \mathbb {N}$, $i=1,2,3$. Table 6 and Fig. 5 show that $\left\{ t_{k}^{1}\left( \tau \right) \right\}$ converges faster than $\left\{ s_{k}^{1}\left( \tau \right) \right\}$ to $r^{*}\left( \tau \right)$.

Table 5 $|t_{k}^{1}-r^{*}|$ for $k=1,5,9$

Fig. 4

Convergence of $t^{1}_{k}$ towards the solution $r^{*}$ $(x,\tau )$ for selected k values (1, 5, 9) across varying $\tau$ values

Table 6 $|t_{k}^{1}-r^{*}|$ and $|s_{k}^{1}-r^{*}|$ for $k=1,3,6$

Fig. 5

Graphs of $|t_{k}^{1}$ and $|s_{k}^{1}$ for $k=1,3,6$

3 Stability and data dependence results for TTP iteration algorithm

In this section, we will revisit the stability and data dependency results presented in Theorem 1 in order to develop them further.

Theorem 5

Let $\left\{ r_{k}^{1}\right\} _{k=0}^{\infty }\subset \mathbb {S}$ be a sequence and define $\Theta _{k}\in \mathbb {R} ^{+}$as

$$\begin{aligned} \Theta _{k}=\left\| r_{k+1}^{1}-(1-\upsilon _{k}^{1})\mathbb {T} r_{k}^{3}-\upsilon _{k}^{1}\mathbb {T}r_{k}^{2}\right\| \text {, }\forall k\in \mathbb {N} \text {,} \end{aligned}$$

(24)

in which $r_{k}^{2}=(1-\upsilon _{k}^{2})r_{k}^{3}+\upsilon _{k}^{2}\mathbb {T }r_{k}^{3}$ and $r_{k}^{3}=(1-\upsilon _{k}^{3})r_{k}^{1}+\upsilon _{k}^{3} \mathbb {T}r_{k}^{1}$, $\forall k\in \mathbb {N}$. If   $\lim _{k\longrightarrow \infty }\Theta _{k}=0$, then TTP iteration algorithm is stable w.r.t $\mathbb {T}$.

Proof

We shall prove that $\lim _{k\longrightarrow \infty }r_{k}^{1}=r^{*}$. Using (iii) of Definition 1, (5), (8), and (24 ), we get

$$\begin{aligned} \left\| r_{k+1}^{1}-r^{*}\right\|\le & {} \left\| r_{k+1}^{1}-t_{k+1}^{1}\right\| +\left\| t_{k+1}^{1}-r^{*}\right\| \nonumber \\\le & {} \left\| r_{k+1}^{1}-(1-\upsilon _{k}^{1})\mathbb {T} r_{k}^{3}-\upsilon _{k}^{1}\mathbb {T}r_{k}^{2}\right\| \nonumber \\{} & {} +(1-\upsilon _{k}^{1})\left\| \mathbb {T}r_{k}^{3}-\mathbb {T} t_{k}^{3}\right\| +\upsilon _{k}^{1}\left\| \mathbb {T}r_{k}^{2}- \mathbb {T}t_{k}^{2}\right\| +\left\| t_{k+1}^{1}-r^{*}\right\| \nonumber \\\le & {} \Theta _{k}+(1-\upsilon _{k}^{1})\left\{ K\left\| r_{k}^{3}-t_{k}^{3}\right\| +2K\left\| t_{k}^{3}-r^{*}\right\| \right\} \nonumber \\{} & {} +\upsilon _{k}^{1}\left\{ K\left\| r_{k}^{2}-t_{k}^{2}\right\| +2K\left\| t_{k}^{2}-r^{*}\right\| \right\} +\left\| t_{k+1}^{1}-r^{*}\right\| \nonumber \\\le & {} \Theta _{k}+(1-\upsilon _{k}^{1})K\left\| (1-\upsilon _{k}^{3})(r_{k}^{1}-t_{k}^{1})+\upsilon _{k}^{3}(\mathbb {T}r_{k}^{1}-\mathbb { T}t_{k}^{1})\right\| \nonumber \\{} & {} +(1-\upsilon _{k}^{1})2K\left\| (1-\upsilon _{k}^{3})(t_{k}^{1}-r^{*})+\upsilon _{k}^{3}(\mathbb {T}t_{k}^{1}-r^{*})\right\| \nonumber \\{} & {} +\upsilon _{k}^{1}K\left\| (1-\upsilon _{k}^{2})(r_{k}^{3}-t_{k}^{3})+\upsilon _{k}^{2}(\mathbb {T}r_{k}^{3}-\mathbb { T}t_{k}^{3})\right\| \nonumber \\{} & {} +\upsilon _{k}^{1}2K\left\| (1-\upsilon _{k}^{2})(t_{k}^{3}-r^{*})+\upsilon _{k}^{2}(\mathbb {T}t_{k}^{3}-r^{*})\right\| +\left\| t_{k+1}^{1}-r^{*}\right\| \nonumber \\\le & {} \Theta _{k}+(1-\upsilon _{k}^{1})K\left[ 1-\upsilon _{k}^{3}(1-K) \right] \left\| r_{k}^{1}-t_{k}^{1}\right\| \nonumber \\{} & {} +(1-\upsilon _{k}^{1})\left\{ 2K^{2}\upsilon _{k}^{3}+2K\left[ 1-\upsilon _{k}^{3}(1-K)\right] \right\} \left\| t_{k}^{1}-r^{*}\right\| \nonumber \\{} & {} +\upsilon _{k}^{1}\left\{ 2K^{2}\upsilon _{k}^{2}+2K\left[ 1-\upsilon _{k}^{2}(1-K)\right] \right\} \left\| t_{k}^{3}-r^{*}\right\| \nonumber \\{} & {} +\upsilon _{k}^{1}K\left[ 1-\upsilon _{k}^{2}(1-K)\right] \left\| r_{k}^{3}-t_{k}^{3}\right\| +\left\| t_{k+1}^{1}-r^{*}\right\| \text {, }\forall k\in \mathbb {N} \text {.} \end{aligned}$$

(25)

Applying inequalities in (17) to (25), we attain

$$\begin{aligned} \left\| r_{k+1}^{1}-r^{*}\right\| \le K\left\| r_{k}^{1}-r_{k}^{1}\right\| +\Theta _{k}+M_{k}\left\| t_{k}^{1}-r^{*}\right\| +\left\| t_{k+1}^{1}-r^{*}\right\| \text {, }\forall k\in \mathbb {N} \text {,} \end{aligned}$$

(26)

in which $M_{k}=6+4K\upsilon _{k}^{3}+2K\upsilon _{k}^{2}$, $\forall k\in \mathbb {N}$, is a bounded sequence of non-negative real numbers. Now, we set $\Phi _{k}^{1}:=\left\| r_{k}^{1}-r^{*}\right\| \ge 0$, $\wp :=K\in [0,1)$, and $\Phi _{k}^{2}:=\Theta _{k}+M_{k}\left\| t_{k}^{1}-r^{*}\right\| +\left\| t_{k+1}^{1}-r^{*}\right\| \ge 0$, $\forall k\in \mathbb {N}$. From the facts that $M_{k}$ is a bounded sequence and $\lim _{k\rightarrow \infty }\left\| t_{k}^{1}-r^{*}\right\| =0$ by Theorem 2, we obtain that $\lim _{k\rightarrow \infty }M_{k}\left\| t_{k}^{1}-r^{*}\right\| =0$. Hence, $\lim _{k\rightarrow \infty }\Phi _{k}^{2}=0$ as $\lim _{k\rightarrow \infty }\Theta _{k}=0$. Thus, an application of Lemma 1 to (26) yields $\lim _{k\rightarrow \infty }r_{k}^{1}=r^{*}$.

We must now prove that $\lim _{k\longrightarrow \infty }\Theta _{k}=0$, assuming $\lim _{k\longrightarrow \infty }r_{k}^{1}=r^{*}$. Using (iii) of Definition 1, (5), (8), and (24), we obtain

$$\begin{aligned} \Theta _{k}= & {} \left\| r_{k+1}^{1}-(1-\upsilon _{k}^{1})\mathbb {T} r_{k}^{3}-\upsilon _{k}^{1}\mathbb {T}r_{k}^{2}\right\| \\\le & {} \left\| r_{k+1}^{1}-t_{k+1}^{1}\right\| +\left\| t_{k+1}^{1}-(1-\upsilon _{k}^{1})\mathbb {T}r_{k}^{3}-\upsilon _{k}^{1} \mathbb {T}r_{k}^{2}\right\| \\\le & {} \left\| r_{k+1}^{1}-t_{k+1}^{1}\right\| +(1-\upsilon _{k}^{1})\left\| \mathbb {T}t_{k}^{3}-\mathbb {T}r_{k}^{3}\right\| +\upsilon _{k}^{1}\left\| \mathbb {T}t_{k}^{2}-\mathbb {T} r_{k}^{2}\right\| \\\le & {} \left\| r_{k+1}^{1}-t_{k+1}^{1}\right\| +(1-\upsilon _{k}^{1})\left\{ K\left\| t_{k}^{3}-r_{k}^{3}\right\| +2K\left\| r_{k}^{3}-r^{*}\right\| \right\} \\{} & {} +\upsilon _{k}^{1}\left\{ K\left\| t_{k}^{2}-r_{k}^{2}\right\| +2K\left\| r_{k}^{2}-r^{*}\right\| \right\} \\\le & {} \left\| r_{k+1}^{1}-t_{k+1}^{1}\right\| +K\left[ 1-\upsilon _{k}^{3}(1-K)\right] \left[ 1-\upsilon _{k}^{1}\upsilon _{k}^{2}(1-K)\right] \left\| t_{k}^{1}-r_{k}^{1}\right\| \\{} & {} +2(1-\upsilon _{k}^{1})K\left[ 1-\upsilon _{k}^{3}+2\upsilon _{k}^{3}K \right] \left\| r_{k}^{1}-r^{*}\right\| \\{} & {} +2\upsilon _{k}^{1}\upsilon _{k}^{3}K^{2}\left[ 1-\upsilon _{k}^{2}(1-K) \right] \left\| r_{k}^{1}-r^{*}\right\| \\{} & {} +2\upsilon _{k}^{1}K\left[ 1-\upsilon _{k}^{2}+2\upsilon _{k}^{2}K)\right] \left[ 1-\upsilon _{k}^{3}(1-K)\right] \left\| r_{k}^{1}-r^{*}\right\| ,\forall k\in \mathbb {N} \text {.} \end{aligned}$$

or equivalently

$$\begin{aligned} \Theta _{k}\le \left\| r_{k+1}^{1}-r^{*}\right\| +\left\| t_{k+1}^{1}-r^{*}\right\| +M_{k}^{1}\left\| t_{k}^{1}-r^{*}\right\| +(M_{k}^{1}+M_{k}^{2})\left\| r_{k}^{1}-r^{*}\right\| ,\forall k\in \mathbb {N} \text {,} \end{aligned}$$

(27)

in which

$$\begin{aligned} M_{k}^{1}=K\left[ 1-\upsilon _{k}^{3}(1-K)\right] \left[ 1-\upsilon _{k}^{1}\upsilon _{k}^{2}(1-K)\right] ,\forall k\in \mathbb {N} . \end{aligned}$$

and

$$\begin{aligned} M_{k}^{2}= & {} 2(1-\upsilon _{k}^{1})K\left[ 1-\upsilon _{k}^{3}+2\upsilon _{k}^{3}K\right] \\{} & {} +2\upsilon _{k}^{1}\upsilon _{k}^{3}K^{2}\left[ 1-\upsilon _{k}^{2}(1-K) \right] \\{} & {} +2\upsilon _{k}^{1}K\left[ 1-\upsilon _{k}^{2}+2\upsilon _{k}^{2}K)\right] \left[ 1-\upsilon _{k}^{3}(1-K)\right] ,\forall k\in \mathbb {N}. \end{aligned}$$

Since, by the definition of $\upsilon _{k}^{i},i=1,2,3,\forall$ $k\in \mathbb {N}$ and K, $\left\{ M_{k}^{1}\right\} _{k=0}^{\infty }$ and $\left\{ M_{k}^{2}\right\} _{k=0}^{\infty }$ are bounded sequences of non-negative real numbers, so is $\left\{ M_{k}^{1}+M_{k}^{2}\right\} _{k=0}^{\infty }$. Also, since $\lim _{k\longrightarrow \infty }r_{k}^{1}=r^{*}$ by the assumption and $\lim _{k\rightarrow \infty }\left\| t_{k}^{1}-r^{*}\right\| =0$ by Theorem 2, we obtain that $\lim _{k\rightarrow \infty }(M_{k}^{1}+M_{k}^{2})\left\| r_{k}^{1}-r^{*}\right\| =$ $\lim _{k\rightarrow \infty }M_{k}^{1}\left\| t_{k}^{1}-r^{*}\right\| =0$, and passing to the limit in (27), we find $\lim _{k\longrightarrow \infty }\Theta _{k}=0$, hence the proof. $\square$

Example 6

Let $\mathbb {S}=\left[ 0,1\right]$ be endowed with the usual metric. Define a mapping $\mathbb {T}:\mathbb {S\rightarrow S}$ by

$$\begin{aligned} \mathbb {T}r=\left( r-1\right) \sin ^{2}r+\frac{e^{r}}{\sqrt{r}+2}. \end{aligned}$$

(28)

The MATLAB$^{TM}$ software package calculates that $r^{*}=0.49212...$ is the unique fixed point of $\ \mathbb {T}$ in $\mathbb {S}$. When $r_{1}=0.9,r_{2}=0.8$, we observe that $\left| \mathbb { T}r_{1}-\mathbb {T}r_{2}\right| =0.1068>0.1=\left| r_{1}-r_{2}\right|$. This means that $\mathbb {T}$ is not a contraction mapping (see also Fig. 6a). However, Fig. 6b shows graphically that $\mathbb {T}$ is a quasi-strictly contractive mapping with a contractivity factor $K\ge 0.85$.

Fig. 6

The mapping $\mathbb {T}$ in Example 6 is quasi-strictly contractive but not a contraction mapping

Let $\left\{ t_{k}^{1}\right\}$ and $\left\{ s_{k}^{1}\right\}$ be the sequences generated by the iterative algorithms (8) and (7) of $\mathbb {T}$ in (28), respectively. It follows Theorems 2 and 3 that the sequences $\left\{ t_{k}^{1}\right\}$ and $\left\{ s_{k}^{1}\right\}$ converge to $r^{*}$ for the initial values $t_{0}^{1}=s_{0}^{1}=0$ as shown in Table 7 and Fig. 7, respectively.

Table 7 $|s_{k}^{1}-r^{*}|$ and $|t_{k}^{1}-r^{*}|$ for $k=1:18$

Fig. 7

Performance comparison of sequences $\left\{ s^{1}_{k}\right\}$ and $\left\{ t^{1}_{k}\right\}$ in converging to fixed point $r^{*}$ for Example 6

Take $\left\{ r_{k}^{1}\right\} _{k=0}^{\infty }=\left\{ r^{*}\frac{ k^{10}}{k^{10}+1}+\frac{1}{k^{k}+1}\right\} _{k=0}^{\infty }$. Clearly $\lim _{k\rightarrow \infty }r_{k}^{1}=r^{*}=\mathbb {T}\left( r^{*}\right)$. Set

$$\begin{aligned} \Theta _{k}=\left\| r_{k+1}^{1}-(1-\upsilon _{k}^{1})\mathbb {T} r_{k}^{3}-\upsilon _{k}^{1}\mathbb {T}r_{k}^{2}\right\| \text {, }\forall k\in \mathbb {N}\text {,} \end{aligned}$$

(29)

in which $r_{k}^{2}=(1-\upsilon _{k}^{2})r_{k}^{3}+\upsilon _{k}^{2}\mathbb {T }r_{k}^{3}$ and $r_{k}^{3}=(1-\upsilon _{k}^{3})r_{k}^{1}+\upsilon _{k}^{3} \mathbb {T}r_{k}^{1}$, $\forall k\in \mathbb {N}$. Table 8 shows that $\lim _{k\longrightarrow \infty }\Theta _{k}=0$. Now all the requirements of Theorem 5 are satisfied and hence, by its conclusion, the iterative algorithm (8) is stable w.r.t. $\mathbb {T}$.

Sometimes it can be challenging, or even impossible, to locate a fixed point of an operator. When faced with such circumstances, rather than calculating the fixed point of that operator, we can utilize a different operator whose fixed points are readily available to estimate the fixed point of the original operator. This technique, which can be considered as a kind of stability, is known as "Data Dependency" in the field. Recently, this topic has gained significant attention due to its potential for exciting and promising applications.

Theorem 6

Let $\mathbb {T}$, $\widetilde{\mathbb {T}}:\mathbb {S\rightarrow S}$ be two mappings with unique fixed points $r^{*}$and $\widetilde{r}^{*}$, respectively. If

(C1) $\mathbb {T}$ is a contraction with contractivity factor $K\in \left[ 0,1\right)$,

(C2) there exists a maximum admissible error $\epsilon >0$ such that $\left\| \mathbb {T}r\mathbb {-}\widetilde{\mathbb {T}}r\right\| \le \epsilon$, $\forall r\in \mathbb {S}$,     and

(C3) $\lim _{k\rightarrow \infty }\widetilde{t}_{k}^{1}=\widetilde{r}^{*}$ ,

then it holds that

$$\begin{aligned} \left\| r^{*}-\widetilde{r}^{*}\right\| \le \left( \frac{1+3K }{1-K}\right) \epsilon \text {.} \end{aligned}$$

(30)

Table 8 Values of $\Theta _{k}$ for $k=1,3,3,10,20,30,35,40$

Proof

Let $\left\{ t_{k}^{1}\right\} _{k=0}^{\infty }$ be the sequences generated by TTP iteration algorithm (8) associated with $\mathbb {T}$ in (C1) with real sequences $\left\{ \upsilon _{k}^{i}\right\} _{n=0}^{\infty }\subseteq \left[ 0,1\right] ,i=1,2,3$. As in the proof of Theorem 2, it can be easily shown that $\lim _{k\rightarrow \infty }t_{k}^{1}=r^{*}$ . Following the steps similar to the proof of (Usurelu et al. 2021, Theorem 4.8), we obtain

$$\begin{aligned} \left\| t_{k+1}^{1}-\widetilde{t}_{k+1}^{1}\right\|\le & {} K\left[ 1-\upsilon _{k}^{1}\upsilon _{k}^{2}\left( 1-K\right) \right] \left[ 1-\upsilon _{k}^{3}\left( 1-K\right) \right] \left\| t_{k}^{1}-\widetilde{ t}_{k}^{1}\right\| \\{} & {} +K(1-\upsilon _{k}^{1})\upsilon _{k}^{3}\epsilon +K\left[ 1-\upsilon _{k}^{2}\left( 1-K\right) \right] \upsilon _{k}^{1}\upsilon _{k}^{3}\epsilon \\{} & {} +K\upsilon _{k}^{1}\upsilon _{k}^{2}\epsilon +(1-\upsilon _{k}^{1})\epsilon +\upsilon _{k}^{1}\epsilon \end{aligned}$$

which implies

$$\begin{aligned} \left\| t_{k+1}^{1}-\widetilde{t}_{k+1}^{1}\right\| \le K\left\| t_{k}^{1}-\widetilde{t}_{k}^{1}\right\| +\left( 1+3K\right) \epsilon ,\forall k\in \mathbb {N}. \end{aligned}$$

(31)

Keeping in mind the fact $\lim _{k\rightarrow \infty }t_{k}^{1}=r^{*}$ and assumption (C3), passing to the limit in (31), we get

$$\begin{aligned} \left\| r^{*}-\widetilde{r}^{*}\right\| \le K\left\| r^{*}-\widetilde{r}^{*}\right\| +\left( 1+3K\right) \epsilon , \end{aligned}$$

or equivalently

$$\begin{aligned} \left\| r^{*}-\widetilde{r}^{*}\right\| \le \left( \frac{1+3K }{1-K}\right) \epsilon . \end{aligned}$$

$\square$

Example 7

Let $\mathbb {S}$, $\mathbb {T}$ be as in Example 4. Let us consider the following hyperbolic PDE problem

$$\begin{aligned} \widetilde{r}_{xx}+\widetilde{r}_{\tau \tau }-4\widetilde{r}_{\tau }-2 \widetilde{r}+x \tau h= & {} 0,\text { }0\le \tau \le 1 \end{aligned}$$

(32)

$$\begin{aligned} \text { }u\left( x,0\right)= & {} \sin x,\text { }u\left( x,1\right) =e^{-1}\sin x. \end{aligned}$$

(33)

The exact solution of (32) is $\widetilde{r}_{*}\left( x,\tau \right)$ which is calculated with MATLAB numerically. $\widetilde{ r}_{*}\left( x,\tau \right)$ is also unique fixed point of $\widetilde{ \mathbb {T}}$ $:S\rightarrow S$ defined by

$$\begin{aligned} \widetilde{\mathbb {T}}\widetilde{r}=\widetilde{r}+\int _{0}^{1}\mathbb {G} \left( s,\tau \right) \left( \widetilde{r}_{xx}+\widetilde{r}_{ss}-4 \widetilde{r}_{s}-2\widetilde{r}+x s h\right) ds \end{aligned}$$

(34)

in which

$$\begin{aligned} \mathbb {G}(s,\tau )=\left\{ \begin{array}{c} s(1-\tau ),\quad 0<\tau<s \\ \tau (1-s),\quad s<\tau <1 \end{array}\right. \end{aligned}$$

(35)

For $\left\{ \widetilde{\upsilon }_{k}^{i}\right\} =\left\{ \frac{k}{k+1} \right\}$, $i=1,2,3$, $h=10^{-10}$, and initial function $\widetilde{t} _{0}^{1}\left( x,\tau \right) =\tau \left( e^{-1}\sin x-\sin x\right) +\sin x$, the sequence $\left\{ \widetilde{t}_{k}^{1}\left( x,\tau \right) \right\}$ generated by the iterative algorithm (8) of $\widetilde{ \mathbb {T}}$ is convergent to $\widetilde{r}_{*}\left( x,\tau \right)$ as shown in Fig. 8.

Fig. 8

Convergence of the sequence $\left\{ \tilde{t}^{1}_{k}(x, \tau )\right\}$ associated with $\mathbb {\tilde{T}}$ in Example 7 to $\tilde{r}_{*} (x, \tau )$ for specified k values (1, 5, 9) across different $\tau$ values

Observe that

$$\begin{aligned} \left\| \mathbb {T}r\mathbb {-}\widetilde{\mathbb {T}}r\right\| \le \epsilon =4.16639(-12),\forall r\in \mathbb {S}. \end{aligned}$$

Therefore, we have

$$\begin{aligned} \left\| r-\widetilde{r}^{*}\right\|&=3.51909(-12) \\&\quad <9.72157(-12) \\&=\left( \frac{1+3\times 0.25}{1-0.25}\right) 4.16639(-12) \\&=\left( \frac{1+3K}{1-K}\right) \epsilon \end{aligned}$$

(see; Fig. 9).

Fig. 9

Verification of the inequality in Eq. (30) for Example 7

Theorem 7

Let $\widetilde{\mathbb {T}}:\mathbb {S\rightarrow S}$ be a mapping with a unique fixed point $\widetilde{r}^{*}$. If

(C1) there exists a maximum admissible error $\epsilon >0$ such that $\left\| \mathbb {T}r\mathbb {-}\widetilde{\mathbb {T}}r\right\| \le \epsilon$, $\forall r\in \mathbb {S}$     and

(C2) $\lim _{k\rightarrow \infty }\widetilde{t}_{k}^{1}=\widetilde{r}^{*}$ ,

then it holds that

$$\begin{aligned} \left\| r^{*}-\widetilde{r}^{*}\right\| \le \left( \frac{2+K}{ 1-K}\right) \epsilon \text {.} \end{aligned}$$

(36)

Proof

By the definitions of $\mathbb {T}$ (a strictly-quasi contractive mapping), $\left\{ {t_{k}^{1}}\right\} _{k=0}^{\infty }$, and $\left\{ \widetilde{t} _{k}^{1}\right\} _{k=0}^{\infty }$, we have

$$\begin{aligned} \left\| t_{k}^{3}-\widetilde{t}_{k}^{3}\right\|= & {} \left\| (1-\upsilon _{k}^{3})t_{k}^{1}+\upsilon _{k}^{3}\mathbb {T} t_{k}^{1}-(1-\upsilon _{k}^{3})\widetilde{t}_{k}^{1}-\upsilon _{k}^{3} \widetilde{\mathbb {T}}\widetilde{t}_{k}^{1}\right\| \nonumber \\\le & {} (1-\upsilon _{k}^{3})\left\| t_{k}^{1}-\widetilde{t} _{k}^{1}\right\| +\upsilon _{k}^{3}\left\| \mathbb {T}t_{k}^{1}- \widetilde{\mathbb {T}}\widetilde{t}_{k}^{1}\right\| \nonumber \\\le & {} \left[ 1-\upsilon _{k}^{3}\left( 1-K\right) \right] \left\| t_{k}^{1}-\widetilde{t}_{k}^{1}\right\| +2K\upsilon _{k}^{3}\left\| t_{k}^{1}-r^{*}\right\| +\upsilon _{k}^{3}\left\| \mathbb {T} \widetilde{t}_{k}^{1}-\widetilde{\mathbb {T}}\widetilde{t}_{k}^{1}\right\| , \nonumber \\ \end{aligned}$$

(37)

$$\begin{aligned} \left\| t_{k}^{2}-\widetilde{t}_{k}^{2}\right\|= & {} \left\| (1-\upsilon _{k}^{2})t_{k}^{3}+\upsilon _{k}^{2}\mathbb {T} t_{k}^{3}-(1-\upsilon _{k}^{2})\widetilde{t}_{k}^{3}-\upsilon _{k}^{2} \widetilde{\mathbb {T}}\widetilde{t}_{k}^{3}\right\| \nonumber \\\le & {} (1-\upsilon _{k}^{2})\left\| t_{k}^{3}-\widetilde{t} _{k}^{3}\right\| +\upsilon _{k}^{2}\left\| \mathbb {T}t_{k}^{3}- \widetilde{\mathbb {T}}\widetilde{t}_{k}^{3}\right\| \nonumber \\\le & {} \left[ 1-\upsilon _{k}^{2}\left( 1-K\right) \right] \left\| t_{k}^{3}-\widetilde{t}_{k}^{3}\right\| +2K\upsilon _{k}^{2}\left\| t_{k}^{3}-r^{*}\right\| +\upsilon _{k}^{2}\left\| \mathbb {T} \widetilde{t}_{k}^{3}-\widetilde{\mathbb {T}}\widetilde{t}_{k}^{3}\right\| , \nonumber \\ \end{aligned}$$

(38)

$$\begin{aligned} \left\| t_{k}^{3}-r^{*}\right\|\le & {} \left[ 1-\upsilon _{k}^{3}\left( 1-K\right) \right] \left\| t_{k}^{1}-r^{*}\right\| , \end{aligned}$$

(39)

$$\begin{aligned} \left\| t_{k+1}^{1}-\widetilde{t}_{k+1}^{1}\right\|= & {} \left\| (1-\upsilon _{k}^{1})\mathbb {T}t_{k}^{3}+\upsilon _{k}^{1}\mathbb {T} t_{k}^{2}-(1-\upsilon _{k}^{1})\widetilde{\mathbb {T}}\widetilde{t} _{k}^{3}-\upsilon _{k}^{1}\widetilde{\mathbb {T}}\widetilde{t} _{k}^{2}\right\| \nonumber \\\le & {} (1-\upsilon _{k}^{1})K\left\| t_{k}^{3}-\widetilde{t} _{k}^{3}\right\| +(1-\upsilon _{k}^{1})2K\left\| t_{k}^{3}-r^{*}\right\| +(1-\upsilon _{k}^{1})\left\| \mathbb {T}\widetilde{t} _{k}^{3}-\widetilde{\mathbb {T}}\widetilde{t}_{k}^{3}\right\| \nonumber \\{} & {} +\upsilon _{k}^{1}K\left\| t_{k}^{2}-\widetilde{t}_{k}^{2}\right\| +\upsilon _{k}^{1}2K\left\| t_{k}^{2}-r^{*}\right\| +\upsilon _{k}^{1}\left\| \mathbb {T}\widetilde{t}_{k}^{2}-\widetilde{\mathbb {T}} \widetilde{t}_{k}^{2}\right\| , \end{aligned}$$

(40)

and

$$\begin{aligned} \left\| t_{k}^{2}-r^{*}\right\| \le \left[ 1-\upsilon _{k}^{2}\left( 1-K\right) \right] \left\| t_{k}^{3}-r^{*}\right\| ,\forall k\in \mathbb {N}. \end{aligned}$$

(41)

Combining (37)-(41), we get

$$\begin{aligned} \left\| t_{k+1}^{1}-\widetilde{t}_{k+1}^{1}\right\|\le & {} K\left[ 1-\upsilon _{k}^{1}\upsilon _{k}^{2}\left( 1-K\right) \right] \left[ 1-\upsilon _{k}^{3}\left( 1-K\right) \right] \left\| t_{k}^{1}-\widetilde{ t}_{k}^{1}\right\| \nonumber \\{} & {} +2(1-\upsilon _{k}^{1})\left\{ \upsilon _{k}^{3}K+1-\upsilon _{k}^{3}\left( 1-K\right) \right\} K\left\| t_{k}^{1}-r^{*}\right\| \nonumber \\{} & {} +2\left\{ \left[ 1-\upsilon _{k}^{2}\left( 1-K\right) \right] \upsilon _{k}^{3}+\left[ 1-\upsilon _{k}^{3}\left( 1-K\right) \right] \upsilon _{k}^{2}\right\} \upsilon _{k}^{1}K^{2}\left\| t_{k}^{1}-r^{*}\right\| \nonumber \\{} & {} +2\left[ 1-\upsilon _{k}^{2}\left( 1-K\right) \right] \left[ 1-\upsilon _{k}^{3}\left( 1-K\right) \right] \upsilon _{k}^{1}K\left\| t_{k}^{1}-r^{*}\right\| \nonumber \\{} & {} +\left[ \left( 1-\upsilon _{k}^{2}\left( 1-K\right) \right) \upsilon _{k}^{3}+\upsilon _{k}^{2}\right] \upsilon _{k}^{1}K\epsilon \nonumber \\{} & {} +(1-\upsilon _{k}^{1})\upsilon _{k}^{3}K\epsilon +(1-\upsilon _{k}^{1})\epsilon +\upsilon _{k}^{1}\epsilon ,\forall k\in \mathbb {N}. \end{aligned}$$

(42)

Exploiting inequalities in (17) and assumption (C1) in (42), we obtain

$$\begin{aligned} \left\| t_{k+1}^{1}-\widetilde{t}_{k+1}^{1}\right\| \le K\left\| t_{k}^{1}-\widetilde{t}_{k}^{1}\right\| +B_{k}\left\| t_{k}^{1}-r^{*}\right\| +\left\{ \upsilon _{k}^{3}K+\upsilon _{k}^{1}+1-\upsilon _{k}^{1}\left( 1-\upsilon _{k}^{2}K\right) \right\} \epsilon ,\forall k\in \mathbb {N}, \end{aligned}$$

(43)

in which

$$\begin{aligned} B_{k}=2(1-\upsilon _{k}^{1})K\left[ 1-\upsilon _{k}^{3}+2\upsilon _{k}^{3}K \right] +2\upsilon _{k}^{1}\upsilon _{k}^{3}K^{2}+\upsilon _{k}^{1}2K\left[ 1-\upsilon _{k}^{2}+2\upsilon _{k}^{2}K\right] . \end{aligned}$$

An application of inequalities $0\le \upsilon _{k}^{1},\upsilon _{k}^{2},\upsilon _{k}^{3}\le 1$, $1-\upsilon _{k}^{1}\left( 1-\upsilon _{k}^{2}K\right) <1$, $\forall k\in \mathbb {N}$, and $K\in \left[ 0,1\right)$ to (43) yields

$$\begin{aligned} \left\| t_{k+1}^{1}-\widetilde{t}_{k+1}^{1}\right\| \le K\left\| t_{k}^{1}-\widetilde{t}_{k}^{1}\right\| +B_{k}\left\| t_{k}^{1}-r^{*}\right\| +\left( 2+K\right) \epsilon ,\forall k\in \mathbb {N}. \end{aligned}$$

(44)

It is clear that $\left\{ B_{k}\right\} _{k=0}^{\infty }$ is a bounded sequences of non-negative real numbers. It is also known from Theorem 2 that $\lim _{k\rightarrow \infty }\left\| t_{k}^{1}-r^{*}\right\|$. Hence, $\lim _{k\rightarrow \infty }B_{k}\left\| t_{k}^{1}-r^{*}\right\| =0$. Keeping in mind this fact and assumption (C2), passing to the limit in (44), we get

$$\begin{aligned} \left\| r^{*}-\widetilde{r}^{*}\right\| \le K\left\| r^{*}-\widetilde{r}^{*}\right\| +\left( 2+K\right) \epsilon , \end{aligned}$$

or equivalently

$$\begin{aligned} \left\| r^{*}-\widetilde{r}^{*}\right\| \le \left( \frac{2+K}{ 1-K}\right) \epsilon . \end{aligned}$$

$\square$

Example 8

Let $\mathbb {S}$, $\mathbb {T}$ be as in Example 6 and let $\widetilde{\mathbb {T}}:\mathbb {S\rightarrow S}$ be defined by

$$\begin{aligned} \widetilde{\mathbb {T}}(r)=(r-1)(-\frac{r^{8}}{315}+\frac{2r^{6}}{45}-\frac{ r^{4}}{3}+r^{2})+\frac{(\frac{r^{8}}{40320}+\frac{r^{7}}{5040}+\frac{r^{6}}{ 720}+\frac{r^{5}}{120}+\frac{r^{4}}{24}+\frac{r^{3}}{24}+\frac{r^{2}}{2}+r+1) }{\sqrt{r}+2} \end{aligned}$$

with unique fixed point $\widetilde{r}^{*}=0.49$ in $\mathbb {S}$. Observe that

$$\begin{aligned} \left( \forall r\in \mathbb {S}\right) \left| \mathbb {T}r \mathbb {-}\widetilde{\mathbb {T}}r\right| \le \epsilon =4.41\times 10^{-6}. \end{aligned}$$

It is also shown in Fig. 10 that the sequence $\left\{ \widetilde{t}_{k}^{1}\right\}$ generated by the iterative algorithm (8) of $\mathbb {T}$ converges to $\widetilde{r}^{*}$ for the initial function $\widetilde{t}_{0}^{1}=1$.

Fig. 10

Graphs of $|t_{k}^{1}-{r}^{*}|$ and $|\widetilde{t}_{k+1}^{1}- \widetilde{r}^{*}|$ for $k=1:20$

Therefore, we have

$$\begin{aligned} \left| r-\widetilde{r}^{*}\right| =7.62\times 10^{-8}<8.369\times 10^{-5}=\left( \frac{2+K}{1-K}\right) \epsilon \ \ \left( K=0.85\right) . \end{aligned}$$

Remark 2

For the upper bound of the error $\left\| r^{*}-\widetilde{r}^{*}\right\|$, the estimate obtained in (30) is much better than the one in (9) as shown below:

$$\begin{aligned} 0< & {} 3K^{2}-2K+6 \\\Rightarrow & {} 0<3K^{2}-3K+K-1+7 \\\Rightarrow & {} \left( 1+3K\right) \left( 1-K\right)<7 \\\Rightarrow & {} \frac{1+3K}{1-K}<\frac{7}{\left( 1-K\right) ^{2}}\text { as } K\in \left[ 0,1\right) \text {.} \end{aligned}$$

Moreover, if it could be allowed putting additional conditions $\lim _{k\rightarrow \infty }\upsilon _{k}^{1}=\lim _{k\rightarrow \infty }\upsilon _{k}^{3}=0$ on $\left\{ \upsilon _{k}^{i}\right\} _{n=0}^{\infty }\subseteq \left[ 0,1\right] ,i=1,3$ in Theorem 6, then one would get a better upper bound for the error $\left\| r^{*}-\widetilde{r}^{*}\right\|$ than the ones in (9) and (30) as under:

$$\begin{aligned} \left\| r^{*}-\widetilde{r}^{*}\right\| \le \frac{\epsilon }{ 1-K}. \end{aligned}$$

The same is true for Theorem 7 as well.

In the next section, we aim to highlight the close relationship between the concepts of data dependency of fixed points and collage theorems. Furthermore, it will be demonstrated that collage theorems actually provide better estimates for the upper bound of the error in approximating $r^{*}$ by $\widetilde{r}^{*}$, i.e. $\left\| r^{*}-\widetilde{r} ^{*}\right\|$.

4 Collage theorems for quasi-strictly contractive mappings

After Mandelbrot’s seminal essay (Mandelbort 1977), fractal-based analysis has emerged as a crucial field of study. Various applications of fractal analysis techniques have proven effective in tackling with both direct and inverse problems in disciplines such as physics, economics, finance, statistics, and image processing (Perna and Sibillo 2008; Yang 2013; Kunze et al. 2011; Barnsley et al. 2011). The Collage theorem (Barnsley et al. 1986), which is a simple outcome of Banach contraction theorem, provides the mathematical foundation for fractal-based approximation. This result plays a significant role in the applications of Banach contraction theorem, particularly in the use of iterated function systems (IFSs) and solving inverse problems for DEs and PDEs (Kunze et al. 2004, 2007; Levere et al. 2013). The objective is to seek a particular mapping $\mathbb {T}$ that minimizes the Collage distance $\left\| r-\mathbb {T}r\right\|$, which allows the approximation error $\left\| r^{*}-r\right\|$ to be as small as possible.

In the following, we extend the Collage theorem to the class of quasi-contractive operators.

Theorem 8

Let $\mathbb {T}$ be quasi-strictly contractive mapping with a fixed point $r^{*}\in \mathbb {S}$. Then, we have

$$\begin{aligned} \frac{1}{1+K}\left\| r-\mathbb {T}r\right\| \le \left\| r^{*}-r\right\| \le \frac{1}{1-K}\left\| r-\mathbb {T}r\right\| \text {, }\forall r\in \mathbb {S}\text {.} \end{aligned}$$

(45)

Proof

If $r^{*}=r$, then (45) is obvious. Suppose that $r^{*}\ne r$ , for any $r\in \mathbb {S}$. Then, by the quasi-strictly contractiveness of $\mathbb {T}$ and triangle inequality for norms, we have

$$\begin{aligned} \left\| r^{*}-r\right\|\le & {} \left\| r^{*}-\mathbb {T} r\right\| +\left\| r-\mathbb {T}r\right\| \\\le & {} K\left\| r^{*}-r\right\| +\left\| r-\mathbb {T} r\right\| \text {,} \end{aligned}$$

or

$$\begin{aligned} \left\| r^{*}-r\right\| \le \frac{1}{1-K}\left\| r-\mathbb {T} r\right\| \text {.} \end{aligned}$$

(46)

Similarly, we get

$$\begin{aligned} \left\| r-\mathbb {T}r\right\|\le & {} \left\| r-r^{*}\right\| +\left\| r^{*}-\mathbb {T}r\right\| \\\le & {} \left\| r-r^{*}\right\| +K\left\| r^{*}-r\right\| \text {,} \end{aligned}$$

or

$$\begin{aligned} \frac{1}{1+K}\left\| r-\mathbb {T}r\right\| \le \left\| r^{*}-r\right\| \text {.} \end{aligned}$$

(47)

Combining (46) and (47), we attain

$$\begin{aligned} \frac{1}{1+K}\left\| r-\mathbb {T}r\right\| \le \left\| r^{*}-r\right\| \le \frac{1}{1-K}\left\| r-\mathbb {T}r\right\| \text {.} \end{aligned}$$

$\square$

Example 9

Let $\mathbb {S}$, $\mathbb {T}$ be as in Example 6. It is shown in Fig. 11 that (45) is satisfied.

Fig. 11

Graphs of $\frac{1}{1+K}|r-\mathbb {T}r|$,$|r^{*}-r|$ and $\frac{ 1}{1-K}|r-\mathbb {T}r|$

Theorem 9

Let $\mathbb {T}$ be quasi-strictly contractive mapping with a fixed point $r^{*}\in \mathbb {S}$ and $\widetilde{\mathbb {T}}$ be a mapping with a fixed point $\widetilde{r}^{*}\in \mathbb {S}$. Then, we have

$$\begin{aligned} \left\| r^{*}-\widetilde{r}^{*}\right\| \le \frac{1}{1-K} \sup _{r\in \mathbb {S}}\left\| \mathbb {T}r-\widetilde{\mathbb {T}} r\right\| \text {.} \end{aligned}$$

(48)

Proof

By quasi-strictly contractiveness of $\mathbb {T}$ and triangle inequality for norms, we have

$$\begin{aligned} \left\| r^{*}-\widetilde{r}^{*}\right\|\le & {} \left\| r^{*}-\mathbb {T}\widetilde{r}^{*}\right\| +\left\| \mathbb {T} \widetilde{r}^{*}-\widetilde{\mathbb {T}}\widetilde{r}^{*}\right\| \\\le & {} K\left\| r^{*}-\widetilde{r}^{*}\right\| +\sup _{r\in \mathbb {S}}\left\| \mathbb {T}r-\widetilde{\mathbb {T}}r\right\| \text {,} \end{aligned}$$

or

$$\begin{aligned} \left\| r^{*}-\widetilde{r}^{*}\right\| \le \frac{1}{1-K} \sup _{r\in \mathbb {S}}\left\| \mathbb {T}r-\widetilde{\mathbb {T}} r\right\| \text {.} \end{aligned}$$

$\square$

Example 10

Let $\mathbb {S}$, $\mathbb {T}$ be as in Example 2. Let us consider the following first order initial value problem (IVP)

$$\begin{aligned} r^{\prime }\left( \tau \right) =e^{\tau -2}r\left( \tau \right) +\frac{2r^{4} }{3}+\frac{4r^{3}}{3}+2r^{2}+2r+1,\ \ r\left( 0\right) =1. \end{aligned}$$

(49)

Finding solution of IVP (49) is equivalent to finding a fixed point of an integral operator $\widetilde{\mathbb {T}}:C\left[ 0,1\right] \rightarrow C\left[ 0,1\right]$ defined by

$$\begin{aligned} \widetilde{\mathbb {T}}\left( r\left( \tau \right) \right) =r\left( 0\right) +\int _{0}^{\tau }\left[ e^{s-2}r(s)+\frac{2s^{4}}{3}+\frac{4s^{3}}{3} +2s^{2}+2s+1\right] ds. \end{aligned}$$

(50)

It can be checked that $\widetilde{r}^{*}\left( \tau \right) =e^{e^{-2}(e^{\tau }-1)}(e^{2}+e^{4}+1)-e^{4}-e^{\tau +2}\in C\left[ 0,1 \right]$ is the unique fixed point of $\widetilde{\mathbb {T}}$. Figure 12 shows that (48) is satisfied for the operators $\mathbb {T}$ and $\widetilde{\mathbb {T}}$.

Fig. 12

$|r^{*}-\widetilde{r}^{*}|$ and $\frac{1}{1-K}\sup |\mathbb { T}r-\widetilde{\mathbb {T}}r|$

Theorem 10

Let $\mathbb {T}$ be quasi-strictly contractive mapping with a fixed point $r^{*}\in \mathbb {S}$ and $\widetilde{\mathbb {T}}$ be a mapping with a fixed point $\widetilde{r}^{*}\in \mathbb {S}$. Assume that

$$\begin{aligned} \sup _{r\in \mathbb {S}}\left\| \mathbb {T}r-\widetilde{\mathbb {T}} r\right\| \le \epsilon \text {,} \end{aligned}$$

(51)

in which $\epsilon >0$ is a constant. Then, we have

$$\begin{aligned} \left\| \widetilde{r}^{*}-\mathbb {T}\widetilde{r}^{*}\right\| \le \left( \frac{1+K}{1-K}\right) \epsilon \text {.} \end{aligned}$$

Proof

By quasi-strictly contractiveness of $\mathbb {T}$ and triangle inequality for norms, we have

$$\begin{aligned} \left\| \widetilde{r}^{*}-\mathbb {T}\widetilde{r}^{*}\right\|\le & {} \left\| \widetilde{r}^{*}-r^{*}\right\| +\left\| r^{*}-\mathbb {T}\widetilde{r}^{*}\right\| \nonumber \\\le & {} \left( 1+K\right) \left\| \widetilde{r}^{*}-r^{*}\right\| . \end{aligned}$$

(52)

Inserting (48) into (52), we attain

$$\begin{aligned} \left\| \widetilde{r}^{*}-\mathbb {T}\widetilde{r}^{*}\right\| \le \frac{1+K}{1-K}\sup _{r\in \mathbb {S}}\left\| \mathbb {T}r-\widetilde{ \mathbb {T}}r\right\| \text {.} \end{aligned}$$

(53)

Utilizing (51) in (53), we obtain

$$\begin{aligned} \left\| \widetilde{r}^{*}-\mathbb {T}\widetilde{r}^{*}\right\| \le \left( \frac{1+K}{1-K}\right) \epsilon \text {.} \end{aligned}$$

$\square$

Example 11

Let $\mathbb {S}$, $\mathbb {T}$ be as in Example 6 and $\widetilde{\mathbb {T}}$ be as in Example 9. Then, we have

$$\begin{aligned} \left| \mathbb {T}\widetilde{r}^{*}-\widetilde{r}^{*}\right|&=5.74492(-08) \\&\quad <5.43229(-05) \\&=\left( \frac{1+0.85}{1-0.85}\right) 4.40456(-06) \\&=\left( \frac{1+K}{1-K}\right) \epsilon . \end{aligned}$$

Now we can consider the following inverse problem:

Problem 1

For given $\varepsilon >0$ and a "target" $\overline{r}\in \mathbb { S}$, find a quasi-strictly contractive mapping $\mathbb {T}_{\varepsilon }$ with a unique fixed point $r_{\mathbb {T}_{\varepsilon }}^{*}=\mathbb {T} _{\varepsilon }\left( r_{\mathbb {T}_{\varepsilon }}^{*}\right)$ such that $\left\| \overline{r}-r_{\mathbb {T}_{\varepsilon }}^{*}\right\| \le \varepsilon$.

The inverse problem discussed in this context has its origins in early research on fractal image coding (see Fisher 1998). However, because of the intricate nature of fractal operators and their fixed point functions, discovering a contraction operator that reduces the approximation error $\left\| r-\overline{r}\right\|$ in fractal image coding to a minimum is an extremely challenging task. Indeed, Ruhl and Hartenstein (1997) demonstrated that this type of fractal image coding is NP-hard. As a result, fractal image coding methods have employed an alternative approach to the inverse problem that relies on the Collage theorem (Barnsley et al. 1986). These methods concentrate on locating a contraction operator $\mathbb {T}$ that minimizes the Collage distance $\left\| r-\mathbb {T}r\right\|$ instead. This minimization process is commonly known as Collage coding in the field on fractal coding.

The Collage Theorem 8 enables us to restate the inverse Problem 1 in the following more convenient form.

Problem 2

For given $\delta >0$ and a "target" $\overline{r}\in \mathbb {S}$, find a quasi-strictly contractive mapping $\mathbb {T}_{\delta }$ such that $\left\| \overline{r}-\mathbb {T}_{\delta }\overline{r}\right\| \le \delta$.

In other words, rather than seeking a quasi-strictly contractive mapping $\mathbb {T}_{\delta }$ that has fixed points near the target $\overline{r}\in \mathbb {S}$, we aim to find a quasi-strictly contractive mapping $\mathbb {T} _{\delta }$ that can map $\overline{r}\in \mathbb {S}$ to a point close to $\overline{r}$ itself.

Proposition 1

If there exists a solution to Problem 2, then there is also a solution to Problem 1.

Proof

Let $\varepsilon >0$ and $\overline{r}\in \mathbb {S}$ be given. For $\delta :=\left( 1-K\right) \varepsilon$, let $\mathbb {T}_{\delta }$ be a quasi-strictly contractive mapping with $\left\| \overline{r}-\mathbb {T} _{\delta }\overline{r}\right\| \le \delta$. If $\mathbb {T}_{\delta }\left( r_{\mathbb {T}_{\delta }}^{*}\right) =r_{\mathbb {T}_{\delta }}^{*}$, then Theorem 8 leads to

$$\begin{aligned} \left\| r_{\mathbb {T}_{\delta }}^{*}-\overline{r}\right\| \le \frac{1}{1-K}\left\| \overline{r}-\mathbb {T}_{\delta }\overline{r} \right\| \le \frac{1}{1-K}\delta =\varepsilon . \end{aligned}$$

$\square$

Example 12

Let’s consider the space $\mathbb {S}=C[0,1]$ equipped with the metric $\left\| r-s\right\| _{2}=\left( \int \limits _{S}\left( r\left( x\right) -s\left( x\right) \right) ^{2}dx\right) ^{1/2}$. Let $\delta =0.01$ and $\overline{r}\left( x\right) =0.4x^{2}+0.2x+0.3$ be the target. By using the method given in Levere et al. (2013), we find that $\mathbb {T}\left( r\left( x\right) \right) =\frac{2779}{9570}+\int \nolimits _{0}^{x}\left( \frac{420}{319}r\left( u\right) -\frac{27}{319}\right) du$ is a contraction mapping and thus a quasi-contractive mapping with the contractivity constant $K=\sqrt{\frac{826 }{953}}$. Indeed;

$$\begin{aligned} \left\| \mathbb {T}(r)-\mathbb {T}(s)\right\| _{2}^{2}= & {} \int \limits _{S}\left( \int \limits _{0}^{x}\left( \frac{420}{319}r\left( u\right) -\frac{27}{319}\right) du-\int \limits _{0}^{x}\left( \frac{420}{319} s\left( u\right) -\frac{27}{319}\right) du\right) ^{2}dx \\\le & {} \left( \frac{420}{319}\right) ^{2}\int \limits _{S}\left( \int \limits _{0}^{x}\left| r\left( u\right) -s\left( u\right) \right| du\right) ^{2}dx \\\le & {} \left( \frac{420}{319}\right) ^{2}\int \limits _{S}\left( \left( \int \limits _{0}^{x}du\right) ^{1/2}\left( \int \limits _{0}^{x}\left| r\left( u\right) -s\left( u\right) \right| ^{2}du\right) ^{1/2}\right) ^{2}dx \\\le & {} \left( \frac{420}{319}\right) ^{2}\int \limits _{S}\int \limits _{0}^{x}x\left| r\left( u\right) -s\left( u\right) \right| ^{2}dudx \\\le & {} \left( \frac{420}{319}\right) ^{2}\frac{1}{2}\int \limits _{S}\left| r\left( u\right) -s\left( u\right) \right| ^{2}du \\\le & {} \frac{826}{953}\left\| r-s\right\| _{2}^{2}. \end{aligned}$$

The mapping $\mathbb {T}$ has a fixed point $r_{\mathbb {T}}^{*}(x)=\frac{ 30293e^{\frac{420x}{319}}}{133,980}+\frac{9}{140}$ and $\left\| \overline{r }\left( x\right) -r_{\mathbb {T}}^{*}\left( x\right) \right\| _{2}=$ 0.00331 and $\left\| \overline{r}\left( x\right) -\mathbb {T} \left( \overline{r}\left( x\right) \right) \right\| _{2}=$ 0.00334 which satisfies followings

$$\begin{aligned} \left\| \overline{r}\left( x\right) -r_{\mathbb {T}}^{*}\left( x\right) \right\| _{2}= & {} 0.00331 \\\le & {} \frac{1}{1-\sqrt{\frac{826}{953}}}0.00334 \\= & {} 0.00354 \\= & {} \frac{1}{1-K}\left\| \overline{r}\left( x\right) -\mathbb {T}\left( \overline{r}\left( x\right) \right) \right\| _{2}. \end{aligned}$$

Figure 13 shows the graphs of $\overline{r}(x)$ and $r_{ \mathbb {T}}^{*}(x)$.

Fig. 13

The graphical representation of $\bar{r}(x)$ and $r^{*}_{\mathbb {T}} (x)$ for Example 12

5 Conclusion

The theorems presented in this article, specifically Theorems 2–4, complement the findings from (Usurelu et al. 2021). The stability and data dependency results from Theorems 5 and 6, respectively, are particularly noteworthy as they are obtained without any restrictions on the parametric sequences used in the TTP iteration algorithm. Consequently, these results represent significant improvements over the corresponding results from (Usurelu et al. 2021, Theorem 4.7) and (Usurelu et al. 2021, Theorem 4.8). As demonstrated in Example 1, the class of contraction mappings is a subset of the class of strictly-quasi contractive mappings. Consequently, the data dependency result presented in Theorem 7 is also a notable improvement over (Usurelu et al. 2021, Theorem 4.8). The results regarding the data dependency of fixed points, a form of stability, are highly relevant due to their potential for practical applications, and thereby deserve further investigation. For this reason, the paper introduces several collage theorems, which offer new insights into the data dependency of fixed points of strictly-quasi contractive mappings and furnish solutions to inverse problems associated with this class of mappings. Interestingly, it has been observed that the Collage theorems yield better estimates for the upper bound of the error in approximating $r^{*}$ by $\widetilde{r}^{*}$, i.e. $\left\| r^{*}-\widetilde{r}^{*}\right\|$, compared to the data dependency results. To demonstrate the effectiveness and applicability of all the results presented herein, a multitude of numerical examples are furnished, encompassing both linear and nonlinear differential equations (DEs) and partial differential equations (PDEs). This work serves as an important refinement and complement to the study by Usurelu et al (Int J Comput Math 98:1049–1068, 2021) and provides a more general framework for the analysis of quasi-strictly contractive mappings. The results obtained in this work have the potential to impact a wide range of fields, including mathematics, physics, and engineering.