Skip to main content
SpringerLink
Log in

First passage time and peak size probability distributions for a complex epidemic model

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract

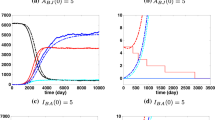
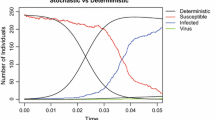
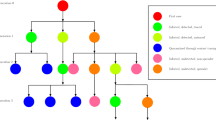
The potential of zoonotic diseases to cross-species physical boundaries makes them a persistent threat to global public health. Of all the zoonoses, the bubonic plague serves as a historical and modern model. In this work, we investigate a bubonic plague stochastic model using a continuous-time Markov chain (CTMC) model to study the disease dynamics in rats and humans. Using a Galton–Watson multi-type (GWbp) branching process, we have derived an analytical expression for disease extinction probability at the beginning of the epidemic. There is a variation in disease extinction probability calculated via the branching process and numerical simulations, which is the consequence of the discrete assumption of an infected flea instead of being considered in terms of an infected rat in the numerical simulation. An analytical expression for the distribution of first passage time (FPT) to spillover is also obtained in this work using the probability generating function (PGF) technique, and it agrees well with the FPT distribution obtained numerically. This distribution is defective since infected fleas can die before infecting human. Furthermore, the effect of the initial rat population on the FPT of spillover is also shown, which suggest that as the initial rat population increases, the likelihood of spillover decreases, and it increases as the rat population decreases. Additionally, we have derived an expression for the mean and variance of the first passage time to spillover, and we incorporate the impact of various parameters on the mean first passage time of spillover. Lastly, we have performed numerical simulations to estimate the peak size of each infected class and the related time to attain peak infection. The peak of the infected flea, which is a disease carrier, is much higher as compared to that of rat and human. Also, there is a delay in attaining peak size for the human population, which is the consequence of the human population being a secondary host for fleas to survive.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Data Availability Statement

Data sharing is not applicable to this article as no new data were created or analysed in this study.

References

  1. W.B. Karesh, A. Dobson, J.O. Lloyd-Smith, J. Lubroth, M.A. Dixon, M. Bennett, S. Aldrich, T. Harrington, P. Formenty, E.H. Loh et al., Ecology of zoonoses: natural and unnatural histories. The Lancet 380(9857), 1936–1945 (2012)

    Article  Google Scholar 

  2. J.O. Lloyd-Smith, D. George, K.M. Pepin, V.E. Pitzer, J.R.C. Pulliam, A.P. Dobson, P.J. Hudson, B.T. Grenfell, Epidemic dynamics at the human–animal interface. science 326(5958), 1362–1367 (2009)

    Article  ADS  Google Scholar 

  3. S. Singh, D.J. Schneider, C.R. Myers, Using multitype branching processes to quantify statistics of disease outbreaks in zoonotic epidemics. Phys. Rev. E 89(3), 032702 (2014)

    Article  ADS  Google Scholar 

  4. R. Coker, J. Rushton, S. Mounier-Jack, E. Karimuribo, P. Lutumba, D. Kambarage, D.U. Pfeiffer, K. Stärk, M. Rweyemamu, Towards a conceptual framework to support one-health research for policy on emerging zoonoses. Lancet. Infect. Dis 11(4), 326–331 (2011)

    Article  Google Scholar 

  5. W.B. Karesh, R.A. Cook, The human-animal link. Foreign Aff. 84, 38 (2005)

    Article  Google Scholar 

  6. L.J.S. Allen, V.L. Brown, C.B. Jonsson, S.L. Klein, S.M. Laverty, K. Magwedere, J.C. Owen, P. Van Den Driessche, Mathematical modeling of viral zoonoses in wildlife. Nat. Resour. Model. 25(1), 5–51 (2012)

    Article  MathSciNet  Google Scholar 

  7. M.J. Keeling, C.A. Gilligan, Metapopulation dynamics of bubonic plague. Nature 407(6806), 903–906 (2000)

    Article  ADS  Google Scholar 

  8. F. Gascuel, M. Choisy, J.-M. Duplantier, F. Débarre, C. Brouat, Host resistance, population structure and the long-term persistence of bubonic plague: contributions of a modelling approach in the Malagasy focus. PLoS Comput. Biol. 9(5), e1003039 (2013)

    Article  Google Scholar 

  9. World Health Organization et al. Human plague: review of regional morbidity and mortality, 2004–2009: introduction. Weekly Epidemiological Record= Relevé épidémiologique Hebdomadaire 85(06), 40–45 (2010)

  10. S. Chanteau, Atlas de la peste à Madagascar. IRD editions (2006)

  11. R.C. Ngeleja, L.S. Luboobi, Y. Nkansah-Gyekye, Modelling the dynamics of bubonic plague with yersinia pestis in the environment. Commun. Math. Biol. Neurosci., Article-ID (2016)

  12. R.R. Parmenter, E.P. Yadav, C.A. Parmenter, P. Ettestad, K.L. Gage, Incidence of plague associated with increased winter–spring precipitation in new Mexico. Am. J. Trop. Med. Hyg. 61(5), 814–821 (1999)

    Article  Google Scholar 

  13. W.E. Wingfield, S.B. Palmer, Veterinary Disaster Response (Wiley, New York, 2009)

    Google Scholar 

  14. C. McEvedy, The bubonic plague. Sci. Am. 258(2), 118–123 (1988)

    Article  Google Scholar 

  15. A.J. Nicholson, V.A. Bailey, The balance of animal populations—part I. In: Proceedings of the Zoological Society of London, vol. 105, pp. 551–598. Wiley Online Library (1935)

  16. K.R. Dean, F. Krauer, L. Walløe, O.C. Lingjærde, B. Bramanti, N.C. Stenseth, B.V. Schmid, Human ectoparasites and the spread of plague in Europe during the second pandemic. Proc. Natl. Acad. Sci. 115(6), 1304–1309 (2018)

    Article  ADS  Google Scholar 

  17. M.J. Keeling, C.A. Gilligan, Bubonic plague: a metapopulation model of a zoonosis. Proc. R. Soc. Lond. B 267(1458), 2219–2230 (2000)

    Article  Google Scholar 

  18. M. Buzby, D. Neckels, M.F. Antolin, D. Estep, Analysis of the sensitivity properties of a model of vector-borne bubonic plague. J. R. Soc. Interface 5(26), 1099–1107 (2008)

    Article  Google Scholar 

  19. J.E. Foley, J. Zipser, B. Chomel, E. Girvetz, P. Foley, Modeling plague persistence in host-vector communities in California. J. Wildl. Dis. 43(3), 408–424 (2007)

    Article  Google Scholar 

  20. J.A. Mwasunda, J.I. Irunde, D. Kajunguri, D. Kuznetsov, Outbreak or extinction of bovine cysticercosis and human taeniasis: a stochastic modelling approach. Appl. Math. Model. 106, 73–85 (2022)

    Article  MathSciNet  Google Scholar 

  21. T. Antal, P.L. Krapivsky, Exact solution of a two-type branching process: models of tumor progression. J. Stat. Mech.: Theory Exp. 2011(08), P08018 (2011)

    Article  Google Scholar 

  22. K.B. Athreya, P.E. Ney, K.B. Athreya, P.E. Ney, One Dimensional Continuous Time Markov Branching Processes. Branching Processes (Springer, Berlin, 1972), pp.102–136

    Google Scholar 

  23. N.T.J. Bailey, The Elements of Stochastic Processes with Applications to the Natural Sciences, vol. 25 (Wiley, New York, 1991)

    Google Scholar 

  24. J. Curran-Sebastian, L. Pellis, I. Hall, T. House, Calculation of Epidemic First Passage and Peak Time Probability Distributions. arXiv preprintarXiv:2301.07058 (2023)

  25. J.C. Miller, A primer on the use of probability generating functions in infectious disease modeling. Infect. Dis. Model. 3, 192–248 (2018)

    Google Scholar 

  26. B.-S. Chen, Z.-Y. Wu, Y.-J. Chen, J.-L. Chern, Data forecasts of the epidemic Covid-19 by deterministic and stochastic time-dependent models. arXiv preprint arXiv:2209.02880 (2022)

  27. Z.G. İşlier, R. Güllü, W. Hörmann, An exact and implementable computation of the final outbreak size distribution under Erlang distributed infectious period. Math. Biosci. 325, 108363 (2020)

    Article  MathSciNet  Google Scholar 

  28. H.E. Daniels, The maximum size of a closed epidemic. Adv. Appl. Probab. 6(4), 607–621 (1974)

    Article  MathSciNet  Google Scholar 

  29. J.R. Artalejo, A. Economou, M.J. Lopez-Herrero, The maximum number of infected individuals in sis epidemic models: computational techniques and quasi-stationary distributions. J. Comput. Appl. Math. 233(10), 2563–2574 (2010)

    Article  ADS  MathSciNet  Google Scholar 

  30. J. Amador, M. Lopez-Herrero, Cumulative and maximum epidemic sizes for a nonlinear seir stochastic model with limited resources. Discret. Contin. Dyn. Syst. Ser. B 23(8), 3137 (2018)

    MathSciNet  Google Scholar 

  31. J. Amador Pacheco, D. Armesto, A. Gómez-Corral, Extreme values in sir epidemic models with two strains and cross-immunity. Math. Biosci. & Engg. 16(4), 1992–2022 (2019). https://doi.org/10.3934/mbe.2019098

  32. C.J. Edholm, B.O. Emerenini, A.L Murillo, O. Saucedo, N. Shakiba, X. Wang, L.J.S. Allen, A. Peace, Searching for superspreaders: Identifying epidemic patterns associated with superspreading events in stochastic models. Understanding complex biological systems with mathematics, p. 1–29 (2018)

  33. O. Diekmann, J.A.P. Heesterbeek, M.G. Roberts, The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 7(47), 873–885 (2010)

    Article  Google Scholar 

  34. P. Van den Driessche, J. Watmough, Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 180(1–2), 29–48 (2002)

    Article  MathSciNet  Google Scholar 

  35. P. Sarathi Mandal, S. Maity, Impact of demographic variability on the disease dynamics for honeybee model. Chaos Interdiscip. J. Nonlinear Sci. 32(8), 083120 (2022)

    Article  MathSciNet  Google Scholar 

  36. L.J.S. Allen, A primer on stochastic epidemic models: formulation, numerical simulation, and analysis. Infect. Dis. Model. 2(2), 128–142 (2017)

    Google Scholar 

  37. M. Maliyoni, Probability of disease extinction or outbreak in a stochastic epidemic model for West Nile virus dynamics in birds. Acta. Biotheor. 69(2), 91–116 (2021)

    Article  Google Scholar 

  38. M. Maliyoni, F. Chirove, H.D. Gaff, K.S. Govinder, A stochastic tick-borne disease model: exploring the probability of pathogen persistence. Bull. Math. Biol. 79, 1999–2021 (2017)

    Article  MathSciNet  Google Scholar 

  39. M. Maliyoni, F. Chirove, H.D. Gaff, K.S. Govinder, A stochastic epidemic model for the dynamics of two pathogens in a single tick population. Theor. Popul. Biol. 127, 75–90 (2019)

    Article  Google Scholar 

  40. S. Maity, P.S. Mandal, A comparison of deterministic and stochastic plant–vector–virus models based on probability of disease extinction and outbreak. Bull. Math. Biol. 84(3), 41 (2022)

    Article  MathSciNet  Google Scholar 

  41. R.J. Eisen, A.P. Wilder, S.W. Bearden, J.A. Montenieri, K.L. Gage, Early-phase transmission of Yersinia pestis by Unblocked Xenopsylla cheopis (Siphonaptera: Pulicidae) is as efficient as transmission by blocked fleas. J. Med. Entomol. 44(4), 678–682 (2007)

    Article  Google Scholar 

  42. L.A. White, L. Mordechai, Modeling the justinianic plague: comparing hypothesized transmission routes. PLoS (30 Apr. 2020) (2020)

  43. S. Hautphenne, Extinction probabilities of supercritical decomposable branching processes. J. Appl. Probab. 49(3), 639–651 (2012)

    Article  MathSciNet  Google Scholar 

  44. S. Hautphenne, G. Latouche, G. Nguyen, Extinction probabilities of branching processes with countably infinitely many types. Adv. Appl. Probab. 45(4), 1068–1082 (2013)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

Suman Kumari’s research is supported by research fellowship from MHRD, Government of India, Partha Sarathi Mandal’s research is supported by CSIR Project [File No: 25(0303)/19/EMR-II].

Author information

Authors and Affiliations

  1. Department of Mathematics, NIT Patna, Patna, Bihar, 800005, India

    Suman Kumari, Partha Sarathi Mandal & Moitri Sen

Authors
  1. Suman Kumari
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Partha Sarathi Mandal
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Moitri Sen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Partha Sarathi Mandal.

Ethics declarations

Conflict of interest

The authors have no conflicts to disclose.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kumari, S., Mandal, P.S. & Sen, M. First passage time and peak size probability distributions for a complex epidemic model. Eur. Phys. J. Plus 139, 324 (2024). https://doi.org/10.1140/epjp/s13360-024-05108-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/s13360-024-05108-z

Search

Navigation