Financial sustainability and automatic balance mechanisms for NDC pension systems with disability benefits

Abstract

The need for Long term care (LTC) service continues to rise due to the increasing number of elderly in the world, which stresses the healthcare systems. As most of the LTC recipients are over age 65, several authors studied retirement products combining a lifetime annuity with a long-term care benefit (typical examples are Enhanced Pension and Life Care Annuity). The development of an integrated strategy may help to address the issue of the cost of care for pensioners affected by disability. In this paper, we contribute to the debate on the introduction of LTC benefits into a notional defined contribution (NDC) pension system by using a multivariate stochastic model to represent the future evolution of transition probabilities and economic variables, which allows investigation of the financial sustainability of the system in a stochastic environment. The presence of LTC adds new risk elements, such as the uncertainty related to disability rates and mortality rates of the disabled, which may jeopardize the financial equilibrium of the integrated system. To restore the system’s equilibrium, we apply two types of automatic balance mechanisms (ABM), one based on the solvency ratio, and the other on the liquidity ratio. Both act on the indexation of pensions and the notional rate.

1 Introduction

An increasing number of countries—Italy included—are affected by the ageing population, which has raised growing concern both for the sustainability of the social security system and for the system’s ability to extend coverage to new emerging socioeconomic risks, such as the need to receive long-term care (LTC) in old age. LTC expenditure is expected to grow significantly in the next years in advanced countries. In Italy, the LTC public spending was 1.7% of GDP in 2019 and will rise to 1.9% in 2030 and 2.6% in 2050 based on the EU projections (European Commission, 2021).

Population ageing and socioeconomic risks call for the creation of a collective LTC coverage. It can be achieved either by a social security system (public first pillar) or an occupational scheme (second pillar). We focus on developing an LTC coverage mechanism in a social security arrangement. The main reasons for implementing such coverage are cost reduction, uncertainty lowering, increase in efficiency, increase in the perception of LTC need, and moral hazard reduction (see Pla-Porcel et al. (2016), which collected the main arguments listed in the literature in an exhaustive list). As the majority of the LTC recipients are aged over 65—based on the OECD (2019) data 78% of LTC recipients on average across the OECD countries were older than 65 in 2017—it appears natural to link a public LTC coverage to retirement pensions. The development of an integrated strategy could help Governments to address the issue related to the cost of care for pensioners affected by disability. As observed by Brown and Warshawsky (2013), the integration would allow the inclusion of most of the population currently rejected by underwriting, those in poor health or lifestyles but who would not go immediately into long-term care claims and who also have a lower life expectancy.

Some scholars studied retirement products combining a lifetime annuity with an LTC benefit: typical examples are Enhanced Pension (Pitacco, 1995) and Life Care Annuity (Murtaugh et al., 2001; Brown & Warshawsky, 2013). Other scholars have addressed the idea of combining retirement with LTC benefits. For example, Chen (1994) proposed the creation of a social insurance program to provide basic LTC coverage by diverting a small portion of a retiree’s social security cash benefits for LTC; Costa-Font et al. (2014) observed that LTC financing needs to be considered as part of an overall retirement strategy rather than just a simple extension of health insurance, even if one can separate the goals of consumption smoothing (retirement) from insurance (LTC); Ventura-Marco and Vidal-Meliá (2014) proposed an actuarial balance sheet model for defined benefit pay-as-you-go pension systems with disability and retirement contingencies; Ventura-Marco and Vidal-Meliá (2016) explored the idea of integrating old-age and permanent disability into a generic notional defined contribution (NDC) framework; Pla-Porcel et al. (2016) embedded life care annuities in an NDC framework by developing a multistate overlapping generations model that includes the so-called survivor dividend; Vidal-Meliá et al. (2020) extended the proposal of Pla-Porcel et al. (2016) by considering both an LTC benefit as a function of the annuitant’s degree of disability and a minimum pension.

Most of the authors mentioned above refer to NDC pension systems. The philosophy of the NDC systems has been successfully implemented in different European countries (Sweden, Italy, Poland, Latvia...) essentially for actuarial fairness, which directly links contributions to pensions and for the defined contribution nature that should induce financial sustainability in the long-term. However, in realistic conditions, an NDC system cannot automatically guarantee financial sustainability, being vulnerable to both demographic and economic shocks. Applying automatic balance mechanisms (ABMs) may be necessary to restore the equilibrium of the system, avoiding the legislator from repeatedly intervening in the pension system through dedicated laws.

The presence of LTC benefits adds new risk elements to the system, such as the uncertainty related to disability rates and mortality rates of the disabled. In fact, as noted by Levantesi and Menzietti (2012), stand-alone LTC annuities are characterized by a higher risk than life annuities.¹ However, introducing LTC benefits into a pension system could produce diversification benefits as longevity and morbidity risks work in opposite directions, generating natural hedging (Rickayzen, 2007). In this regard, Levantesi and Menzietti (2018) studied how to obtain an optimal mix of LTC benefits and life annuities to reduce the insurance portfolio risk. In conclusion, on one hand, the introduction of LTC benefits could increase the risk of the NDC system due to new sources of uncertainty, on the other hand, it could result in a risk reduction if the weight of LTC benefits over life annuities was such as to produce natural hedging. However, as also noted by Pla-Porcel et al. (2016) in the conclusion of their paper, in an NDC system with LTC benefits it would be necessary to introduce ABMs to re-establish the sustainability of the system.

The contribution of this paper to the debate on the introduction of LTC benefits into a pension system is twofold. First, we analyze the pension system’s financial sustainability in a stochastic environment, taking into account both biometric (longevity and disability) and economic risks. We use a multivariate stochastic model to represent the future evolution of mortality and disability transition probabilities, which allows us to provide confidence intervals that capture the projections’ uncertainty. We also follow a stochastic approach to model the main economic variables involved in the system. We develop a forward-looking simulation analysis using 5,000 paths. Secondly, we include two types of ABM in an integrated LTC-NDC system, one based on the solvency ratio, and the other on the liquidity ratio, both acting on the indexation of pensions and notional rate (these two ABMs have been applied by Alonso-García et al. (2018) to a classical NDC system).

The NDC framework we used throughout the paper is inspired by the current Italian NDC system. The macroeconomic and demographic data come from official Italian data sources.

The rest of the paper is organized as follows. Section 2 introduces the basics of an NDC pension system providing both a retirement pension and an LTC benefit. Section 3 provides the equilibrium condition in a PAYG scheme and presents the ABMs used to restore the financial equilibrium of the system. Section 4 illustrates the modelling of macroeconomic and demographic variables. Section 5 provides a numerical illustration of the model applied to the Italian NDC pension system. Finally, Sect. 6 concludes the paper.

2 An NDC system with LTC benefit

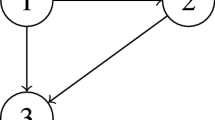
We consider an NDC pension system paying only old-age retirement and LTC benefits, disregarding invalidity benefits, survivor benefits, and withdrawals. Contributions and benefits are paid yearly in advance. Disability benefits are paid only after retirement. The population is divided into four different states to which each individual may belong: contributor (1), pensioner (2), disabled (3), and dead (4). The transition probabilities between states depend on age and time. This implies that the eligibility for pension benefits is independent of the years of service. States and possible transitions are illustrated in Fig. 1.

Fig. 1

Multiple state model for our system

We define the transition probability of an individual aged x in state i at time t to arrive in state j at time $t+h$ as $_{h}p^{ij}(x,t)$, and the probability for the same individual to remain in state i for time h as $_{h}p^{ii}(x,t)$.

The scope of an LTC benefit is to financially support individuals becoming dependent and needing care (disabled) to pay for care services. Therefore, our model includes an LTC benefit in the form of an enhanced retirement pension, $b^{3}$, which directly increases the retirement pension received in the healthy state, $b^{2}$, when the pensioner becomes disabled. This enhanced amount should help the disabled pensioner to satisfy his/her need for care services. We consider only one level of disability and neglect recovery from disability. This assumption is coherent with the empirical evidence from our data, which presents a 3.4% average annual rate of decrements other than death in the reference period. This is a consequence of the type of LTC benefits allowed by the Italian National Institute of Social Security only paid to individuals with severe disability. Specifically, we deal with two different types of LTC annuity: life care annuity (LCA) and enhanced pension annuity (EPA).

• In the LCA, the LTC benefit $b^{3}$ is obtained by a percentage increase, $\eta$, of the basic NDC pension, b: $b^{3}=b(1+\eta )$, while the pension received in the healthy state, $b^{2}$, is equal to the basic NDC pension, b. The uplift is financed during the accumulation period with an extra contribution.

• In the EPA, the uplift is financed with a reduction of the pension received in the healthy state: $b^{3}=b^{2}(1+\eta )$, with $b^{2}<b<b^{3}$.

In the following, we describe the main features of our model focusing on the population dynamics, contributions, and benefits, and dealing with the system’s financial sustainability.

Population dynamics. Let denote $N^{k}(x,t)$ the number of individuals in state k at age x at time t and $Z^{k}(x,t)$ the new entrants. The demographic dynamics at each time t is represented by:

$$\begin{aligned} N^{k}(x,t)=N^{k}(x-1,t-1) p^{kk}(x-1,t-1)+Z^{k}(x,t)\quad k=1,2,3,4 \end{aligned}$$

(2.1)

The total population in the state k at time t is given by $N^{k}(t)= \sum _{x} N^{k}(x,t)$. The population evolution illustrated in Eq. 2.1 indicates that the population at time t depends both on the previous-year population who is still in state k by time t and the new entrants in state k aged x in year t, $Z^{k}(x,t)$.

Denoting $x_r$ the retirement age, the number of new healthy pensioners aged $x_r$ in year t can be obtained as:

$$\begin{aligned} Z^{2}(x_r,t)=N^{1}(x_r-1,t-1)p^{12}(x_r-1,t-1) \end{aligned}$$

(2.2)

while, the number of new disabled pensioners aged $x>x_r$ in year t as:

$$\begin{aligned} Z^{3}(x,t)=N^{2}(x-1,t-1) p^{23}(x-1,t-1) \quad \text {for}\quad x>x_r \end{aligned}$$

(2.3)

Finally, the number of new deaths aged x occurring in the year t is given by:

$$\begin{aligned} Z^{4}(x,t)=\sum _{k=1}^{3} N^{k}(x-1,t-1) p^{k4}(x-1,t-1) \end{aligned}$$

(2.4)

Note that the quantities calculated in the previous Eqs. 2.1–2.4 are expected values. With reference to the future evolution of individuals in the active state, we opted to estimate them by assuming known the growth rate of the total active population in each projection year, $\rho (t)$, together with the relative distribution by sex and age of new entrants, $d^{1}_{z}(x,t)$ (see Iyer (1999) for further details on alternative methods). Under this assumption, the future evolution of individuals in the active state, given the initial number $N^{1}(0)$ of total active population, is obtained by:

$$\begin{aligned} N^{1}(t)=N^{1}(t-1)(1+\rho (t)) \end{aligned}$$

(2.5)

The total number of new actives at time t depends on the evolution of the active population and is calculated as follows:

$$\begin{aligned} Z^{1}(t)=N^{1}(t)-\sum _{x} N^{1}(x-1,t-1) p^{11}(x-1,t-1) \end{aligned}$$

(2.6)

On one hand, this approach has the advantage of making it possible to represent the evolution of the active working population taking into account the development of the demand for labour. On the other hand, this choice has the drawback that, in case of a negative $\rho (t)$ (which is possible), it could lead to a negative number of new entries, $Z^{1}(t)$. On this point, it should be noted that negative values of $\rho (t)$ do not automatically lead to negative $Z^{1}(t)$ values: actually, the total active population is reduced each year for new retirements, so a positive number of new entrants is obtained even with $\rho (t)$ negative. A negative value of new entrants is achieved only for $\rho$ values such that a reduction in the total active population is greater than that produced by the new pensioners.

In order to avoid negative values for Z, a non-negativity constraint should be added. We observe that, under the assumptions and parameters adopted in the following numerical application, the values assumed by $\rho (t)$ are never such as to produce a negative $Z^{1}(t)$. Therefore, in the numerical application, the non-negativity constraint never acts.

Once $Z^{1}(t)$ has been determined, the number of new actives at time t aged x is calculated by considering the relative age distributions as follows:

$$\begin{aligned} Z^{1}(x,t)=Z^{1}(t) d^{1}_{z}(x,t) \quad \text {for}\,\, x<x_r \end{aligned}$$

(2.7)

where $d^{1}_{z}(x,t)$ is the relative age distribution of the new entrants in state 1.

Contributions and benefits. Let denote s(x, t, i) as the wage for the i-th active aged x at time t, assuming the same wage for all the individuals belonging to the same generation, $s(x,t,i)=s(x,t)$ for all i, independently of their past service duration. The individual wage evolves as follows:

$$\begin{aligned} s(x,t)=s(x,t-1) \left[ 1+\xi (t)\right] \quad \text {for}\,\, x<x_r \end{aligned}$$

(2.8)

where $\xi (t)$ is the growth rate of individual wage from $t-1$ to t. Therefore, we implicitly assumed that $\xi (t)$ is the same for any age x. The individual wage multiplied by the number of actives for the same age x and time t provides the total wage earned by the active population aged x at time t:

$$\begin{aligned} S(x,t)=N^{1}(x,t) s(x,t) \quad \text {for}\,\, x<x_r \end{aligned}$$

(2.9)

Denoting $S(t)= \sum _{x} S(x,t)$ as the total wage at time t, the corresponding average wage is:

$$\begin{aligned} s(t)=\frac{S(t)}{N^{1}(t)} \end{aligned}$$

(2.10)

Denoting c(t) as the contribution rate of the pension system at time t, the individual contribution paid by an active aged x at time t is:

$$\begin{aligned} c(x,t)= c(t) s(x,t) \quad \text {for}\,\, x<x_r \end{aligned}$$

(2.11)

The total contribution for the active population aged x at time t is given by:

$$\begin{aligned} C(x,t)= N^{1}(x,t) c(x,t) = c(t) S(x,t) \quad \text {for}\,\, x<x_r \end{aligned}$$

(2.12)

Finally, the amount of total contribution earned by the system at time t is:

$$\begin{aligned} C(t)= \sum _{x} C(x,t) = c(t) S(t) \end{aligned}$$

(2.13)

An NDC system is characterized by a "defined-contribution" design, therefore the contribution rate is fixed and assumed constant over time, $c(t)=c$ for all t. The contributions of each participant are noted on an individual notional account and are remunerated each year t at a common rate of return, g(t). Differently from a defined contributions scheme, in an NDC system, contributions are not invested in the financial market, and g(t) is a notional rate established in the design to assure the financial stability of the system.²

The individual notional account for an active i aged x at the end of year t evolves as follows:

$$\begin{aligned} m(x,t,i)= \left[ m(x-1,t-1,i) + c(x,t)\right] \left[ 1+g(t)\right] \quad \text {for}\,\, x<x_r \end{aligned}$$

(2.14)

At retirement, the initial benefit is determined by converting the individual notional account into an annuity consistently with the remaining cohort life expectancy, the expected indexation rate, $\lambda ^{*}$, and the expected rate of return, $g^{*}$. Therefore, the initial benefit (paid yearly in advance) calculated for a new pensioner i at the retirement age $x_r$ is:

$$\begin{aligned} b(x_r,t,i)=\frac{m(x_r,t,i)}{(x_r,t)} \end{aligned}$$

(2.15)

where $(x_r,t)$ is the annuity rate, which in our framework is defined as follows:

$$\begin{aligned} (x_r,t)=\sum _{h}\,\left[ _{h}p^{22*}(x_r,t)+_{h}p^{23*}(x_r,t)\right] \cdot \prod _{k=t}^{t+h}\left[ 1+j^{*}(k)\right] ^{-1} \end{aligned}$$

(2.16)

with $_{h}p^{22*}(x,t)$ and $_{h}p^{23*}(x,t)$ are the theoretical or ex-ante probabilities of a healthy pensioner aged x at time t to stay in state 2 for h years and state 3 after h years, respectively (in the numerical application, they are determined as a point forecast of the rates), and $j^{*}(k)=\frac{1+g^{*}(k)}{1+\lambda ^{*}(k)}-1$ is a rate measuring the amount by which the notional rate deviates from pension indexation (Gronchi and Nisticó 2006).

The annuity rate $(x_r,t)$ could be decomposed in two parts: $(x_r,t)=^{22}(x_r,t)+^{23}(x_r,t)$ with:

$$\begin{aligned} ^{22}(x_r,t)=\sum _{h}\,_{h}p^{22*}(x_r,t)\cdot \prod _{k=t}^{t+h}\left[ 1+j^{*}(k)\right] ^{-1} \end{aligned}$$

(2.17)

$$\begin{aligned} ^{23}(x_r,t)=\sum _{h}\,_{h}p^{23*}(x_r,t)\cdot \prod _{k=t}^{t+h}\left[ 1+j^{*}(k)\right] ^{-1} \end{aligned}$$

(2.18)

Similarly, the annuity rate for a new disabled pensioner aged $x \ge x_r$ at time t is determined by:

$$\begin{aligned} ^{23}(x,t)=\sum _{h}\,_{h}p^{23*}(x,t)\cdot \prod _{k=t}^{t+h}\left[ 1+j^{*}(k)\right] ^{-1} \quad \text {for}\,\, x \ge x_r \end{aligned}$$

(2.19)

Life Care Annuity (LCA). In the case of LCA benefits, the pension amount, $b^2$, paid to a new (healthy) pensioner, is calculated as:

$$\begin{aligned} b^2(x_r,t,i)=\frac{m'(x_r,t,i)}{^{22}(x_r,t)+(1+\eta ) ^{23}(x_r,t)} \end{aligned}$$

(2.20)

where $m'(x_r,t,i)$ is the value of the notional amount to be accumulated to finance both the old-age pension and LCA benefit (with $m'(x_r,t,i)> m(x_r; t; i)$). From Eq. 2.20 and considering Eq. 2.15 and that $b^2(x_r,t,i)$ is equal to $b(x_r,t,i)$, the basic pension amount in an NDC system without LTC, we obtain the following expression of $m'(x_r,t,i)$:

$$\begin{aligned} \begin{aligned} m'(x_r,t,i)&= b^2(x_r,t,i)\left[ ^{22}(x_r,t)+^{23}(x_r,t)\right] +\eta b^2(x_r,t,i)^{23}(x,t)\\&= m(x_r,t,i)+\eta b^2(x_r,t,i)^{23}(x,t) \end{aligned} \end{aligned}$$

(2.21)

where the quantity $\eta b(x_r,t,i)^{23}(x,t)$ represents the cost of the enhancement with respect to the basic pension amount. The extra benefit paid in case of disability is financed by an additional contribution. The total enhanced contribution during the active life ($x<x_r$) is determined as:

$$\begin{aligned} c'(t) = c(t) \frac{^{22}(x_r,t)+(1+\eta )^{23}(x_r,t)}{^{22}(x_r,t)+^{23}(x_r,t)} \end{aligned}$$

(2.22)

One important point must be stressed. In a traditional NDC, the contribution rate c(t) being constant, an increase in life expectancy leads to a reduction in pension amount (see the third term in 2.20). If $c(t)=c \quad \forall t$, from 2.21 (or from Eq. 2.22), it can be verified that $c'(t)$ remains constant only provided that ratio $\frac{^{22}(x_r,t)+(1+\eta )^{23}(x_r,t)}{^{22}(x_r,t)+^{23}(x_r,t)}$ remains steady over time, which typically does not occur. To overcome this issue and continue to have $c'(t)=c' \quad \forall t$, two solutions can be adopted: it can be assumed that $\eta$ may vary over time to leave the ratio constant, or an average $c'$ on the projection horizon can be determined to verify the long-term equilibrium of the pension system. In the following numerical application, we have adopted the second approach.

When introducing the LCA, we define $C'(x,t)$ and $C'(t)$ consistently with C(x, t) and C(t).

The total benefits paid to the new healthy and disabled pensioners in the year t are respectively given by:

$$\begin{aligned} B^{2}_z(x_r,t)&= \sum _{i \in Z^{2}(x_r,t)} b(x_r,t,i)\end{aligned}$$

(2.23)

$$\begin{aligned} B^{3}_z(x,t)&= (1+\eta ) \sum _{i \in Z^{3}(x,t)} b(x,t,i) \quad \text {for}\quad x>x_r \end{aligned}$$

(2.24)

Enhanced Pension Annuity (EPA). In the case of the EPA benefits, the following relation holds:

$$\begin{aligned} b(x_r,t,i)\left[ ^{22}(x_r,t)+^{23}(x_r,t)\right] =b^{2}(x_r,t,i)^{22}(x_r,t)+b^{3}(x,t,i)^{23}(x_r,t) \end{aligned}$$

(2.25)

with $b^{3}(x,t,i)=b^{2}(1+\eta )$ and $b^{2}<b<b^{3}$.

The initial benefit for a new (healthy) pensioner is:

$$\begin{aligned} b^{2}(x_r,t,i)=\frac{m(x_r,t,i)}{^{22}(x_r,t)+(1+\eta )^{23}(x_r,t)} \end{aligned}$$

(2.26)

The total benefits paid to the new healthy and disabled pensioners in the year t are respectively given by:

$$\begin{aligned} B^{2}_{z}(x_r,t)&= \sum _{i \in Z^{2}(x_r,t)} b^{2}(x_r,t,i)\end{aligned}$$

(2.27)

$$\begin{aligned} B^{3}_z(x,t)&= (1+\eta ) \sum _{i \in Z^{3}(x,t)} b^{2}(x,t,i) \quad \text {for}\quad x>x_r \end{aligned}$$

(2.28)

In both the LCA and EPA, the basic pension amount at a certain time is equal to that earned at the previous time, increased by the indexation rate, $\lambda$³:

$$\begin{aligned} b(x,t)= b(x-1,t-1) \left[ 1+\lambda (t-1)\right] \quad \text {for}\quad x>x_r \end{aligned}$$

(2.29)

The pension indexation rate in year t is usually based on wage growth rate $\xi (t)$ (as e.g. in Sweden) or on inflation rate, that hereafter we denote with i(t) (as e.g. in Italy). In the first case, average pensions have the same evolution as average wages; in the second case, the evolution of average pensions is lower than average wages.

The total pensions paid to all retirees aged x in the year t evolve as follows:

$$\begin{aligned} B^2(x,t)&= B^2(x-1,t-1) p^{22}(x-1,t-1) \left[ 1+\lambda (t-1)\right] \quad \text {for}\quad x>x_r \end{aligned}$$

(2.30)

$$\begin{aligned} B^3(x,t)&= B^3(x-1,t-1) p^{33}(x-1,t-1) \left[ 1+\lambda (t-1)\right] + B^3_{z}(x,t) \quad \text {for}\quad x>x_r \end{aligned}$$

(2.31)

Denoting $B(t)= \sum _{x,i} B^i(x,t)$ with $i=2,3$ the amount of total pensions paid to all retirees in the year t, the corresponding average pension $\bar{b}(t)$ is:

$$\begin{aligned} \bar{b}(t)=\frac{B(t)}{N^{2}(t)+N^{3}(t)} \end{aligned}$$

(2.32)

To summarize, the main parameters of the proposed pension system are:

• The contribution rates c(t) and $c'(t)$ (fixed due to the DC structure),

• The notional rate g(t), and the indexation rate $\lambda (t)$,

• The retirement age $x_r$ (assumed constant over time),

• The conversion factors $^{22}(x_r,t)$ and $^{23}(x_r,t)$, transforming the notional account into lifetime annuities.

3 Equilibrium contribution rate, financial sustainability and ABMs

The equilibrium contribution rate. In a balanced PAYG scheme, income from contributions⁴ is equal to expenditure on pensions. Therefore, the system is in equilibrium in year t when:

$$\begin{aligned} C(t)=B(t) \end{aligned}$$

(3.1)

We define the implicit contribution rate as the rate satisfying the system’s equilibrium equation 3.1 as:

$$\begin{aligned} \hat{c}(t)= \frac{B(t)}{S(t)} \end{aligned}$$

(3.2)

In a PAYG system, the contributions effectively paid to the system each year t depend on a constant contribution rate $c(t)=c$, therefore Eq. 2.13 becomes $C(t)=c \cdot S(t)$, which combined with Eq. 3.2 gives rise to the following expression:

$$\begin{aligned} \hat{c}(t)=c \cdot \frac{B(t)}{C(t)} \end{aligned}$$

(3.3)

When the pension system is in equilibrium in year t (Eq. 3.1), from Eq. 3.3 we find that $\hat{c}(t)=c$, otherwise $\hat{c}(t)\gtrless c$. In the latter case, especially when the equilibrium condition does not verify for at least some consecutive years, it may be necessary to act on the pension system to restore balance.

Now, by combining Eqs. 2.10 and 2.13, we can express C(t) as $N^{1}(t) \cdot c(t) \cdot s(t)$, and, considering Eq. 2.32, we can write B(t) as $\left[ N^{2}(t)+N^{3}(t)\right] \cdot \bar{b}(t)$. Therefore, the equilibrium Eq. 3.1 becomes:

$$\begin{aligned} N^{1}(t) \cdot c(t) \cdot s(t) = \left[ N^{2}(t)+N^{3}(t)\right] \cdot \bar{b}(t) \end{aligned}$$

(3.4)

From Eq. 3.4, we can derive the following expression of the equilibrium contribution rate:

$$\begin{aligned} \hat{c}(t)=\frac{N^{2}(t)+N^{3}(t)}{N^{1}(t)} \cdot \frac{\bar{b}(t)}{s(t)} \end{aligned}$$

(3.5)

The ratio $\frac{N^{2}(t)+N^{3}(t)}{N^{1}(t)}$, measuring the proportion of the pensioners over the active population, is usually called dependency ratio and will be denoted as D(t) in the following. The ratio $\frac{\bar{b}(t)}{s(t)}$ is the average replacement rate of the system in the year t that we denote as r(t). Consequently, Eq. 3.5 can be rewritten as:

$$\begin{aligned} \hat{c}(t)=D(t) \cdot r(t) \end{aligned}$$

(3.6)

Demographic evolution and/or economic dynamics could undermine the PAYG equilibrium in Eq. 3.1. While in a pure Defined Benefit-PAYG system, being the benefits fixed, the equilibrium can be restored through a change of the contribution rate, in an NDC system, where the contribution rate should be constant, the equilibrium is obtained by changing (usually reducing) the replacement rate. This is automatically obtained through the notional rate change, linked to the economic conditions, and variation in the expected probabilities in Eq. 2.16, reflecting life expectancy evolution. But, as observed by Devolder et al. (2021), there are situations where an NDC system is not able to immediately restore the equilibrium, thus remaining vulnerable to demographic and economic shocks. These situations may require the application of an ABM.⁵

The financial sustainability condition. A PAYG system could experience periods with a cash-flow deficit when $C(t)<B(t)$, producing a pension liability, or periods with a surplus, when $C(t)>B(t)$, implying the accumulation of a reserve fund F(t). The evolution of the reserve fund F(t) in $t \in [0,T]$ where T is the end of a fixed time horizon, with $F(t)\gtreqless 0$, is given by:

$$\begin{aligned} F(t)= F(t-1) \left[ 1+g(t-1)\right] +C(t)-B(t) \end{aligned}$$

(3.7)

where the rate of return of the reserve fund is assumed to be equal to the notional rate, g.⁶

Generally, the financial sustainability of a pension system is assessed in terms of the Net Present Value of income from contributions and pension expenditures on a predefined (long) time horizon, NPV(0, T) (see e.g., Godinez-Olivares et al. (2016)):

$$\begin{aligned} NPV(0,T)=\sum _{t=1}^{T}{C(t)\prod _{h=0}^{t-1}\left[ 1+g(h)\right] ^{-1}}- \sum _{t=1}^{T}{B(t)\prod _{h=0}^{t-1}\left[ 1+g(h)\right] ^{-1}} \end{aligned}$$

(3.8)

A pension system can be considered sustainable if the NPV over a predefined time horizon T is not negative, $NPV(0,T)\ge 0$. It is worth noting that T must be a long time. The actuarial balance of social security programs usually considers a time horizon of at least 75 years. This is the case of, e.g., the U.S. and Canada, while Japan adopts a time horizon of 95 years (Vidal-Meliá et al., 2009). It is interesting to note that the financial sustainability condition expressed as a function of NPV can be formulated in terms of reserve fund: it is possible to demonstrate that, assuming $F(0)=0$, the condition $NPV(0,T)\ge 0$ is equivalent to require that $F(T)\ge 0$.

In the following, we measure the financial sustainability of the system by the value of the reserve fund at the end of the time horizon, T. Therefore, a pension system can be considered financially sustainable if:

$$\begin{aligned}F(T)\ge 0\end{aligned}$$

ABMs. Following (Alonso-García et al., 2018), we consider two ABMs, one based on liquidity ratio and the other on solvency ratio. We define the liquidity ratio LR(t) and the solvency ratio SR(t) in a generic year t respectively as follows:

$$\begin{aligned} LR(t)&=\frac{C(t)+F^{-}(t)}{B(t)} \end{aligned}$$

(3.9)

$$\begin{aligned} SR(t)&=\frac{CA(t)+F^{-}(t)}{M(t)+V(t)} \end{aligned}$$

(3.10)

where CA(t) are the contribution assets that we calculate as:

$$\begin{aligned} CA(t)=C(t) TD(t) \end{aligned}$$

(3.11)

where TD(t) is the turnover duration, which represents the "average time a unit of money is in the system" (Palmer, 2006) in a stable economic, demographic and legal environment. TD(t) is calculated as the difference between the weighted average age of pensioners, $A^r(t)$, and the weighted average age of contributors, $A^c(t)$ (see Boado-Penas and d. C., Valdés-Prieto, S., Vidal-Meliá, C. (2008) for more details):

$$\begin{aligned} TD(t)=A^r(t)-A^c(t) \end{aligned}$$

(3.12)

where:

$$\begin{aligned} A^r(t)=\frac{\sum _{x}\left[ (B^2(x,t)+B^5(x,t)\right] x}{B(t)} \end{aligned}$$

(3.13)

and:

$$\begin{aligned} A^c(t)=\frac{\sum _{x} C(x,t)x}{C(t)} \end{aligned}$$

(3.14)

$F^{-}(t)$ is the reserve fund in the year t before contributions and benefit payments:

$$\begin{aligned} F^{-}(t)=F(t)-C(t)+B(t), \end{aligned}$$

M(t) is the total notional amount for the contributors calculated as:

$$\begin{aligned} M(t)= \sum _{x} \sum _{i \in N^{1}(x,t)} m(x,t,i),\end{aligned}$$

and finally, V(t) is the expected value of the total reserve for pensioners at time t:

$$\begin{aligned} V(t)=\sum _{k\in 2,3}N^{k}(x,t) v^{k}(x,t) b^{k}(t),\end{aligned}$$

where $v^{k}(x,t)=^{2k}(x,t)$ is the individual reserve rate of a pensioner in state k aged x in the year t.

The ABM for the liquidity ratio (solvency ratio) is designed to achieve a liquidity ratio (solvency ratio) equal to 1. We denote LR-ABM the ABM based on the liquidity ratio, and SR-ABM based on the solvency ratio. Both of them can be symmetric or asymmetric. The symmetric LR-ABM (SR-ABM) decreases pensions and notional amounts when $LR(t)<1$ ($SR(t)<1$), and increases pensions and notional amounts when $LR(t)>1$ ($SR(t)>1$). While the asymmetric LR-ABM (SR-ABM) only applies when $LR(t)<1$ ($SR(t)<1$).

The ABM, $I^{h}(t)$ for $h=LR, SR$, adjusts both the notional rate g(t) and the pension indexation $\lambda (t)$ as follows:

$$\begin{aligned} 1+g^{h}(t)&=\left[ 1+g(t)\right] I^{h}(t)\end{aligned}$$

(3.15)

$$\begin{aligned} 1+\lambda ^{h}(t)&=\left[ 1+\lambda (t)\right] I^{h}(t) \end{aligned}$$

(3.16)

Following (Alonso-García et al., 2018), we define the symmetric ABMs in the following way.

• For $h=LR$, the symmetric LR-ABM is:

  $$\begin{aligned} I^{LR}(t)=\frac{C(t)+F^{LR-}(t)}{B^{LR}(t)},\end{aligned}$$

  where $F^{LR-}(t)$ and $B^{LR}(t)$ indicate respectively the reserve fund in the year t before contributions and benefit payments, and the amount of total pensions paid in the year t after the application of LR-ABM. The asymmetric LR-ABM is defined as:

  $$\begin{aligned}I^{LR}(t)=min\{LR(t);1\}.\end{aligned}$$

  The symmetric LR-ABM does not accumulate buffer funds.

• For $h=SR$, the symmetric SR-ABM is:

  $$\begin{aligned}I^{SR}(t)=\frac{CA^{SR}(t)+F^{SR-}(t)}{M^{SR}(t)+V^{SR}(t)},\end{aligned}$$

  where $CA^{SR}(t)$, $F^{SR-}(t)$, $M^{SR}(t)$ and $V^{SR}(t)$ are respectively the contribution assets, the reserve fund, the total notional amount and the total reserve for pensioners in the year t after the application of SR-ABM. The asymmetric SR-ABM is defined as:

  $$\begin{aligned}I^{SR}(t)=min\{SR(t);1\}.\end{aligned}$$

  The SR-ABM might accumulate buffer funds in both the symmetric and asymmetric cases.

4 Modeling macroeconomic variables and transition probabilities

To study the financial sustainability of an NDC pension system with LTC benefits, we have to forecast the evolution of the transition probabilities and the macroeconomic variables relevant to the system. As explained above, the pension indexation rate can be set equal at either the wage growth rate or the inflation rate. Since the numerical application is based on the Italian pension system, in which pensions are indexed to inflation, in the following, we illustrate how we model the evolution of the inflation rate and the wage growth rate. The development of a refined forecasting model for these variables is beyond the scope of this paper, which is to measure the NDC pension system’s evolution based on realistic assumptions of the economic and demographic scenarios. Therefore, in the following, we adopt some simplifying assumptions.

We model the transition probabilities through stochastic mortality models, the wage growth rate $\xi (t)$ and the inflation rate i(t) as stochastic processes. Therefore, we take into account both demographic and economic risks. The historical data stops in 2019 and refers to the period immediately preceding the COVID-19 crisis in order to disregard the effects of the pandemic that may produce anomalies in the results. The picture offered by our analysis should be contextualized at that time, with consequences also on inflation which was decidedly lower at the time, with expectations of much lower future levels than today. Finally, we assume independence between demographic and economic variables. We provide further details on the model selection process in the following.

4.1 Macroeconomic variables

The economic data consist of annual observations over the period 1983–2019 taken from the Italian National Institute of Statistics (ISTAT). Specifically, $\xi (t)$, derives from the wage growth rate for the period 1983–2015 and the gross contractual hourly remuneration of employees for the last four years. The inflation rate, i(t), is taken from the consumer price index for blue and white-collar worker households (FOI) for the period 1983–2019.

We use Vector Auto-Regressive (VAR) and Vector Error Correction Model (VECM) to represent the inflation rate and wage growth rate, and a mean-reversion to an exogenous long-run trend to obtain realistic projections (see (Lee & Tuljapurkar, 1998) for further details on this approach). The stationarity of macroeconomic variables is verified by two statistical tests, the Phillips-Perron (PP) and the Kwiatkowski-Phillips-Schmidt-Shin (KPSS) test, both at a 5% significance level. The wage growth rate and inflation rate show a stationary behaviour, which leads to excluding the VECM. We also carry out the Granger causality test at a 10% level. We find the VAR optimal number of parameters and check the model’s goodness of fit using the Akaike Information Criterion (AIC), the Hannan-Quinn information criterion (HQ), the Schwarz Information Criterion (SIC), and the Final Prediction Error (FPE).

Our results show that the VAR(1) is the most suitable model for the inflation rate and wage growth rate, with an exogenous long-run trend of 3.5% for the wage growth rate and 2% for the inflation rate in line with the long-term values chosen by the Ministry of Finance for the long-term projections of the national pensions expenditure (Ragioneria Generale dello Stato, 2020). Therefore, the inflation rate and the wage growth rate considering the exogenous long-run trends $\tau _i$ and $\tau _\xi$ and respectively denoted as $\bar{i}(t)=i(t)-\tau _i$ and $\bar{\xi }(t)=\xi (t)-\tau _\xi$, are jointly modelled as:

$$\begin{aligned} \bar{i}(t)&=c_{\bar{i}}+\phi _{1} \cdot \bar{i}(t-1)+\phi _{2} \cdot \bar{\xi }(t-1)+e_{\bar{i}}(t)\end{aligned}$$

(4.1)

$$\begin{aligned} \bar{\xi }(t)&=c_{\bar{\xi }}+\theta _{1} \cdot \bar{i}(t-1)+\theta _{2} \cdot \bar{\xi }(t-1)+e_{\bar{\xi }}(t) \end{aligned}$$

(4.2)

where $\phi _{1}$, $\phi _{2}$, $\theta _{1}$ and $\theta _{2}$ are the parameters of the model, $c_{\bar{{i}}}$ and $c_{\bar{\xi }}$ are constants serving as the intercept of the model, $e_{\bar{i}}(t)$ and $e_{\bar{\xi }}(t)$ are zero-mean white noise processes.

Equation 4.1 implies that the inflation rate in a certain year is related not only to the previous inflation rate (through parameter $\phi _1$) but also to the previous wage growth rate (through parameter $\phi _2$). A similar consideration can be made for the wage growth rate in Eq. 4.2.

4.2 Transition probabilities

For the transition probabilities of the model, we assume:

• $p^{12}(x,t)$ equal to 1 for $x=x_{r-1}$ and zero otherwise (we consider only one retirement age, supposed constant over time),

• $p^{13}(x,t)=0$ $\forall x,t$ (disability is considered only after retirement),

• $p^{14}(x,t)=0$ $\forall x,t$ (we disregard the mortality of contributors).

• $p^{21}(x,t)=0$ $\forall x,t$ (it is impossible to start working again after retirement).

• $p^{32}(x,t)=0$ $\forall x,t$ (we disregard the possibility of recovery from disability pensioner to healthy pensioner).

For the modeling of $p^{23}(x,t)$, $p^{24}(x,t)$ and $p^{34}(x,t)$, we refer to (Levantesi & Menzietti, 2018). Thus, these probabilities are modelled by the CBD model including an age-dependent cohort effect (CBD-8 model):

$$\begin{aligned} logit(p^{ij}_{x,t})= ln\left( \frac{p^{ij}_{x,t}}{1-p^{ij}_{x,t}}\right) = {^{ij}k_t^{(1)}}+{^{ij}k_t^{(2)}} (x-\bar{x})+ {^{ij}\gamma ^{(3)}_c (x_c-x)}\, , \end{aligned}$$

(4.3)

where x is the age, $\bar{x}$ the mean age in the sample age range, t the time, $c=t-x$ the cohort and $x_c$ a constant parameter that does not vary with age or time. The model is subject to the constraint $\sum _{c} ^{ij}\gamma _c^{(3)}=0$. The model’s parameters are estimated separately for each transition probability according to a trivariate CBD model.

The transition probabilities are fitted on the INPS (the Italian National Institute of Social Security) data on people qualified to the "indennita’ di accompagnamento".⁷ The dataset provides the number of deaths among the disabled, the number of disabled, and inceptions of the disabled state.

5 Numerical application

This section illustrates a numerical application of the model developed in Sects. 2 and 3, which introduces LTC benefits in the Italian NDC pension system and proposes two ABM used to restore the equilibrium of the system when financial sustainability issues arise. We build three scenarios. The base one considers a standard NDC pension system, without LTC benefits. The second and third ones refer to an NDC system with an EPA and LCA benefit, respectively. Then, for each scenario, we apply the symmetric ABM based on liquidity ratio (LR-ABM) or the ABM based on solvency ratio (SR-ABM) to investigate their effects on the financial sustainability and social adequacy of the Italian NDC pension system.

We assume an initial active population $N^1(0)=1,000$. The initial number of pensioners assumed all active in $t=0$, is obtained from the dependency ratio of the INPS pension fund for employees ("Fondo Pensioni Lavoratori Dipendenti" (FPLD)) in 2019, $D(0)=0.43$. Therefore $N^2(0)=430$ and $N^3(0)=0$. The initial age distributions for both active and pensioners and the initial distributions of wages and pension benefits are taken from the observed distributions of the FPLD in 2019. The retirement age, $x_r$, is set at 63 years, in line with the average retirement age of the FPLD in 2019. The contribution rate is set at 0.3,⁸ while we assume $\eta = 0.6$.

According to the features of the Italian NDC system, the notional rate, g(t), is set equal to the 5-years moving average of the GDP growth rate, and the pension indexation rate, $\lambda (t)$, is equal to the inflation rate i(t). We assume that the GDP growth rate is equal to the sum of the growth rate of the active population and the growth rate of the individual wage. We assume that the active population is constant over time, therefore, $\rho (t)=0$ $\forall t$. In the actuarial valuation, we adopt a constant discount rate j(t) equal to the long-run trend of real GDP growth rate, $j(t)=1.5\%$. Finally, we use a 75-year time horizon, compliant with the minimum value often considered in actuarial reports.

5.1 Results

The first step of the numerical application consists of projecting the future evolution of the Italian NDC system without LTC benefit (base scenario) and not introducing ABMs. The main results concerning the expected values of the dependency ratio D(t), the average pension b(t), the replacement rate r(t), and the equilibrium contribution rate $\hat{c}(t)$ are reported in Fig. 2, together with the 90% confidence intervals.

Fig. 2

Pension system evolution under the base scenario (without LTC benefits—no ABMs): Dependency ratio (a), Average pension (net of inflation) (b), Replacement rate (c) and Equilibrium contribution rate (d). Expected values and 90% confidence intervals

First, we observe that the expected value of the dependency ratio, D(t), increases rapidly in the first 30 years and then stabilizes from 2054 around the value of 0.8 (see also Table 1). This result is a consequence of the longer life expectancy of the population, which has not been compensated by an increase in the retirement age. The width of the 90% confidence interval of D(t) highlights the demographic uncertainty present in the system⁹: from Table 1, the lower and upper limits for 2094 are 0.68 and 0.91, respectively (-18% and +11% compared to the expected value).

Table 1 Expected values and confidence intervals of the dependency ratio D(t)

The average pension b(t) shows a slight increase in the first 15 years, followed by a small decrease until 2064, finally, it quickly increases in the last 30 years. This dynamic is the consequence of the progressive replacement of the initial generations of pensioners by generations of new pensioners. The first cohorts of pensioners still receive benefits from the old and too generous DB system, while the next cohorts are from the DC system. As a consequence of the slow growth/decrease of the average pension until 2064 (Fig. 2 (b)), the expected replacement rate shows a sharp reduction from 74% to 39% (see also the first line in Table 2). In the following years, r(t) decreases slowly, reaching the value of 35% in 2094. The 90% confidence interval of r(t) in 2094 is (0.33/0.38), or -8%/+8% compared to the expected value.

For the equilibrium contribution rate $\hat{c}(t)$, we observe that it increases in the first 25 years, then decreases until 2074, and finally remains stable at a value (0.29) close to (but smaller than) the contribution rate of the system, as shown in Fig. 2 (d). $\hat{c}(t)$ is characterized by a high uncertainty: the lower and upper limits of its 90% confidence interval for 2094 are 0.24 and 0.33, respectively (-16% and +13% compared to the central value, see line 2 in Table 3).

In the second step of the numerical application, we consider two alternative scenarios: the first one refers to an NDC pension system that provides an EPA benefit, while the other to a system including an LCA benefit. The embedding of the LTC benefits in the system does not affect the dependency ratio nor the evolution of the wage, therefore we can focus on the replacement rate¹⁰ (see lines 3–6 in Table 2) and equilibrium contribution rate (see lines 3–6 in Table 3). Both EPA and LCA produce an increase in the replacement rate, which was expected in the LCA because the increased disability benefit is financed by an extra contribution, whereas it was not so easily predictable in the EPA scenario (Fig. 3 (a)). However, the r(t) increase detected in the EPA scenario is small and due to the increase in the number of disabled people (receiving a higher level of benefits) compared to healthy pensioners (receiving a lower pension) in the long term. The 90% confidence interval of the replacement rate in the LTC scenarios is slightly wider than in the base scenario (lines 1, 3, and 5 in Table 2).

Fig. 3

Replacement rate (a) and equilibrium contribution rate (b) under the three scenarios: Base (grey), EPA (red) and LCA (blue). Expected values and 90% confidence intervals

Table 2 Expected values and confidence intervals of the replacement rate r(t) under the three scenarios: Base, EPA and LCA. No ABM, LR-ABM and SR-ABM

At the same time, the introduction of LTC benefits leads to an increase (which is small) in the equilibrium contribution rate of the system (Table 3). In the EPA scenario, the increase of $\hat{c}(t)$ is slighter (+1%) compared to the LCA scenario. This could be explained by the same reason underlying the replacement rate increase: in the long term, the number of people with disabilities rises more than the number of healthy pensioners (Fig. 3b). It is noteworthy that without ABM the 90% confidence interval for $\hat{c}(t)$ in both the EPA and LCA scenarios is narrower than the one in the base scenario: 0.09 in Base scenario, 0.08 in the EPA scenario, and 0.07 in the LCA scenario, with a 11.1% and 22.2% reduction, respectively. In other words, including LTC benefits increases the cost of pensions but reduces their uncertainty, thus reducing risk exposure for taxpayers. This reduction can be interpreted as a measure of the natural hedging between longevity and disability risk: when an LTC benefit is added to the basic pension, the pension level is increased for disabled people, growing the immediate cost to the system. However, disabled people have a lower life expectancy, thus offsetting the higher cost of disability. We observe that the reduction in risk exposure is not high and far from achieving perfect risk offsetting. We, therefore, conclude that introducing LTC benefits into the system has the positive effect of producing a natural hedge, even if the resulting risk reduction is only partial.

Table 3 Expected values and confidence intervals of the equilibrium contribution rate $\hat{c}(t)$ under the three scenarios: base, EPA and LCA. No ABM, LR-ABM and SR-ABM

Although the introduction of LTC benefits leads to a partial reduction of the uncertainty of the system, the value of the reserve fund in 2094 highlights a financial sustainability issue (see Table 4, column 2). In all scenarios, we obtain negative expected values of F(T), showing that the system accumulates liabilities over time. More in detail, the expected liability value is more than twice the expected total wages in 2094: 2.15 in the base scenario, 2.39 in the EPA scenario, and 2.12 in the LCA scenario. The lower uncertainty of the pension system embedding LTC benefits is confirmed by the standard deviation of F(T) compared to the expected total wages in the same year: 1.54 in the base scenario, 1.26 in the EPA scenario, and 1.29 in the LCA scenario.

To face the financial sustainability issue, in the third step of the numerical application, we apply the ABMs introduced in Sect. 3. The expected values and 90% confidence intervals of the replacement rate and the equilibrium contribution rate in the three scenarios with ABMs are reported in lines 7–18 of Tables 2 and 3, respectively. The evolution of r(t) and $\hat{c}(t)$ in both the LTC scenarios with the ABMs is shown in Fig. 4. The trends are very similar in the two scenarios,¹¹ even if the final values are not the same (see Tables 2 and 3).

Fig. 4

Replacement rate in the EPA scenario (a) and the LCA scenario (b). Equilibrium contribution rate in the EPA scenario (c) and the LCA scenario (d). Expected values and 90% confidence intervals. Legend: without ABM (grey), LR-ABM (red) and SR-ABM (blue)

In the early years, both the LR-ABM and SR-ABM reduce the pension indexation rate and the notional rate aiming to lower the system’s imbalance. However, we can observe an important difference between these two ABMs. LR-ABM works to stabilize the equilibrium contribution rate over time (the liquidity ratio is linked to $\hat{c}(t)$), while SR-ABM aims at stabilizing the system’s solvency in the long term, thus $\hat{c}(t)$ has wider confidence intervals (see Fig. 4c, d). At the same time, LR-ABM produces a reduction in the replacement rate lower than SR-ABM, especially in the short term, but with greater uncertainty in the medium-long term (see Fig. 4a, b). The results show that the introduction of LR-ABM produces an immediate and stable effect on the equilibrium contribution rate but leads to greater uncertainty in the replacement rate, and thus for pensioners.

We measure the effect of the introduction of ABMs on the financial sustainability of the system through the reserve fund at the end of the time horizon T (see Table 4). To better appreciate the values in Table 4, consider that the expected value of total wages in 2094 is 392 million euros.

Table 4 Expected values and (90% confidence intervals) of F(T), for the three scenarios (Base, EPA, LCA), with and without ABMs (values expressed in million euros)

The results show that the ABMs reduce the liability of the pension scheme. However, in the case of LR-ABM, the reserve fund remains close to zero over time, while in the case of SR-ABM, a reserve fund accumulates to cope with the lack of contribution assets with respect to the obligations towards actives and pensioners.

6 Conclusions

In this paper, we introduce two types of LTC benefits within the NDC architecture of the Italian pension system, adding a new risk source deriving from disability risk. We follow a stochastic environment, which allows us to detect the projections’ uncertainty through the calculations of confidence intervals of the relevant variables. Our model considers an LTC benefit that enhances the retirement pension received in the healthy state when the retiree becomes disabled. We analyze two types of LTC annuities: LCA, where the LTC benefit is obtained by increasing the basic pension of a fixed percentage, and EPA, where the uplift is financed through a reduction of the pension received in the healthy state.

The results show that the inclusion of LTC benefits does not change the main pension system indicators, leaving the expected value of the contribution rate unchanged (EPA scenario) or slightly increasing it (LCA scenario), and not affecting the dependency ratio. However, the introduction of these benefits in the NDC system slightly increases the pensions’ amount and partially reduces the contribution rate uncertainty, and thus the riskiness of the system. The latter finding confirms the existence of a natural hedging effect when LTC benefits are combined with life annuities (Levantesi & Menzietti, 2018). However, risk reduction is only partial, and the ABM introduction remains necessary.

We find that our NDC system shows some issues already before the introduction of LTC (first of all, a fast-growing dependency ratio). These issues are essentially due to the continuous rise in the population life expectancy, jeopardizing the financial sustainability of the system and the adequacy of future pension benefits. The value of the reserve fund at the end of the time horizon indeed highlights a financial sustainability issue that can be faced by including ABMs in the system.

The problem of social adequacy of pension benefits must be stressed. The Italian pension system shows a dramatic reduction in the average replacement rate. In our projections, this phenomenon already occurs in the standard system and is only partially reduced by the introduction of LCA and, to a lesser extent, by the EPA. We have shown that this issue is due to the progressive replacement of the old pensions, still calculated with the old and generous DB system, by the new pensions, which are determined by the NDC system. However, this is an aspect that cannot be overlooked and resolved either by increasing the retirement age or by increasing the contribution rate (the latter change being in contrast with the DC nature of the system). In this paper, we have not taken these two changes into account in order to better highlight the effects of the introduction of LTC benefits in the pension benefit, leaving the other elements unchanged.

We analyze the effect of two ABMs, one based on liquidity ratio (LR-ABM) that aims at stabilizing the equilibrium contribution rate over time, and the other on solvency ratio (SR-ABM) that aims at stabilizing the system’s solvency in the long term. Our analysis shows that they differently affect the pension system: LR-ABM provides a lower reduction in the replacement rate compared to SR-ABM (especially in the short term) and an immediate and stable effect on the equilibrium contribution rate. However, it raises the replacement rate uncertainty in the medium-long term. SR-ABM accumulates a reserve fund, while LR-ABM does not. Both ABMs are effective, reducing the liabilities of the system and restoring the financial equilibrium.