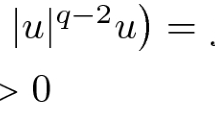Abstract
In this paper, we study a type of p-Laplacian equation
with prescribed mass
where \(1<p< q< p^{*}: = \frac{pN}{N-p}\), \(p < N\), \(\lambda \in {\mathbb {R}}\) is a Lagrange multiplier. Firstly, we prove the existence of normalized solutions to p-Laplacian equations and provide accurate descriptions; secondly, we discuss the existence of ground states; finally, we study the radial symmetry of normalized solutions in the mass supercritical case. Besides, we also study normalized solutions to p-Laplacian equation with a potential function V(x)
under different assumptions on q and the constraint norm c, we prove the existence, nonexistence, concentration phenomenon and exponential decay of normalized solutions.
Similar content being viewed by others
References
Agueh, M.: Sharp Gagliardo–Nirenberg inequalities via p-Laplacian type equations. Nonlinear Differ. Equ. Appl. NoDEA 15, 457–472 (2008)
Ambrosetti, A., Malchiodi, A.: Nonlinear Analysis and Semilinear Elliptic Problems, Cambridge Studies in Advanced Mathematics. Cambridge University Press, Cambridge (2007)
Bartsch, T., Soave, N.: A natural constraint approach to normalized solutions of nonlinear Schrödinger equations and systems. J. Func. Anal. 272, 4998–5037 (2017)
Bartsch, T., Soave, N.: Multiple normalized solutions for a competing system of Schrödinger equations. Cala. Var. Partial Differ. Equ. 58, 24 (2019)
Bartsch, T., Wang, Z.: Existence and multiplicity results for some superlinear elliptic problems on \({\mathbb{R} }^{N}\), Commun. Part. Differ. Equ. 20, 1725–1741 (1995)
Bellazzini, J., Siciliano, G.: Scaling properties of functionals and existence of constrained minimizers. J. Func. Anal. 261, 2486–2507 (2011)
Brézis, H.: Functional Analysis, Sobolev Spaces and Partial Differential Equations. Springer, New York (2011)
Chen, Y., Levine, S., Rao, M.: Linear Growth Functionals in Image Restoration. SIAM J. Appl. Math. 66, 1383–1406 (2006)
Damascelli, L., Pacella, F., Ramaswamy, M.: Symmetry of ground states of p-Laplace equations via the moving plane method. Arch. Rational Mech. Anal. 148, 292–308 (1999)
Demengel, F., Hebey, E.: On some nonlinear equations involving the \(p\)-Laplacian with critical Sobolev grough. Adv. Differ. Equ. 4, 533–574 (1998)
Du, M., Tian, L., Wang, J.: Existence of normalized solutions for nonlinear fractional Schrödinger equations with trapping potentials. Proc. R. Soc. Edinb. Sect. A 149, 617–653 (2019)
Ghoussoub, N.: Duality and Perturbation Methods in Critical Point Theory, Cambridge Tracts in Mathematics, vol. 107. Cambridge University Press, Cambridge (1993)
Gou, T., Zhang, Z.: Normalized solutions to the Chern–Simons–Schrödinger system. J. Func. Anal. 280, 108894 (2021)
Gu, L., Zeng, X., Zhou, H.: Eigenvalue problem for a p-Laplacian equation with trapping potential. Nonlinear Anal. 148, 212–227 (2017)
Guo, Y., Seiringer, R.: On the mass concentration for Bose–Einstein condensates with attractive interactions. Lett. Math. Phys. 104, 141–156 (2014)
Guo, Y., Zeng, X., Zhou, H.: Energy estimates and symmetry breaking in attractive Bose–Einstein condensates with ring-sharped potential. Ann. Inst. Henri Poincaré Non Linéaire 33, 809–828 (2016)
Jeanjean, L., Luo, T.: Sharp nonexistence results of prescribed \(L^{2}\)-norm solutions for some class of Schrödinger–Poisson and quasi-linear equations. Z. Angew. Math. Phys. 64, 937–954 (2013)
Jeanjean, L., Luo, T., Wang, Z.: Multiple normalized solutions for quasi-linear Schrödinger equations. J. Differ. Equ. 259, 3894–3928 (2015)
Li, G., Ye, H.: On the concentration phenomenon of \(L^{2}\)-subcritical constrained minimizers for a class of Kirchhoff equations with potentials. J. Differ. Equ. 266, 7101–7123 (2019)
Lions, P.: The concentration-compactness principle in the calculus of variations, The locally compact case I. Ann. Inst. Henri Poincaré, Non Linéaire 1, 109–145 (1984)
Lou, Q., Mao, A., You, J.: Standing waves for a class of fractional p-Laplacian equations with a general critical nonlinearity. Math. Meth. Appi. Sci. 44, 960–984 (2021)
Lou, Q., Qin, Y., Liu, F.: The existence of constrained minimizers related to fractional \(p\)-Laplacian equations. Topol. Methods Nonlinear Anal. 58, 657–676 (2021)
Luo, H., Zhang, Z.: Normalized solutions to the fractional Schrödinger equations with combined nonlinearities. Cala. Var. Partial Differ. Equ. 59, 35 (2020)
Mastorakis, N., Fathabadi, H.: On the solution of p-Laplacian for non-newtonian fluid flow. WSEAS Trans. Math. 8, 238–245 (2009)
Oden, J.: Existence theorems and approximations in nonlinear elasticity. In: Lakshmi-Kantham, E. (ed.) NonIinear Equations in Abstract Spaces. North-Holland, Amsterdam (1978)
Pelissier, M.: SurqueIques problemes non-lineaires en glaciologie, These, Pub1. Math. d’Orsay, 110 (1975)
Pucci, P., Serrin, J.: A general variational identity. Indiana Univ. Math. J. 35, 681–703 (1986)
Qin, Y., Wang, Z., Zou, L.: Analytical solutions and dynamic behaviors to synchronous oscillation of same bubbles at vertices of cuboid and rectangle. Phys. Fluids 35, 082004 (2023)
Rabinowitz, P.: Minimax Methods in Critical Point Theory with Applications to Differential Equations, CBMS Regional Conference Series in Mathematics, vol. 65. American Mathematical Society, Providence (1986)
Schoemaver, M.: A monodimensional model for fracturing. In: Fasano, A., Primicerio, M. (eds.) Free Boundary Problems: Theory and Applications. Research Notes in Mathemetics, vol. 79, pp. 701–711. Pitman, London (1983)
Serrin, J., Tang, M.: Uniqueness of ground states for quasilinear elliptic equations. Indiana Univ. Math. J. 49, 897–923 (2000)
Soave, N.: Normalized ground states for the NLS equation with combined nonlinearities. J. Differ. Equ. 269, 6941–6987 (2020)
Soave, N.: Normalized ground states for the NLS equation with combined nonlinearities: the critical case. J. Func. Anal. 279, 108610 (2020)
Uhlenbeck, K.: Regularity for a class of nonlinear elliptic systems. Acta Math. 138, 219–240 (1977)
Volker, R.: Nonlinear flow in porous media by finite elements. J. Hydraul. Div. Proc. Am. Sc. Civ. Eng. 95, 2093–2113 (1969)
Weinstein, M.: Nonlinear Schrödinger equations and sharp interpolation estimates. Commun. Math. Phys. 87, 567–576 (1983)
Zhang, Z.: Variational, Topological, and Partial Order Methods with Their Applications. Springer, New York (2013)
Zhang, Z., Zhang, Z.: Normalized solutions to p-laplacian equations with combined nonlinearities. Nonlinearity 35, 5621–5663 (2022)
Acknowledgements
The authors are grateful to the reviewers for their helpful comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Zhang is supported by National Key R &D Program of China(2022YFA1005601) and NSFC(12031015), Q. Lou is supported by NSFC(12001233), Shandong Province Natural Sciences Fund(ZR2020QA007) and China Postdoctoral Science Fund(2022M711928).
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Lou, Q., Zhang, Z. Multiplicity and concentration of normalized solutions to p-Laplacian equations. Z. Angew. Math. Phys. 75, 81 (2024). https://doi.org/10.1007/s00033-024-02219-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00033-024-02219-6