1 Introduction

Fractional order differential equations are a significant concept as an extension of integer order differential equations because they provide a better explanation of physical processes than traditional derivatives. Consequently, fractional differential equations are frequently utilized and researched as the best way to model technical and physical processes. In recent years, nonlinear fractional partial differential (NFPDEs) have been used to model many physical phenomena in various fields, such as fluid mechanics, solid-state physics, plasma physics, chemical physics, fiber optics, and geochemistry. For fractional differential equations, there are some derivative definitions. They include Riemann–Liouville, Caputo, and conformable fractional derivatives. Today, many people employ the Riemann-Liouville fractional derivative method. It combines two well-known mathematicians, Riemann and Liouville, fractional derivative procedures. Furthermore, scientists commonly employ Caputo derivatives. The conformable derivative [1, 2] is also documented in addition to these derivatives. It satisfies the chain rule, which makes it possible to find reliable exact solutions for fractional differential equations, in contrast to the Caputo and Riemann-Liouville definitions. Great progress has been made in finding exact solutions to nonlinear equations, but these advances have not been sufficient. As a result, analytical approaches have been used, and it has been discovered that there is no one method that can be used to provide exact solutions to nonlinear problems of every kind. Consequently, numerous techniques have been developed, including \((G'/G)\)-expansion method and its modification [3, 4], sub-equation method [5], simple equation method and its modification [6,7,8], modified Kudryashov method [9], sine-cosine method [10], tanh-coth expansion method [11], sinh-Gordon equation expansion method [12], Hirota method [13, 14], generalized Riccati equation mapping method [15], homotopy analysis method [16], new version of trial equation method [17], improved Bernoulli sub-equation function method [18], exp(-\(\varphi (\xi \)))-expansion method [19,20,21], unified method [22, 23], first integral method [24], Sardar sub-equation method [25, 26], etc.

Although these methods can yield exact solutions for specific kinds of equations, they come with several drawbacks and limitations. Analytical techniques are frequently restricted to particular partial differential equations (PDEs) classes with established solutions. Real-world PDEs can be highly complex and nonlinear. In many circumstances, it is mathematically difficult or impossible to obtain analytical solutions for such equations. Solving some PDEs analytically can be computationally difficult since they need complex mathematical computations. This may reduce the viability of using these techniques for more complicated problems. Additionally, analytical approaches become more difficult when the problem’s dimensionality rises. Although many methods are effective in one or two dimensions, applying them in three or more dimensions may be challenging. The balancing principle and determining an N value are the starting points for both of the two approaches that have been suggested in this study. Nevertheless, the methods will not function with equations that have non-integer balancing values. Furthermore, these approaches may not be fully applicable when dealing with some higher-order PDEs. As a result, these methods are case-specific and work well for some PDEs but need to be better for others.

Many physicists and mathematicians have proposed various mathematical models to understand the state of water waves that occur in shallow water regimes. Two Dutch mathematicians, D. J. Korteweg and G. de Vries, worked on this mathematical theory and obtained a nonlinear partial differential equation that models the motion of two-dimensional, unidirectional propagating water waves on the free surface of a shallow layer of water. Thus, the Korteweg–de Vries (KdV) equation emerges as a mathematical model [27]. By developing this equation, some exemplary equations are also created, some of which are the modified KdV (mKdV) equation [28], Korteweg–de Vries–Burgers (KdV-B) equation [29], modified Korteweg–de Vries Zakharov–Kuznetsov (mKdv-ZK) equation [30], Korteweg–de Vries Benjamin–Bona–Mahony equation [31], etc.

In this study, we consider the following (3+1)-dimensional KdV-BBM equation

$$\begin{aligned} u_{xt}+\mu _{1}(uu_{x})_{x}+\mu _{2}u_{xxxx}-\mu _{3}u_{xxxt}+\mu _{4}u_{yy}-\mu _{5}u_{zz}=0. \end{aligned}$$
(1)

The study of wave propagation in many physical systems, especially fluid dynamics and nonlinear optics, gives rise to the Korteweg–de Vries Benjamin–Bona–Mahony (KdV-BBM) equation. Features from the Benjamin–Bona–Mahony (BBM) equation and the Korteweg–de Vries (KdV) equation are combined in this equation. This equation addresses the evolution of specific types of waves, such as solitary waves, in dispersive media and multidimensional systems. In the study of water waves, the KdV-BBM equation appears as a model for the evolution of surface waves, especially in shallow water where nonlinear effects become substantial. In a dispersive medium, it characterizes the behavior of long, nonlinear waves with small amplitude, allowing for both dispersion and dissipation effects.

There exist some studies about the model in the literature. Soliton solutions of the model are presented by the auxiliary equation method in [30]. Invariant analysis and conservation laws of the model are given by Lie symmetry method in [32]. Multiple rogue wave solutions to the model were obtained by a symbolic calculation approach in [33]. Multi-soliton solutions of the model are derived by the modified hyperbolic function expansion method [34]. Finally, rogue wave solutions of the model are provided by the Hirota’s bilinear method [35].

To the authors’ knowledge, the fractional version of the model has not been studied yet. Therefore, as an extension of the above work, we obtained the exact solutions of this equation, which we created by using the conformable fractional derivative, the modified generalized Kudryashov, and exp(-\(\varphi (\xi \)))-expansion methods. After that, the graphs were produced by giving appropriate values to the exact solutions we had discovered.

The following is how the paper is organized. The fundamental definitions go in Sect. 2. In Sects. 3 and  4, the generalized modified Kudryashov and exp(-\(\varphi (\xi \)))-expansion approaches are presented respectively. In Sect. 5, the governing equation’s solutions are provided. In the rest, graphical representations, sensitivity analysis, and concluded remarks are listed.

2 Preliminaries

Definition 1

The conformable derivative of a \(g:[0,\infty )\rightarrow \mathbb {R}\) function of order \(\omega \) for \(t>0\) and \(\omega \in (0,1)\) is defined as [1],

$$\begin{aligned} \mathscr {D}_{t}^{\omega }(g)(t)=\lim _{\beta \rightarrow 0}\frac{g(t+\beta t^{1-\omega })-g(t)}{\beta }. \end{aligned}$$
(2)

Furthermore, if g is \(\omega \)-differentiable in range (0, k), for \(k>0\) and the \(\lim _{t\rightarrow 0^{+}}{\mathscr {D}_{t}^{\omega }(g)(t)}\) exists, then definition writes

$$\begin{aligned} \mathscr {D}_{t}^{\omega }(g)(0)=\lim _{t\rightarrow 0^{+}}{\mathscr {D}_{t}^{\omega }(g)(t)}. \end{aligned}$$
(3)

Lemma 1

Let \(g_{1}\) and \(g_{2}\) be \(\omega \)-differentiable at \(t>0\), for \(0<\omega \le 1\). Then [1, 36],

  1. i.

    \(\mathscr {D}_{t}^{\omega }(t^{h_{1}})=h_{1}t^{h_{1}-\omega },\,h_{1}\in \mathbb {R}\),

  2. ii.

    \(\mathscr {D}_{t}^{\omega }(h_{1}g_{1}+h_{1}g_{2})=h_{1}\mathscr {D}_{t}^{\omega }(g_{1})+h_{2}\mathscr {D}_{t}^{\omega }(g_{2}),\,h_{1},h_{2}\in \mathbb {R}\),

  3. iii.

    \(\mathscr {D}_{t}^{\omega }\left( \frac{h_{1}}{h_{2}}\right) =\frac{h_{2}.\mathscr {D}_{t}^{\omega }(h_{1})-h_{1}.\mathscr {D}_{t}^{\omega }(h_{2})}{h_{2}^2}\),

  4. iv.

    \(\mathscr {D}_{t}^{\omega }(h_{1}.h_{2})=h_{1}.\mathscr {D}_{t}^{\omega }(h_{2})+h_{2}.\mathscr {D}_{t}^{\omega }(h_{1})\),

  5. v.

    \(\mathscr {D}_{t}^{\omega }(g_{1})(t)=t^{1-\omega }\frac{dg_{1}(t)}{dt}\),

  6. vi.

    \(\mathscr {D}_{t}^{\omega }(C)=0\), if C=const.

3 The modified generalized Kudryashov method

The generalized modified Kudryashov approach is presented in this section, which consists of four main steps [37].

Step 1: We suppose general form of the nonlinear fractional partial differential equation of the type

$$\begin{aligned} \mathscr {P}(u,\mathscr {D}_t^{\omega },\mathscr {D}_x u,\mathscr {D}_y u,\mathscr {D}_x^2 u,\mathscr {D}_y^2 u,...)=0, \end{aligned}$$
(4)

where the conformable derivative is denoted by \(\mathscr {D}_t^{\omega }\).

Step 2: Applying the following travelling wave transform to Eq. (4)

$$\begin{aligned} u(x,...,t)=u(\xi ),\ \ \xi =kx+...+c\frac{t^\omega }{\omega }, \end{aligned}$$
(5)

where k and c are constants, the equation reduces to a nonlinear ordinary differential equation

$$\begin{aligned} \Omega (u(\xi ),u'(\xi ),u''(\xi ),...)=0. \end{aligned}$$
(6)

When \(\Omega \) is a polynomial in \(u(\xi )\), the superscripts represent the regular derivatives of \(u(\xi )\) with regard to \(\xi \). Eq. (6) is then integrated as long as all terms contain derivatives where integration constants are considered as zeros.

Step 3: Let take into account the solution of the Eq. (6) in the following form

$$\begin{aligned} u(\xi )=\sum _{m=0}^{N} \frac{a_m}{\left( 1+ Q (\xi )\right) ^{m} }, \end{aligned}$$
(7)

where \( a_m, \left( m=0,1,...,N\right) \) is an unknown constant. Moreover \(Q(\xi )\) will satisfy the following Riccati equation:

$$\begin{aligned} Q'(\xi )={\alpha + \beta Q(\xi )+\gamma Q(\xi )^2}, \end{aligned}$$
(8)

where \(\alpha , \beta , \gamma \) are real constants. The solutions of Eq. (8) for different cases of these coefficients are as follows:

  • When \(\alpha \), \(\beta \) are arbitrary constants and \(\gamma \ne 0\), then \(Q(\xi )\) can be expressed as

    $$\begin{aligned} Q(\xi )=\frac{\sqrt{4 \alpha \gamma -\beta ^2} \tan \left( \frac{1}{2} (d+\xi ) \sqrt{4 \alpha \gamma -\beta ^2}\right) -\beta }{2 \gamma }. \end{aligned}$$
    (9)

  • When \(\alpha =0\), \(\beta \ne 0 \), and \(\gamma \) is arbitrary constant, then \(Q(\xi )\) can be written as

    $$\begin{aligned} Q(\xi )=-\frac{\beta e^{\beta (d+\xi )}}{\gamma e^{\beta (d+\xi )}-1}. \end{aligned}$$
    (10)

  • When \(\alpha \) is arbitrary constant, \(\beta \ne 0 \), and \(\gamma =0\), then \(Q(\xi )\) be given by,

    $$\begin{aligned} Q(\xi )=-\frac{\alpha }{\beta }+\frac{e^{\beta (d+\xi )}}{\beta }. \end{aligned}$$
    (11)

Step 4: Applying the balancing rule to Eq. (6) will provide the balancing constant \(N\in \mathbb {Z^{+}}\). Putting Eq. (7) along with Eqs. (9),(10), (11), respectively, into Eq. (6) and equating the coefficients of powers of \(Q^{i}(\xi )\) \(m=0,1,2...\) equal to zero, we get a system of algebraic equations in parameters \(a_{m},\left( m=0.1,...,N\right) , k,\) and c. Substituting the resulting \(a_{m},\left( m=0.1,...,N\right) , k,\) and c into (7) gives the analytical solution to (6).

4 The exp\((-\varphi (\xi ))\)-expansion method

The subsequent stages should be used in a manner similar to how the initial two steps in the previous technique were carried out.

Step 1: As a finite series, exact solutions can be constructed as

$$\begin{aligned} u(\xi )=\sum _{r=0}^{N}B_r(exp(-\varphi (\xi )))^{r},\ \ B_N\ne 0, \end{aligned}$$
(12)

where the following ordinary differential equation is satisfied by \(\varphi =\varphi (\xi )\).

$$\begin{aligned} \varphi '(\xi )=exp(-\varphi (\xi ))+\eta exp(\varphi (\xi ))+\lambda . \end{aligned}$$
(13)

Step 2: Eq. (13) yields the following solutions depending on the relevant parameters, where an integration constant, h, is present.

When \(\eta \ne 0\), and \(\lambda ^2-4\eta >0\),

$$\begin{aligned} \varphi _{1}(\xi )=\ln \left( \frac{-\sqrt{(\lambda ^2-4\eta )} \tanh \left( \frac{\sqrt{(\lambda ^2-4\eta )}}{2}(\xi +h)\right) -\lambda }{2\eta }\right) , \end{aligned}$$
(14)

when \(\eta \ne 0\), and \(\lambda ^2-4\eta <0\),

$$\begin{aligned} \varphi _2(\xi )=\ln \left( \frac{\sqrt{(4\eta -\lambda ^2)} \tan \left( \frac{\sqrt{(4\eta -\lambda ^2)}}{2}(\xi +h)\right) -\lambda }{2\eta }\right) , \end{aligned}$$
(15)

when \(\eta =0\), and \(\lambda ^2-4\eta >0\), \(\lambda \ne 0\),

$$\begin{aligned} \varphi _3(\xi )=-\ln \left( \frac{\lambda }{\sinh (\lambda (h+\xi ))+\cosh (\lambda (h+\xi ))-1}\right) , \end{aligned}$$
(16)

when \(\eta \ne 0\), \(\lambda \ne 0\), and \(\lambda ^2-4\eta =0\),

$$\begin{aligned} \varphi _4(\xi )=\ln \left( -\frac{2(\lambda (\xi +h)+2)}{\lambda ^2(\xi +h)}\right) , \end{aligned}$$
(17)

when \(\lambda =0\), \(\eta =0\), and \(\lambda ^2-4\eta =0\),

$$\begin{aligned} \varphi _5(\xi )=\ln (\xi +h). \end{aligned}$$
(18)

Step 3: The final step of the preceding technique is also used to arrive at the equation’s solutions.

5 Solutions for (3+1)-dimensional KdV-BBM equation

Take into account the fractional form of Eq. (1)

$$\begin{aligned} \mathscr {D}_t^{\omega }u_{x}+\mu _{1}(uu_{x})_{x}+\mu _{2}u_{xxxx}-\mu _{3}\mathscr {D}_t^{\omega }u_{xxx}+\mu _{4}u_{yy}-\mu _{5}u_{zz}=0. \end{aligned}$$
(19)

We obtain the following equation by using the transformations in Eq. (5), and integrating twice,

$$\begin{aligned} -c k^3 \mu _3 u''+c k u+k^4 \mu _2 u''+\frac{1}{2} k^2 \mu _1 u^2-\mu _5 s^2 u+\mu _4 u w^2=0. \end{aligned}$$
(20)

5.1 Analytical solutions for (3+1)-dimensional KdV-BBM equation via the modified generalized Kudryashov method

The balance between \(u''\) and \(u^2\) gives \(N=2\). Thus, the predicted solution (7) takes the form

$$\begin{aligned} u(\xi )=a_0+\frac{a_1}{1+ Q(\xi ) }+\frac{a_2}{(1+Q(\xi ))^2}, \end{aligned}$$
(21)

and when paired with Eq. (8), the following system arises.

$$\begin{aligned}{} & {} -4 \alpha ^2 a_1 c k^3 \mu _3-12 \alpha ^2 a_2 c k^3 \mu _3+2 \alpha a_1 \beta c k^3 \mu _3+4 \alpha a_2 \beta c k^3 \mu _3+2 a_0 c k+2 a_1 c k+2 a_2 c k+4 \alpha ^2 a_1 k^4 \mu _2 \nonumber \\{} & {} \quad +12 \alpha ^2 a_2 k^4 \mu _2-2 \alpha a_1 \beta k^4 \mu _2-4 \alpha a_2 \beta k^4 \mu _2+a_0^2 k^2 \mu _1+a_1^2 k^2 \mu _1+a_2^2 k^2 \mu _1+2 a_0 a_1 k^2 \mu _1+2 a_0 a_2 k^2 \mu _1 \nonumber \\{} & {} \quad +2 a_1 a_2 k^2 \mu _1-2 a_0 \mu _5 s^2-2 a_1 \mu _5 s^2-2 a_2 \mu _5 s^2+2 a_0 \mu _4 w^2+2 a_1 \mu _4 w^2+2 a_2 \mu _4 w^2=0, \nonumber \\{} & {} \quad -4 \alpha ^2 a_1 c k^3 \mu _3-4 \alpha a_1 \beta c k^3 \mu _3-20 \alpha a_2 \beta c k^3 \mu _3+4 \alpha a_1 c \gamma k^3 \mu _3+8 \alpha a_2 c \gamma k^3 \mu _3+2 a_1 \beta ^2 c k^3 \mu _3 \nonumber \\{} & {} \quad +4 a_2 \beta ^2 c k^3 \mu _3+ 8 a_0 c k+6 a_1 c k+4 a_2 c k+4 \alpha ^2 a_1 k^4 \mu _2+4 \alpha a_1 \beta k^4 \mu _2+20 \alpha a_2 \beta k^4 \mu _2-4 \alpha a_1 \gamma k^4 \mu _2 \nonumber \\{} & {} \quad -8 \alpha a_2 \gamma k^4 \mu _2-2 a_1 \beta ^2 k^4 \mu _2-4 a_2 \beta ^2 k^4 \mu _2+4 a_0^2 k^2 \mu _1+2 a_1^2 k^2 \mu _1+6 a_0 a_1 k^2 \mu _1+4 a_0 a_2 k^2 \mu _1\nonumber \\{} & {} \quad +2 a_1 a_2 k^2 \mu _1-8 a_0 \mu _5 s^2-6 a_1 \mu _5 s^2-4 a_2 \mu _5 s^2+8 a_0 \mu _4 w^2+6 a_1 \mu _4 w^2+4 a_2 \mu _4 w^2=0,\nonumber \\{} & {} \quad -6 \alpha a_1 \beta c k^3 \mu _3-16 \alpha a_2 c \gamma k^3 \mu _3-8 a_2 \beta ^2 c k^3 \mu _3+6 a_1 \beta c \gamma k^3 \mu _3+12 a_2 \beta c \gamma k^3 \mu _3+12 a_0 c k+6 a_1 c k \nonumber \\{} & {} \quad +2 a_2 c k+6 \alpha a_1 \beta k^4 \mu _2+16 \alpha a_2 \gamma k^4 \mu _2+8 a_2 \beta ^2 k^4 \mu _2-6 a_1 \beta \gamma k^4 \mu _2-12 a_2 \beta \gamma k^4 \mu _2+6 a_0^2 k^2 \mu _1 \nonumber \\{} & {} \quad +a_1^2 k^2 \mu _1+6 a_0 a_1 k^2 \mu _1+2 a_0 a_2 k^2 \mu _1-12 a_0 \mu _5 s^2-6 a_1 \mu _5 s^2-2 a_2 \mu _5 s^2+12 a_0 \mu _4 w^2+6 a_1 \mu _4 w^2 \nonumber \\{} & {} \quad +2 a_2 \mu _4 w^2=0,\nonumber \\{} & {} \quad -6 \alpha a_1 \beta c k^3 \mu _3-16 \alpha a_2 c \gamma k^3 \mu _3-8 a_2 \beta ^2 c k^3 \mu _3+6 a_1 \beta c \gamma k^3 \mu _3+12 a_2 \beta c \gamma k^3 \mu _3+12 a_0 c k+6 a_1 c k\nonumber \\{} & {} \quad +2 a_2 c k+6 \alpha a_1 \beta k^4 \mu _2+16 \alpha a_2 \gamma k^4 \mu _2+8 a_2 \beta ^2 k^4 \mu _2-6 a_1 \beta \gamma k^4 \mu _2-12 a_2 \beta \gamma k^4 \mu _2+6 a_0^2 k^2 \mu _1+ \mu _1\nonumber \\{} & {} \quad +a_1^2 k^2 \mu _1+6 a_0 a_1 k^2+ 2 a_0 a_2 k^2 \mu _1-12 a_0 \mu _5 s^2-6 a_1 \mu _5 s^2-2 a_2 \mu _5 s^2+12 a_0 \mu _4 w^2+6 a_1 \mu _4 w^2\nonumber \\{} & {} \quad +2 a_2 \mu _4 w^2=0,\nonumber \\{} & {} \quad -4 \alpha a_1 c \gamma k^3 \mu _3-2 a_1 \beta ^2 c k^3 \mu _3+4 a_1 \beta c \gamma k^3 \mu _3-12 a_2 \beta c \gamma k^3 \mu _3+4 a_1 c \gamma ^2 k^3 \mu _3+8 a_2 c \gamma ^2 k^3 \mu _3+8 a_0 c k\nonumber \\{} & {} \quad +2 a_1 c k4 \alpha a_1 \gamma k^4 \mu _2+2 a_1 \beta ^2 k^4 \mu _2-4 a_1 \beta \gamma k^4 \mu _2+12 a_2 \beta \gamma k^4 \mu _2-4 a_1 \gamma ^2 k^4 \mu _2-8 a_2 \gamma ^2 k^4 \mu _2\nonumber \\{} & {} \quad +4 a_0^2 k^2 \mu _1+2 a_0 a_1 k^2 \mu _1-8 a_0 \mu _5 s^2-2 a_1 \mu _5 s^2+8 a_0 \mu _4 w^2+2 a_1 \mu _4 w^2=0, \nonumber \\{} & {} \quad -2 a_1 \beta c \gamma k^3 \mu _3+4 a_1 c \gamma ^2 k^3 \mu _3-4 a_2 c \gamma ^2 k^3 \mu _3+2 a_0 c k+2 a_1 \beta \gamma k^4 \mu _2-4 a_1 \gamma ^2 k^4 \mu _2+4 a_2 \gamma ^2 k^4 \mu _2 \nonumber \\{} & {} \quad +a_0^2 k^2 \mu _1-2 a_0 \mu _5 s^2+2 a_0 \mu _4 w^2=0. \end{aligned}$$

Solving the system above yields the following two cases and sets of solutions.

Case 1.

$$\begin{aligned} a_0= & {} \frac{12 \gamma (\alpha -\beta +\gamma ) \left( k^2 \mu _2+\mu _3 \left( \mu _4 w^2-\mu _5 s^2\right) \right) }{\mu _1 \left( k^2 \mu _3 \left( \beta ^2-4 \alpha \gamma \right) -1\right) }; \quad a_1=\frac{12 (\beta -2 \gamma ) (\alpha -\beta +\gamma ) \left( k^2 \mu _2+\mu _3 \left( \mu _4 w^2-\mu _5 s^2\right) \right) }{\mu _1 \left( k^2 \mu _3 \left( \beta ^2-4 \alpha \gamma \right) -1\right) };\nonumber \\ a_2= & {} \frac{12 (\alpha -\beta +\gamma )^2 \left( k^2 \mu _2+\mu _3 \left( \mu _4 w^2-\mu _5 s^2\right) \right) }{\mu _1 \left( k^2 \mu _3 \left( \beta ^2-4 \alpha \gamma \right) -1\right) }; \quad c=\frac{k^4 \mu _2 \left( \beta ^2-4 \alpha \gamma \right) -\mu _5 s^2+\mu _4 w^2}{k^3 \mu _3 \left( \beta ^2-4 \alpha \gamma \right) -k}, \end{aligned}$$
(22)

where \( \omega ,k, s, \mu _1, \mu _2, \mu _3, \mu _4, \mu _5 \) are arbitrary constants.

Set 1.1. Substituting (22) into the Eq. (9) gives the following solution:

$$\begin{aligned} u_{1.1}= & {} -\frac{12 \gamma (\alpha -\beta +\gamma ) \left( 4 \alpha \gamma -\beta ^2\right) \left( k^2 \mu _2+\mu _3 \left( \mu _4 w^2-\mu _5 s^2\right) \right) }{\mu _1 \left( 1-k^2 \mu _3 \left( \beta ^2-4 \alpha \gamma \right) \right) } \times \nonumber \\{} & {} \times \frac{\sec ^2\left( \frac{\sqrt{4 \alpha \gamma -\beta ^2}}{2} \left( d+\frac{t^{\omega } \left( k^4 \mu _2 \left( \beta ^2-4 \alpha \gamma \right) -\mu _5 s^2+\mu _4 w^2\right) }{\omega \left( k^3 \mu _3 \left( \beta ^2-4 \alpha \gamma \right) -k\right) }+k x+s z+w y\right) \right) }{\left( \beta -2 \gamma -\sqrt{4 \alpha \gamma -\beta ^2} \tan \left( \frac{\sqrt{4 \alpha \gamma -\beta ^2}}{2} \left( d+\frac{t^{\omega } \left( k^4 \mu _2 \left( \beta ^2-4 \alpha \gamma \right) -\mu _5 s^2+\mu _4 w^2\right) }{\omega \left( k^3 \mu _3 \left( \beta ^2-4 \alpha \gamma \right) -k\right) }+k x+s z+w y\right) \right) \right) {}^2}.\nonumber \\ \end{aligned}$$
(23)

Set 1.2. Substituting (22) into the Eq. (10) gives the following solution:

$$\begin{aligned} u_{1.2}= & {} -\frac{12 \beta ^2 (\beta -\gamma ) \left( k^2 \mu _2+\mu _3 \left( \mu _4 w^2-\mu _5 s^2\right) \right) }{\mu _1 \left( \beta ^2 k^2 \mu _3-1\right) } \times \nonumber \\{} & {} \quad \times \frac{ \exp \left( \beta \left( d+\frac{t^{\omega } \left( \beta ^2 k^4 \mu _2-\mu _5 s^2+\mu _4 w^2\right) }{\omega \left( \beta ^2 k^3 \mu _3-k\right) }+k x+s z+w y\right) \right) }{\left( (\beta -\gamma ) \exp \left( \beta \left( d+\frac{t^{\omega } \left( \beta ^2 k^4 \mu _2-\mu _5 s^2+\mu _4 w^2\right) }{\omega \left( \beta ^2 k^3 \mu _3-k\right) }+k x+s z+w y\right) \right) +1\right) {}^2}. \end{aligned}$$
(24)

Set 1.3. Substituting (22) into the Eq. (11) yields

$$\begin{aligned} u_{1.3}= & {} -\frac{12 \beta ^2 (\beta -\alpha ) \left( k^2 \mu _2+\mu _3 \left( \mu _4 w^2-\mu _5 s^2\right) \right) }{\mu _1 \left( \beta ^2 k^2 \mu _3-1\right) }\times \nonumber \\{} & {} \quad \times \frac{\exp \left( \beta \left( d+\frac{t^{\omega } \left( \beta ^2 k^4 \mu _2-\mu _5 s^2+\mu _4 w^2\right) }{\omega \left( \beta ^2 k^3 \mu _3-k\right) }+k x+s z+w y\right) \right) }{ \left( -\alpha +\beta +\exp \left( \beta \left( d+\frac{t^{\omega } \left( \beta ^2 k^4 \mu _2-\mu _5 s^2+\mu _4 w^2\right) }{\omega \left( \beta ^2 k^3 \mu _3-k\right) }+k x+s z+w y\right) \right) \right) {}^2}. \end{aligned}$$
(25)

Case 2.

$$\begin{aligned} a_0= & {} -\frac{2 \left( 2 \gamma (\alpha +3 \gamma )+\beta ^2-6 \beta \gamma \right) \left( k^2 \mu _2+\mu _3 \left( \mu _4 w^2-\mu _5 s^2\right) \right) }{\mu _1 \left( k^2 \mu _3 \left( \beta ^2-4 \alpha \gamma \right) +1\right) }; \nonumber \\ a_1= & {} -\frac{12 (\beta -2 \gamma ) (\alpha -\beta +\gamma ) \left( k^2 \mu _2+\mu _3 \left( \mu _4 w^2-\mu _5 s^2\right) \right) }{\mu _1 \left( k^2 \mu _3 \left( \beta ^2-4 \alpha \gamma \right) +1\right) };\nonumber \\ a_2= & {} -\frac{12 (\alpha -\beta +\gamma )^2 \left( k^2 \mu _2+\mu _3 \left( \mu _4 w^2-\mu _5 s^2\right) \right) }{\mu _1 \left( k^2 \mu _3 \left( \beta ^2-4 \alpha \gamma \right) +1\right) }; \nonumber \\ c= & {} \frac{k^4 \mu _2 \left( \beta ^2-4 \alpha \gamma \right) +\mu _5 s^2-\mu _4 w^2}{k^3 \mu _3 \left( \beta ^2-4 \alpha \gamma \right) +k}, \end{aligned}$$
(26)

where \( \omega ,k, s, \mu _1, \mu _2, \mu _3, \mu _4, \mu _5 \) are arbitrary constants.

Set 2.1. Substituting Eq. (26) into Eq. (9), gives

$$\begin{aligned}{} & {} u_{1.4}=\frac{2 \left( k^2 \mu _2+\mu _3 \left( \mu _4 w^2-\mu _5 s^2\right) \right) }{\mu _1 \left( k^2 \mu _3 \left( \beta ^2-4 \alpha \gamma \right) +1\right) } \times \nonumber \\{} & {} \quad \times \left\{ -2 \gamma (\alpha +3 \gamma )-\beta ^2+6 \beta \gamma -\frac{24 \gamma ^2 (\alpha -\beta +\gamma )^2}{ B^2\tan ^2 A} + \frac{12 \gamma (\beta -2 \gamma ) (\alpha -\beta +\gamma )}{B \tan A}\right\} , \end{aligned}$$
(27)

where \(A=\frac{1}{2} \sqrt{4 \alpha \gamma -\beta ^2} \left( d+\frac{t^{\omega } \left( k^4 \mu _2 \left( \beta ^2-4 \alpha \gamma \right) +\mu _5 s^2-\mu _4 w^2\right) }{k^3 \mu _3 \omega \left( \beta ^2-4 \alpha \gamma \right) +k \omega }+k x+s z+w y\right) ,\) \(B=\beta -2 \gamma -\sqrt{4 \alpha \gamma -\beta ^2}\).

Set 2.2. Substituting Eq. (26) into Eq. (10), gives

$$\begin{aligned}{} & {} u_{1.5}=2 \beta ^2 \left( k^2 \mu _2+\mu _3 \left( \mu _4 w^2-\mu _5 s^2\right) \right) \times \nonumber \\{} & {} \quad \times \left( (\beta -\gamma ) \exp \left( \beta \left( d+\frac{t^{\omega } \left( \beta ^2 k^4 \mu _2+\mu _5 s^2-\mu _4 w^2\right) }{\omega \left( \beta ^2 k^3 \mu _3+k\right) }+k x+s z+w y\right) \right) \right) \nonumber \\{} & {} \quad \times \frac{ \left( (\gamma -\beta ) \exp \left( \beta \left( d+\frac{t^{\omega } \left( \beta ^2 k^4 \mu _2+\mu _5 s^2-\mu _4 w^2\right) }{\omega \left( \beta ^2 k^3 \mu _3+k\right) }+k x+s z+w y\right) \right) +4\right) -1}{\mu _1 \left( \beta ^2 k^2 \mu _3+1\right) \left( (\beta -\gamma ) \exp \left( \beta \left( d+\frac{t^{\omega } \left( \beta ^2 k^4 \mu _2+\mu _5 s^2-\mu _4 w^2\right) }{\omega \left( \beta ^2 k^3 \mu _3+k\right) }+k x+s z+w y\right) \right) +1\right) {}^2}. \end{aligned}$$
(28)

Set 2.3. Substituting Eq. (26) into Eq. (10), gives

$$\begin{aligned}{} & {} u_{1.6}= -\frac{12 (\alpha -\beta )^2 \left( k^2 \mu _2+\mu _3 \left( \mu _4 w^2-\mu _5 s^2\right) \right) }{\mu _1 \left( \beta ^2 k^2 \mu _3+1\right) \left( -\frac{\alpha }{\beta }+\frac{\exp \left( \beta \left( d+\frac{t^{\omega } \left( \beta ^2 k^4 \mu _2+\mu _5 s^2-\mu _4 w^2\right) }{\omega \left( \beta ^2 k^3 \mu _3+k\right) }+k x+s z+w y\right) \right) }{\beta }+1\right) {}^2}- \nonumber \\{} & {} \quad -\frac{12 \beta (\alpha -\beta ) \left( k^2 \mu _2+\mu _3 \left( \mu _4 w^2-\mu _5 s^2\right) \right) }{\mu _1 \left( \beta ^2 k^2 \mu _3+1\right) \left( -\frac{\alpha }{\beta }+\frac{\exp \left( \beta \left( d+\frac{t^{\omega } \left( \beta ^2 k^4 \mu _2+\mu _5 s^2-\mu _4 w^2\right) }{\omega \left( \beta ^2 k^3 \mu _3+k\right) }+k x+s z+w y\right) \right) }{\beta }+1\right) }\nonumber \\{} & {} \quad -\frac{2 \beta ^2 \left( k^2 \mu _2+\mu _3 \left( \mu _4 w^2-\mu _5 s^2\right) \right) }{\mu _1 \left( \beta ^2 k^2 \mu _3+1\right) }. \end{aligned}$$
(29)

5.2 Analytical solutions for (3+1)-dimensional KdV-BBM equation via the exp\((-\varphi (\xi ))\)-expansion method

Balancing \(u''=N+2\), \(u^2=2N\) one get \(N=2\). The series of sums is as follows when we insert Eq. (12)

$$\begin{aligned} u=B_0+B_1exp(-\varphi (\xi ))+B_2exp(-\varphi (\xi ))^2. \end{aligned}$$
(30)

When paired with Eq. (13), the following system arises.

$$\begin{aligned}{} & {} -6 B_2 c \eta \lambda k^3 \mu _3-2 B_1 c \eta k^3 \mu _3-B_1 c \lambda ^2 k^3 \mu _3+B_1 c k+6 B_2 \eta \lambda k^4 \mu _2 \\{} & {} \quad +2 B_1 \eta k^4 \mu _2+B_1 \lambda ^2 k^4 \mu _2+B_0 B_1 k^2 \mu _1-B_1 \mu _5 s^2+B_1 \mu _4 w^2=0,\\{} & {} \quad -2 B_2 c \eta ^2 k^3 \mu _3-B_1 c \eta \lambda k^3 \mu _3+B_0 c k+2 B_2 \eta ^2 k^4 \mu _2+B_1 \eta \lambda k^4 \mu _2\\{} & {} \quad +\frac{1}{2} B_0^2 k^2 \mu _1-B_0 \mu _5 s^2+B_0 \mu _4 w^2=0,\\{} & {} \quad -10 B_2 c \lambda k^3 \mu _3-2 B_1 c k^3 \mu _3+10 B_2 \lambda k^4 \mu _2+2 B_1 k^4 \mu _2+B_1 B_2 k^2 \mu _1=0,\\{} & {} \quad -8 B_2 c \eta k^3 \mu _3-4 B_2 c \lambda ^2 k^3 \mu _3-3 B_1 c \lambda k^3 \mu _3+B_2 c k+8 B_2 \eta k^4 \mu _2+4 B_2 \lambda ^2 k^4 \mu _2\\{} & {} \quad +3 B_1 \lambda k^4 \mu _2+\frac{1}{2} B_1^2 k^2 \mu _1+B_0 B_2 k^2 \mu _1-B_2 \mu _5 s^2+B_2 \mu _4 w^2=0,\\{} & {} \quad -6 B_2 c k^3 \mu _3+6 B_2 k^4 \mu _2+\frac{1}{2} B_2^2 k^2 \mu _1=0. \end{aligned}$$

For \(B_0\), \(B_1\), \(B_2\) and c, we have two cases and two sets of solution in this instance.

Case 3.

$$\begin{aligned} B_0= & {} \frac{2 \left( 2 \eta +\lambda ^2\right) \left( k^2 \mu _2+\mu _3 \left( \mu _4 w^2-\mu _5 s^2\right) \right) }{\mu _1 \left( k^2 \mu _3 \left( 4 \eta -\lambda ^2\right) -1\right) };\ \ B_1=\frac{12 \lambda \left( k^2 \mu _2+\mu _3 \left( \mu _4 w^2-\mu _5 s^2\right) \right) }{\mu _1 \left( k^2 \mu _3 \left( 4 \eta -\lambda ^2\right) -1\right) };\nonumber \\ B_2= & {} \frac{12 \left( k^2 \mu _2+\mu _3 \left( \mu _4 w^2-\mu _5 s^2\right) \right) }{\mu _1 \left( k^2 \mu _3 \left( 4 \eta -\lambda ^2\right) -1\right) };\ \ c=\frac{k^4 \mu _2 \left( 4 \eta -\lambda ^2\right) -\mu _5 s^2+\mu _4 w^2}{k^3 \mu _3 \left( 4 \eta -\lambda ^2\right) -k}. \end{aligned}$$
(31)

Substituting the conditions in Step 2:, the solutions are as follows:

Set 3.1.

For \(\eta \ne 0\), and \(\lambda ^2-4\eta >0\),

$$\begin{aligned} u_{2.1}= & {} \frac{2 A_1 \left( 2 \eta +\lambda ^2\right) }{C_1}+\frac{48 A_1 \eta ^2}{C_1 \left( -\sqrt{\lambda ^2-4 \eta } \tanh \left( \frac{1}{2} \sqrt{\lambda ^2-4 \eta } \left( C_2+h+k x+s z+w y\right) \right) -\lambda \right) ^2}+\nonumber \\{} & {} \quad \frac{24 A_1 \eta \lambda }{C_1 \left( -\sqrt{\lambda ^2-4 \eta } \tanh \left( \frac{1}{2} \sqrt{\lambda ^2-4 \eta } \left( C_2+h+k x+s z+w y\right) \right) -\lambda \right) }, \end{aligned}$$
(32)

for \(\eta \ne 0\), and \(\lambda ^2-4\eta <0\),

$$\begin{aligned} u_{2.2}= & {} \frac{2 A_1 \left( 2 \eta +\lambda ^2\right) }{C_1}+\frac{48 A_1 \eta ^2}{C_1 \left( \sqrt{4 \eta -\lambda ^2} \tan \left( \frac{1}{2} \sqrt{4 \eta -\lambda ^2} \left( C_2+h+k x+s z+w y\right) \right) -\lambda \right) ^2}+\nonumber \\{} & {} \quad \frac{24 A_1 \eta \lambda }{C_1 \left( \sqrt{4 \eta -\lambda ^2} \tan \left( \frac{1}{2} \sqrt{4 \eta -\lambda ^2} \left( C_2+h+k x+s z+w y\right) \right) -\lambda \right) }, \end{aligned}$$
(33)

for \(\eta =0\), \(\lambda \ne 0\), and \(\lambda ^2-4\eta >0\),

$$\begin{aligned} u_{2.3}= & {} \frac{2 A_1 \lambda ^2}{\mu _1 \left( -k^2 \lambda ^2 \mu _3-1\right) }\nonumber \\{} & {} +\quad \frac{12 A_1 \lambda ^2}{\mu _1 \left( -k^2 \lambda ^2 \mu _3-1\right) \left( \sinh \left( \lambda \left( C_3+h+k x+s z+w y\right) \right) +\cosh \left( \lambda \left( C_3+h+k x+s z+w y\right) \right) -1\right) ^2}\nonumber \\{} & {} +\frac{12 A_1 \lambda ^2}{\mu _1 \left( -k^2 \lambda ^2 \mu _3-1\right) \left( \sinh \left( \lambda \left( C_3+h+k x+s z+w y\right) \right) +\cosh \left( \lambda \left( C_3+h+k x+s z+w y\right) \right) -1\right) },\nonumber \\ \end{aligned}$$
(34)

for \(\eta \ne 0\), \(\lambda \ne 0\), and \(\lambda ^2-4\eta =0\),

$$\begin{aligned} u_{2.4}=-\frac{3 A_1 \lambda ^4 \left( -C_4+h+k x+s z+w y\right) ^2}{\mu _1 \left( \lambda \left( -C_4+h+k x+s z+w y\right) +2\right) ^2}+\frac{6 A_1 \lambda ^3 \left( -C_4+h+k x+s z+w y\right) }{\mu _1 \left( \lambda \left( -C_4+h+k x+s z+w y\right) +2\right) }-\frac{12 A_1 \eta }{\mu _1},\nonumber \\ \end{aligned}$$
(35)

for \(\eta =0\), \(\lambda =0\), and \(\lambda ^2-4\eta =0\),

$$\begin{aligned} u_{2.5}=\frac{12 A_1}{\mu _1 \left( -4 \eta k^2 \mu _3-1\right) \left( C_5+h+k x+s z+w y\right) ^2}+\frac{8 A_1 \eta }{\mu _1 \left( -4 \eta k^2 \mu _3-1\right) }, \end{aligned}$$
(36)

and hence

$$\begin{aligned} A_1= & {} k^2 \mu _2+\mu _3 \left( \mu _4 w^2-\mu _5 s^2\right) ,C_1=\mu _1 \left( k^2 \mu _3 \left( 4 \eta -\lambda ^2\right) -1\right) , C_2=\frac{t^{\omega } \left( k^4 \mu _2 \left( 4 \eta -\lambda ^2\right) -\mu _5 s^2+\mu _4 w^2\right) }{\omega \left( k^3 \mu _3 \left( 4 \eta -\lambda ^2\right) -k\right) },\\ C_3= & {} \frac{t^{\omega } \left( -k^4 \lambda ^2 \mu _2-\mu _5 s^2+\mu _4 w^2\right) }{\omega \left( -\lambda ^2 k^3 \mu _3-k\right) }, C_4=\frac{t^{\omega } \left( \mu _4 w^2-\mu _5 s^2\right) }{k \omega }, C_5=\frac{t^{\omega } \left( -4 \eta k^4 \mu _2-\mu _5 s^2+\mu _4 w^2\right) }{\omega \left( -4 \eta k^3 \mu _3-k\right) }. \end{aligned}$$

Case 4.

$$\begin{aligned} B_0= & {} -\frac{12 \eta \left( k^2 \mu _2+\mu _3 \left( \mu _4 w^2-\mu _5 s^2\right) \right) }{\mu _1 \left( k^2 \mu _3 \left( 4 \eta -\lambda ^2\right) +1\right) };\ \ B_1=-\frac{12 \lambda \left( k^2 \mu _2+\mu _3 \left( \mu _4 w^2-\mu _5 s^2\right) \right) }{\mu _1 \left( k^2 \mu _3 \left( 4 \eta -\lambda ^2\right) +1\right) };\nonumber \\ B_2= & {} -\frac{12 \left( k^2 \mu _2+\mu _3 \left( \mu _4 w^2-\mu _5 s^2\right) \right) }{\mu _1 \left( k^2 \mu _3 \left( 4 \eta -\lambda ^2\right) +1\right) };\ \ c=\frac{k^4 \mu _2 \left( 4 \eta -\lambda ^2\right) +\mu _5 s^2-\mu _4 w^2}{k^3 \mu _3 \left( 4 \eta -\lambda ^2\right) +k}. \end{aligned}$$
(37)

Set 4.1.

For \(\eta \ne 0\), and \(\lambda ^2-4\eta >0\),

$$\begin{aligned} u_{2.6}= & {} -\frac{12 A_1 \eta }{D_1 \mu _1}-\frac{48 A_1 \eta ^2}{D_1 \mu _1 \left( -\sqrt{\lambda ^2-4 \eta } \tanh \left( \frac{1}{2} \sqrt{\lambda ^2-4 \eta } \left( D_2+h+k x+s z+w y\right) \right) -\lambda \right) ^2}\nonumber \\{} & {} \quad -\frac{24 A_1 \eta \lambda }{D_1 \mu _1 \left( -\sqrt{\lambda ^2-4 \eta } \tanh \left( \frac{1}{2} \sqrt{\lambda ^2-4 \eta } \left( D_2+h+k x+s z+w y\right) \right) -\lambda \right) }, \end{aligned}$$
(38)

for \(\eta \ne 0\), and \(\lambda ^2-4\eta <0\),

$$\begin{aligned} u_{2.7}= & {} -\frac{12 A_1 \eta }{D_1 \mu _1}-\frac{48 A_1 \eta ^2}{D_1 \mu _1 \left( \sqrt{4 \eta -\lambda ^2} \tan \left( \frac{1}{2} \sqrt{4 \eta -\lambda ^2} \left( D_2+h+k x+s z+w y\right) \right) -\lambda \right) ^2}\nonumber \\{} & {} -\quad \frac{24 A_1 \eta \lambda }{D_1 \mu _1 \left( \sqrt{4 \eta -\lambda ^2} \tan \left( \frac{1}{2} \sqrt{4 \eta -\lambda ^2} \left( D_2+h+k x+s z+w y\right) \right) -\lambda \right) }, \end{aligned}$$
(39)

for \(\eta =0\), \(\lambda \ne 0\), and \(\lambda ^2-4\eta >0\),

$$\begin{aligned} u_{2.8}= & {} -\frac{12 A_1 \lambda ^2}{\mu _1 \left( 1-k^2 \lambda ^2 \mu _3\right) \left( \sinh \left( \lambda \left( D_3+h+k x+s z+w y\right) \right) +\cosh \left( \lambda \left( D_3+h+k x+s z+w y\right) \right) -1\right) ^2}\nonumber \\{} & {} \quad -\frac{12 A_1 \lambda ^2}{\mu _1 \left( 1-k^2 \lambda ^2 \mu _3\right) \left( \sinh \left( \lambda \left( D_3+h+k x+s z+w y\right) \right) +\cosh \left( \lambda \left( D_3+h+k x+s z+w y\right) \right) -1\right) },\nonumber \\ \end{aligned}$$
(40)

for \(\eta \ne 0\), \(\lambda \ne 0\), and \(\lambda ^2-4\eta =0\),

$$\begin{aligned} u_{2.9}=-\frac{3 A_1 \lambda ^4 \left( D_4+h+k x+s z+w y\right) ^2}{\mu _1 \left( \lambda \left( D_4+h+k x+s z+w y\right) +2\right) ^2}+\frac{6 A_1 \lambda ^3 \left( D_4+h+k x+s z+w y\right) }{\mu _1 \left( \lambda \left( D_4+h+k x+s z+w y\right) +2\right) }-\frac{12 A_1 \eta }{\mu _1}, \end{aligned}$$
(41)

for \(\eta =0\), \(\lambda =0\), and \(\lambda ^2-4\eta =0\),

$$\begin{aligned} u_{2.10}=-\frac{12 A_1}{\mu _1 \left( 1-4 \eta k^2 \mu _3\right) \left( D_5+h+k x+s z+w y\right) ^2}, \end{aligned}$$
(42)

where

$$\begin{aligned}{} & {} A_1=k^2 \mu _2+\mu _3 \left( \mu _4 w^2-\mu _5 s^2\right) , D_1=k^2 \mu _3 \left( 4 \eta -\lambda ^2\right) +1, D_2=\frac{t^{\omega } \left( k^4 \mu _2 \left( 4 \eta -\lambda ^2\right) +\mu _5 s^2-\mu _4 w^2\right) }{\omega \left( k^3 \mu _3 \left( 4 \eta -\lambda ^2\right) +k\right) },\nonumber \\{} & {} \quad D_3=\frac{t^{\omega } \left( -k^4 \lambda ^2 \mu _2+\mu _5 s^2-\mu _4 w^2\right) }{\omega \left( k-k^3 \lambda ^2 \mu _3\right) }, D_4=\frac{t^{\omega } \left( \mu _5 s^2-\mu _4 w^2\right) }{k \omega }, D_5=\frac{t^{\omega } \left( -4 \eta k^4 \mu _2+\mu _5 s^2-\mu _4 w^2\right) }{\omega \left( k-4 \eta k^3 \mu _3\right) }. \end{aligned}$$

6 Graphical representations

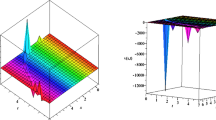
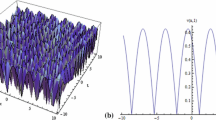
By selecting appropriate values for the unknown parameters, numerous graphs are displayed in this study using Mathematica. The results reveal that Eqs. (23) and (32) are dark soliton, Eqs. (24), (27), (33), and (39) are periodic, Eqs. (25), (34), and (40) are hyperbolic function, Eqs.(28), and (29) are exponential function, and Eqs. (35), (36), (41), and (42) are lump soliton solutions.

For Eqs. (23), (24), (25), (27), (28), (29), (32) and (38), the 3D, contour and 2D plots are shown in Figs. 1, 2, 3, 4, 5. Wave structures are significant in the realm of engineering and physical sciences. All of the solutions obtained are novel and do not exist in the literature.

  • Figure 1 with (a) and (b) for \(\alpha =0.1,\beta =0.1, \gamma =0.72, d=0.27,k=-0.17, \mu _1=-0.33,\mu _2=-0.45, \mu _3=0.61, \mu _4=0.77, s=0.28, w=0.19, y=0.15, z=0.15, \mu _5=0.24,\) and \(\omega =0.95\), (c) \(t=0.35\).

  • Figure 2 with (a) and (b) for \(\beta =0.1, \gamma =0.72, d=0.97, k=-0.17,\mu _1=-0.33, \mu _2=-0.45,\mu _3=0.61, \mu _4=0.77, \mu _5=-0.24, s=0.1, w=0.19,y=0.13, z=0.17,\) and \(\omega =0.65\), (c) \(t=0.35\).

  • Figure 3 with (a) and (b) for \(\alpha =2, \beta =1, d=0.97, k=0.17, \mu _1=-0.43, \mu _2=0.55, \mu _3=-0.81, \mu _4=0.37, s=0.38, w=0.19, y=0.25, z=0.15, \mu _5=0.14,\) and \(\omega =0.65\), (c) \(t=0.35\).

  • Figure 4 with (a) and (b) for \(k=1.5,w=1,s=0.01,y=0.1,z=-0.5,\mu _1=\mu _3=\mu _4=\mu _5=0.1,\mu _2=0.5,\lambda =1,\eta =0.1,h=0.9,\omega =0.95\), (c) \(t=0.55\).

  • Figure 5 with (a) and (b) for \(k=1.4,w=-0.5,s=0.1,y=0.1,z=0.1,\mu _1=0.2,\mu _2=\mu _5=0.1,\mu _3=0.1,\mu _4=0.3,\lambda =0.99,\eta =0.1,h=0.4,\omega =0.95\), (c) \(t=0.95\).

The outcomes show that the suggested methods will help the other associated strong nonlinear models, leading to some novel soliton solutions. As a result, it is clear that the findings in this study provide new knowledge to the existing literature because of their significance in the areas mentioned.

Fig. 1
figure 1

The surface graphs of modified generalized Kudryashov solution \(u_{1.1}\) of Eq. (23)

Full size image
Fig. 2
figure 2

The surface graphs of modified generalized Kudryashov solution \(u_{1.2}\) of Eq. (24)

Full size image
Fig. 3
figure 3

The surface graphs of modified generalized Kudryashov solution \(u_{1.3}\) of Eq. (25)

Full size image
Fig. 4
figure 4

The surface graphs of exp\((-\varphi (\xi ))\)-expansion solution \(u_{2.1}\) of Eq. (32)

Full size image
Fig. 5
figure 5

The surface graphs of exp\((-\varphi (\xi ))\)-expansion solution \(u_{2.6}\) of Eq. (38)

Full size image

7 Sensitivity assessment

In order to analyze the sensitivity of the generalized KdV-BBM model in Eq. (1), the Galilean operator for Eq. (20) results the following dynamical system:

$$\begin{aligned} \begin{array}{l} \frac{d u}{d \xi }=\phi ,\\ \frac{d \phi }{d \xi }=\frac{-2 c k u(\xi )-k^2 \mu _1 u(\xi )^2+2 \mu _5 s^2 u(\xi )-2 \mu _4 w^2 u(\xi )}{2 k^3 \left( k \mu _2-c \mu _3\right) }. \end{array} \end{aligned}$$
(43)

The dynamical system is of low sensitivity if a small change in starting values gives a slight modification in the system dynamics. The critical points of the given system will be the origin and \((-\frac{2 \left( c k-\mu _5 s^2+\mu _4 w^2\right) }{k^2 \mu _1},0)\). Based on the trial values: \(c=-1\), \(k=1.2\), \(w=0.8\), and \(s=\mu _i=1\), the initial positions and velocities of the system are considered to be closed to the origin as follows: \({P_1}=(0.1,0)\), \({P_2}=(0.15,0)\), and \({P_3}=(0.2,0)\), the solutions are illustrated in Fig. 6a. The influence, with \({P_1}=(0.85,0.1)\), \({P_2}=(0.9,0.075)\), and \({P_3}=(0.95,0.05)\) is also considered in Fig. 6b, subject to the parameters \(c=-0.8\), \(k=1.35\), \(w=0.5\), \(s=0.3\), and \(\mu _i=1\). The critical point in this case is approximately (1, 0).

Fig. 6
figure 6

Sensitivity assessment for different initial data

Full size image

8 Conclusion

The modified generalized Kudryashov and exp(-\(\varphi (\xi \)))-expansion methods are used to derive entirely new soliton solutions to the combined KdV-BBM equations. To understand the fundamental significance of the suggested approaches through some solitons, graphical representations in 3D, contour, and 2D plots, as illustrated in Figs. 1, 2, 3, 4, 5, are provided. These solutions are expected to play a significant role in understanding the dynamics of this model and capturing some of its physical properties. The methods show the power and efficiency of producing new exact solutions for a large class of nonlinear fractional evolution equations. It is also important to note that the obtained exact solutions are plugged back into the original equation to verify the accuracy of retrieved solutions. In addition, the sensitivity effectiveness for the corresponding dynamical system is discussed. It has been shown that the methods are quite successful and can be used to solve various forms of NFPDEs in many fields of physics, engineering, and mathematics. The obtained solutions may benefit some real-world situations or in particular geographic areas, including coastal constructions or additional environmental factors. They could also be used to study the energy transfer and subsequent wave patterns in nonlinear interactions between solitary waves. This might have an impact on how waves behave in coastal areas, including how solitary waves might affect sediment transfer, erosion along the coast, or the layout of coastal constructions. In conclusion, this work has the potential to further our understanding of shallow water wave dynamics and offer insightful information for both theoretical and practical applications in the future.