Analytical and numerical studies of the modified Kawahara equation with dual-power law nonlinearities

Abstract

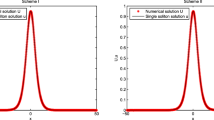
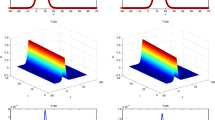
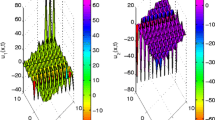
In this article, the Kawahara and modified Kawahara equations with dual-power law nonlinearities are solved based on the sine-cosine method and finite difference schemes. The fourth-order accurate difference scheme for the Kawahara equation and the second-order accurate difference scheme for the modified Kawahara equation have been constructed. The difference schemes have energy conservative properties. The existence, uniqueness, stability, and convergence of the numerical solutions are all well established. Finally, some numerical experiments demonstrate the reliability of the theoretical statements. Also, comparisons between the solutions obtained from the exact solitary wave solutions and the linearly finite difference schemes are made to demonstrate that the present schemes are efficient and reliable, and can simulate the single or multi-solitary waves propagating at a long period.

Appendix

In this appendix, we prove that the initial and boundary value problem (1.1)–(1.4) is well-posed.

Theorem A.1

Suppose $u_{0}\in H_{0}^{2}[x_{l},x_{r}]$ and $u(x,t)\in C_{x,t}^{5,1}([x_{l},x_{r}]\times [0,T])$, then the initial and boundary value problem (1.1)–(1.4) is well-posed.

Proof

First, we assume that $u_{1}$ and $u_{2}$ are two solutions of the problem (1.2)–(1.3) with the boundary condition (1.4) satisfying the initial conditions $u_{0}^{(1)}$ and $u_{0}^{(2)}$, respectively. Let $\eta =u_{1}-u_{2}$, then $\eta$ satisfies the following equation

$$\begin{aligned} \eta _{t}= & {} -\alpha (p+1)[(u_{1})^{p-1}(u_{1})_{x}(u_{1})_{xx}-(u_{2})^{p-1}(u_{2})_{x}(u_{2})_{xx}] -\alpha [(u_{1})^{p}(u_{1})_{xxx}\nonumber \\{} & {} -(u_{2})^{p}(u_{2})_{xxx}] -\beta [(u_{1})^{m}(u_{1})_{x}-(u_{2})^{m}(u_{2})_{x}]-\eta _{xxxxx}, \end{aligned}$$

(A.1)

with the initial condition

$$\begin{aligned} \eta (x,0)=u_{0}^{(1)}-u_{0}^{(2)},~~x\in [x_{l},x_{r}], \end{aligned}$$

(A.2)

and boundary conditions

$$\begin{aligned} \eta (x_{l},t)=\eta (x_{r},t)=0,~~\eta _{x}(x_{l},t)=\eta _{x}(x_{r},t)=0,~~\eta _{xx}(x_{l},t)=\eta _{xx}(x_{r},t)=0. \end{aligned}$$

(A.3)

Introducing the function $\tilde{E}(t)=\displaystyle \int _{x_{l}}^{x_{r}}\eta ^{2}dx$ and by similar arguments as that in the proof of Theorem 2.1, we have

$$\begin{aligned} \frac{d\tilde{E}(t)}{d t}= & {} -2\alpha (p+1)\int _{x_{l}}^{x_{r}}\eta \Big [(u_{1})^{p-1}(u_{1})_{x}(u_{1})_{xx}-(u_{2})^{p-1}(u_{2})_{x}(u_{2})_{xx}\Big ]dx \nonumber \\{} & {} -2\int _{x_{l}}^{x_{r}}\eta \eta _{xxxxx}dx-2\alpha \int _{x_{l}}^{x_{r}}\eta \Big [(u_{1})^{p}(u_{1})_{xxx}-(u_{2})^{p}(u_{2})_{xxx}\Big ]dx \nonumber \\{} & {} -2\beta \int _{x_{l}}^{x_{r}}\eta \Big [(u_{1})^{m}(u_{1})_{x}-(u_{2})^{m}(u_{2})_{x}\Big ]dx. \end{aligned}$$

(A.4)

Since $u(x,t)\in C_{x,t}^{5,1}([x_{l},x_{r}]\times [0,T])$, we let $L=x_{l}-x_{r}$ and suppose that

$$\begin{aligned} M_{0}=\max \{|u|,|u_{x}|,|u_{xx}|,|u_{xxx}|\},~~(x,t)\in [x_{l},x_{r}]\times [0,T]. \end{aligned}$$

Thus, we have

$$\begin{aligned}{} & {} \Big |-2\alpha \int _{x_{l}}^{x_{r}}\eta \Big [(u_{1})^{p}(u_{1})_{xxx}-(u_{2})^{p}(u_{2})_{xxx}\Big ]dx\Big |\le 2\alpha M_{0}\Big |\int _{x_{l}}^{x_{r}}\eta \Big [(u_{1})^{p}-(u_{2})^{p}\Big ]dx\Big | \nonumber \\{} & {} =2\alpha M_{0}\Big |\int _{x_{l}}^{x_{r}}\eta (u_{1}-u_{2})\Big [(u_{1})^{p-1}+(u_{1})^{p-2}u_{2}+\cdot \cdot \cdot +u_{1}(u_{2})^{p-2}+(u_{2})^{p-1}\Big ]dx\Big | \nonumber \\{} & {} \le 2\alpha M_{0}pM^{p-1}_{0}\Big |\int _{x_{l}}^{x_{r}}\eta (u_{1}-u_{2})dx\Big |=2\alpha pM^{p}_{0}\int _{x_{l}}^{x_{r}}\eta ^{2}dx=2\alpha pM^{p}_{0}\tilde{E}(t). \end{aligned}$$

(A.5)

Similarly, we have

$$\begin{aligned}{} & {} \Big |-2\alpha (p+1)\int _{x_{l}}^{x_{r}}\eta \Big [(u_{1})^{p-1}(u_{1})_{x}(u_{1})_{xx}-(u_{2})^{p-1}(u_{2})_{x}(u_{2})_{xx}\Big ]dx\Big | \nonumber \\{} & {} \le 2\alpha (p+1)M_{0}^{2}\Big |\int _{x_{l}}^{x_{r}}\eta \Big [(u_{1})^{p-1}-(u_{2})^{p-1}\Big ]dx\Big | \nonumber \\{} & {} = 2\alpha (p+1)M_{0}^{2}\Big |\int _{x_{l}}^{x_{r}}\eta (u_{1}-u_{2})\Big [(u_{1})^{p-2}+(u_{1})^{p-3}u_{2}+\cdot \cdot \cdot +u_{1}(u_{2})^{p-3}\nonumber \\{} & {} \quad +(u_{2})^{p-2}\Big ]dx\Big | \le 2\alpha (p+1)M_{0}^{2}(p-1)M^{p-2}_{0}\Big |\int _{x_{l}}^{x_{r}}\eta (u_{1}-u_{2})dx\Big | \nonumber \\{} & {} =2\alpha (p^{2}-1)M^{p}_{0}\int _{x_{l}}^{x_{r}}\eta ^{2}dx=2\alpha (p^{2}-1)M^{p}_{0}\tilde{E}(t), \end{aligned}$$

(A.6)

$$\begin{aligned}{} & {} \Big |-2\beta \int _{x_{l}}^{x_{r}}\eta \Big [(u_{1})^{m}(u_{1})_{x}-(u_{2})^{m}(u_{2})_{x}\Big ]dx\Big | \nonumber \\{} & {} \le 2\beta M_{0}\Big |\int _{x_{l}}^{x_{r}}\eta \Big [(u_{1})^{m}-(u_{2})^{m}\Big ]dx\Big |\le 2\beta mM^{m}_{0}\int _{x_{l}}^{x_{r}}\eta ^{2}dx\nonumber \\{} & {} =2\beta mM^{m}_{0}\tilde{E}(t). \end{aligned}$$

(A.7)

Furthermore, we have

$$\begin{aligned} \int _{x_{l}}^{x_{r}}\eta \eta _{xxxxx}dx=\Big [(\eta \eta _{xxxx}-\eta _{x}\eta _{xxx})+\frac{1}{2}(\eta _{xx})^{2}\Big ]\Big |_{x_{l}}^{x_{r}}=0. \end{aligned}$$

(A.8)

Substituting (A.5)–(A.8) into (A.4), we obtain

$$\begin{aligned} \frac{d\tilde{E}(t)}{d t}\le \gamma E^{*}(t),~~t\in [0,T], \end{aligned}$$

which leads to

$$\begin{aligned} \tilde{E}(t)\le \tilde{E}(0)e^{\gamma t}\le \tilde{E}(0)e^{\gamma T}, \end{aligned}$$

where $\gamma =2[\alpha (p^{2}+p-1)M^{p}_{0}+\beta mM^{m}_{0}]$. Thus, if $u_{0}^{(1)}=u_{0}^{(2)}$, we have $\eta (x,0)=0$ and hence $\tilde{E}(0)=0$, implying that $\tilde{E}(t)=0$, $0\le t\le T$. By the Sobolev inequality [44, 45], we obtain $\Vert \eta \Vert _{L_{2}}=0$ and $u_{1}=u_{2}$. Furthermore, if $\eta (x,0)<\varepsilon$, $\eta _{x}(x,0)<\varepsilon$, $\eta _{xx}(x,0)<\varepsilon$, we obtain $\tilde{E}(0)<\varepsilon$ and hence $\tilde{E}(t)\le \tilde{E}(0)e^{\gamma T}\le \varepsilon e^{\gamma T}$, where $0\le t\le T$. That is, the solution is continuously dependent on the initial condition. Thus, the problems (1.1)–(1.4) are well-posed as required. $\square$