1 Introduction

In recent years, the growing demand from customers for top-notch quality and speedy service has introduced new challenges. To be a competitive player in this market, manufacturers are seeking strategic alliances among their supply chain. In this context, evaluating and selecting suppliers to meet the company’s strategic goals play a significant role (Ghadimi et al., 2018). Before 1980, supplier selection was primarily based on costs. However, in recent years, besides economic, environmental and social factors have to be considered simultaneously for supplier assessment (Giri et al., 2022; Hosseini et al., 2022). Due to global environmental pollution, which is of growing concern, environmental criteria are added. Sustainable supplier assessment is crucial for creating a sustainable supply chain (Cantele et al., 2023). To remain competitive in the ever-evolving global market, manufacturers face the imperative of not only satisfying customer requirements but also aligning with the increasingly prominent sustainability expectations of their customers. By embracing sustainability as a core principle, manufacturers can not only secure their position in the global market but also contribute to a more environmentally conscious and socially responsible business landscape. Therefore, the foremost challenge at present is to evaluate the reliability of the supply chain, focusing on its ability to meet customer demand, all the while incorporating considerations for sustainability. This research primarily focuses on the pursuit of supply chain sustainability while simultaneously meeting customer demands, aiming to strike a harmonious balance between these two aspects.

The reliability of the supply chain is the probability that the supply chain meets customer requirements. Various researchers have broadened the scope of reliability by evaluating how well the supply chain fulfills different customer requirements. Beyond simply meeting customer demands, it must also adhere to various specific conditions, such as Yeh et al. (2014) considered supplier production capacity and the damage rate of goods, Lin et al. (2016) added the budget, Huang (2022) assessed the reliability when inventory is available, Tucker and Daskin (2022) took the percentage of expected shortage into account, and Niu et al. (2023) considered the carbon emissions during transport process. To the best of our knowledge, existing literature on reliability and supply chain are not sufficient to address supplier sustainability. This is the first research in the reliability assessment of the supply chain to involve the condition of supplier sustainability.

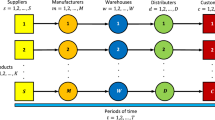
Generally, a supply chain can be described as a network topology with arcs and nodes. Each node in the network represents a supplier, assembly plant, or customer, and the arc connected between the nodes. There are carriers above the arcs. The capacity of individual carriers, as indicated by the availability of delivery containers, should not be considered deterministic, as they could be shared with other customers. More precisely, carriers have distinct sets of potential delivery capacities. Thus, such a network can be regarded as a stochastic flow network (Huang et al., 2022; Nguyen et al., 2023; Xu et al., 2021) to match the real-world. A number of researchers have extensively utilized stochastic flow networks in several real-world, such as computers (Huang et al., 2022), distribution (Niu et al., 2023), and rescue operations (Huang et al., 2023). In this research, a supply chain is also regarded as a typical stochastic flow network and is called a stochastic supply chain network (SSCN).

Recently, several researchers (Huang, 2020; Huang et al., 2022; Nguyen & Lin, 2021; Xu et al., 2021) have evaluated reliability for stochastic flow networks in terms of the concept of minimal path (MP). The MP concept is utilized to compute the lower capacity vectors. The lower capacity vectors required to fulfill the requested flow. Besides, the probability of satisfying the flow can then be determined based on these vectors. This research also involved MP concept and adds the concept of supplier sustainability to an SSCN and assesses the corresponding reliability, defined as the probability that the SSCN can successfully transport sufficient goods to meet the customer demand under budget, supplier production capacity, and supplier sustainability.

This research proposes an algorithm for an SSCN to assess reliability. Such a reliability can be implemented to evaluate the capability of the supply chain. The manager can easily realize the current supply chain situation and make intelligent decisions to determine the order allocation, supplier sustainability level or budget. The remainder of this research is organized as follows. The model is built in Sect. 2, and the proposed algorithm to assess reliability for SSCN is introduced in Sect. 3. The numerical example is illustrated in Sect. 4. Finally, the conclusions are summarized in Sect. 5.

2 Model building

In this section, the SSCN is constructed first. Secondly, the relationship between the flow vector and carrying capacity vector is introduced. Finally, the additional conditions such as supplier sustainability, budget, and supplier production capacity are introduced.

2.1 The construction of an SSCN

In an SSCN, several nodes are represented by multiple suppliers, assembly plants, and customers. Several arcs are linked to the nodes and ei is denoted by ith arc for i = 1, 2, …, n. The carrier above the arc ei is responsible for transporting goods and several states with associated available carrying capacities in it for i = 1, 2, …, n. The maximal carrying capacity of the carrier above arc ei is denoted by φi for i = 1, 2, …, n, and φi = \(\beta_{{i\theta_{i} }} < \, \cdot\cdot\cdot \, < \beta_{i2} < \beta_{i1} = \, 0 \, fori = \, 1, \, 2, \, ...,n\) where βip is the pth carrying capacity of carrier above arc ei for p = 1, 2, …, θi. The concept of the MP is used herein to represent the transport path from the supplier to the customer. The flow vector is denoted as H = (h1, h2, …, hm) with hj being the current flow through jth minimal path Tj for j = 1, 2, …, m and denoting the number of transported goods. The carrying capacity vector is denoted as Y = (y1, y2, …, yn) for the transportation of carrier where yi is the current carrying capacity of carrier above arc ei that can transport for i = 1, 2, …, n. The SSCN further adheres to the following assumptions:

  1. (1)

    The quantity of transported goods should be an integer value in the SSCN.

  2. (2)

    The various carriers' carrying capacities are statistically independent.

  3. (3)

    The quantity of transported goods should follow the flow-conservation law (Ford Jr & Fulkerson, 2015) in the SSCN.

2.2 The relationship between the flow vector and carrying capacity vector

Suppose there are z suppliers, the relationship between the amount of assigned order from the uth supplier and the flow vector H can be further expressed as follows,

$$ \sum\nolimits_{{j:T_{j} \in \delta_{u} }} {h_{j} = a_{u} } ,u = \, 1, \, 2, \, \ldots ,z $$
(1)

where δu represents those minimal paths from the uth supplier to the customer and au represents the amount of assigned order to the uth supplier. \(\sum\nolimits_{{j:T_{j} \in \delta_{u} }} {h_{j} }\) is the number of transported goods from the uth supplier to the customer. Since each order allocation should satisfy the demand D from the customer, such order allocation is feasible if it meets the following equation,

$$ \sum\limits_{u = 1}^{z} {a_{u} = D} . $$
(2)

[Y] is defined as the smallest integer that is larger than or equal to y. Any feasible flow vector H should satisfy the following maximal carrying capacity constraint,

$$ \left\lceil {\alpha \sum\nolimits_{{j:e_{i} \in T_{j} }} {h_{j} } } \right\rceil \le \varphi_{i} ,i = \, 1, \, 2, \, ...,n, $$
(3)

where \(\left\lceil {\alpha \sum\nolimits_{{j:e_{i} \in T_{j} }} {h_{j} } } \right\rceil\) represents the total consumed carrying capacity by the flow through arc ei and α is consumed carrying capacity per unit of flow. Constraint (3) shows that the consumed carrying capacity by the carrier above arc ai should not exceed its maximal carrying capacity. For convenience, let HM be the set of all feasible flow vector H that satisfies constraint (3). Similarly, any H satisfying the following constraint is said to be feasible under the carrying capacity vector Y = (y1, y2, …, yn),

$$ \left\lceil {\alpha \sum\nolimits_{{j:e_{i} \in T_{j} }} {h_{j} } } \right\rceil \le y_{i} ,i = \, 1, \, 2, \, \ldots ,n. $$
(4)

For this reason, HY is the set of H feasible under Y.

2.3 Supplier sustainability and budget in an SSCN

Since the sustainability performance of suppliers is important and cannot be ignored. Several previous researchers have proposed many relevant criteria for assessing supplier sustainability (Ali & Zhang, 2023; Giri et al., 2022; Hosseini et al., 2022; Lo et al., 2021). According to the relevant criteria for assessing supplier sustainability, Khemiri et al. (2017) converted supplier sustainability assessments into order allocation sustainability assessments and further obtained each order allocations sustainability index. Suppose there are v order allocations. An order allocation sustainability index Sw, w = 1, 2,…, v in this research can be generated by applying the same concept. In an SSCN, in order to secure and pursue more sustainable order allocations, such an order allocation sustainability index Sw is feasible if it satisfies

$$ S_{w}\ge L, w= 1,2, \ldots ,v $$
(5)

where L is represented the supplier sustainability level. The order allocation sustainability index Sw is represented as the sustainability performance of its order allocation. Through this index, the performance of this order allocation in terms of sustainability can be evaluated, and better order allocations can be found. Based on the constraint (5), we find the order allocations that meet sustainability requirement. When the supplier sustainability level L is set higher, it means the requirement for sustainability are higher. The order allocation sustainability index Sw equals 1, which corresponds to the reference ideal. Conversely, when Sw equals 0, the performance falls to the extremely poor end of the spectrum. Apart from this, each supplier has its production capacity. Let Pu be the supplier production capacity of the uth supplier for u = 1, 2,…,z. Such an au is feasible if it meets

$$ a_{u} \le P_{u} ,u = \, 1, \, 2, \, \ldots ,z $$
(6)

Furthermore, it should be noted that the unit production cost of uth supplier is denoted by \(B_{u}^{prod}\) and the per unit cost of consumed carrying capacity through arc ei for transportation is denoted by \(B_{i}^{tran}\), i = 1, 2, …, n. The volume of capacity utilized influences the cost of production for a particular supplier, and the total supplier production cost for any flow vector is calculated by adding up the supplier production costs among all suppliers. The carrier transport cost for a particular arc is influenced by the volume of capacity utilized, and the total carrier transport cost for any flow vector is computed by adding up the carrier transport costs along all arcs. The total cost consists of the total supplier production cost and the total carrier transport cost. Thus, any flow vector H is within the budget C if and only if it satisfies

$$ \sum\nolimits_{u = 1}^{z} {\left( {B_{u}^{prod} \sum\nolimits_{{j:T_{j} \in \delta_{u} }} {h_{j} } } \right)} + \sum\nolimits_{i = 1}^{n} {B_{i}^{tran} \left\lceil {\alpha \sum\nolimits_{{j:e_{i} \in T_{j} }} {h_{j} } } \right\rceil } \le C, $$
(7)

where \(B_{u}^{prod} \sum\nolimits_{{j:T_{j} \in \delta_{u} }} {h_{j} }\) represents the supplier production cost that uth supplier provides \(\sum\nolimits_{{j:T_{j} \in \delta_{u} }} {h_{j} }\) goods and \(B_{i}^{tran} \left\lceil {\alpha \sum\nolimits_{{j:e_{i} \in T_{j} }} {h_{j} } } \right\rceil\) denotes the carrier transport cost through arc ei. Constraint (7) requires that the total cost cannot exceed budget C.

3 Reliability for an SSCN

In this work, the reliability is defined for an SSCN firstly and then an algorithm is developed for reliability evaluation.

3.1 Definition of reliability

The reliability RD,C,L is the probability that the SSCN meets the demand D, budget C, and the supplier production capacity while maintaining supplier sustainability level L in the SSCN. At a certain supplier production capacity, let ρ ≡ {Y|Y satisfies all requirements of the demand D, budget C and supplier sustainability level L}. The reliability RD,C,L can be represented as

$$ R_{D,C,L} = \sum\limits_{{Y \in {{\varvec{\uprho}}}}} {\Pr \left\{ Y \right\}} $$
(8)

By the assumption 2, Pr{Y} can be calculated as \(\prod\nolimits_{i = 1}^{n} {\Pr \left\{ {y_{i} } \right\}}\). However, when the network is of considerable magnitude, it becomes impractical to search for all feasible Y and aggregate their corresponding probabilities to determine RD,C,L. In order to efficiently determine RD,C,L, the minimal carrying vector (MCV) is defined as if Y ∈ ρ and any carrying capacity vector Z with Z < Y such that Z ∉ ρ, then Y is called an MCV. That is, an MCV is the minimal one from ρ. Additionally, the relationships between any two carrying capacity vectors Y and Z are further defined as follows,

  • Y ≤ Z: (y1, y2, …, yn) ≤ (z1, z2, …, zn) if and only if yi ≤ zi for each i.

  • Y < Z: if and only if Y ≤ Z and yi < zi for at least one i.

Each Y transformed from an H is considered as an MCV candidate by Eq. (4). To clarify the situation, let Ψ be the set of MCV candidates and Ψmin = {Y|Y is minimal in Ψ}. For finding all MCVs, suppose there are q MCV candidates generated from F. The set Ψmin is obtained as follows.

figure a

Suppose we obtained q MCVs: Y1, Y2, …, Yq. Then, the reliability RD,C,L can be revised as:

$$ R_{D,C,L} = \Pr \left\{ {\bigcup\limits_{i = 1}^{q} {\left\{ {Y|Y \ge Y_{i} } \right\}} } \right\}. $$
(9)

Various approaches can be employed to Eq. (9), including the state-space decomposition (Aven, 1985), the inclusion–exclusion principle (Hudson & Kapur, 1985), the Recursive Sum of Disjoint Products (RSDP) (Zuo et al., 2007), and the RSDP with ordering (Bai et al., 2015). Zuo et al. (2007) compared the corresponding approaches and showed the efficiency of RSDP. Bai et al. (2015) further proposed the RSDP with ordering and compared with the RSDP. The results also indicated that the efficiency of the RSDP with ordering. Thus, the RSDP with ordering is applied to determine the reliability RD,C,L herein.

3.2 Proposed algorithm for reliability calculation

The flowchart of the proposed algorithm is shown in Fig. 1. For all MPs, the supplier sustainability assessment and supplier production capacity, carrier transport cost, and supplier production cost are known in advance in an SSCN. Given demand D, budget C, and supplier sustainability level L, an algorithm is developed to evaluate reliability for an SSCN as follows.

Fig. 1
figure 1

The flowchart of the proposed algorithm

Full size image

Reliability algorithm//Evaluate reliability for an SSCN.

Input: D, C, L

Step 1 Find all order allocation under following condition:

1.1 There are v order allocation, and each order allocation is meeting the demand D.

$$ \sum\limits_{u = 1}^{z} {a_{u} = D} $$
(10)

1.2 Each the amount of assigned order au is meeting supplier production capacity Pu.

$$ a_{u} \le P_{u} ,u = { 1},{ 2}, \, \ldots ,z $$
(11)

If not, delete the order allocation.

1.3 According to each order allocation’s order allocation sustainability index Sw, the order allocation is meeting the supplier sustainability level L.

$$ S_{w}\geq L, w= 1,2, \ldots ,v $$
(12)

If not, delete the order allocation.

Step 2 Transform the amount of assigned order au from the assigned supplier into the flow vector H = (h1, h2, …, hm).

$$ \sum\nolimits_{{j:T_{j} \in \delta_{u} }} {h_{j} = a_{u} } ,u = { 1},{ 2}, \, \ldots ,z. $$
(13)

Step 3 Check each flow vector H which is transformed in step 2 whether it satisfies the following constraints.

3.1 The carriers’ maximal carrying capacity constraint

$$ \left\lceil {\alpha \sum\nolimits_{{j:e_{i} \in T_{j} }} {h_{j} } } \right\rceil \le \varphi_{i} ,i = { 1},{ 2}, \, ...,n, $$
(14)

If not, delete the flow vector H.

3.2 Budget constraint

$$ \sum\nolimits_{u = 1}^{z} {\left( {B_{u}^{prod} \sum\nolimits_{{j:T_{j} \in \delta_{u} }} {h_{j} } } \right)} + \sum\nolimits_{i = 1}^{n} {B_{i}^{tran} \left\lceil {\alpha \sum\nolimits_{{j:e_{i} \in T_{j} }} {h_{j} } } \right\rceil } \le C, $$
(15)

If not, delete the flow vector H.

Step 4 Transform each feasible flow vector H from step 3 into carrying capacity vector Y = (y1, y2, …, yn) via

$$ y_{i} = \beta_{ip} {\text{where}}\beta_{{i(p - {1})}} \left\lceil {\alpha \sum\nolimits_{{j:e_{i} \in T_{j} }} {h_{j} } } \right\rceil \le \beta_{ip} ,i = { 1},{ 2}, \, \ldots ,n $$
(16)

Step 5 Each Y is an MCV candidate, and check each Y whether it is an MCV by the comparison process.

Step 6 Suppose there are q MCVs: Y1, Y2,…,Yq are obtained from step 5, use RSDP with ordering to derive the reliability RD,C,L = \(\Pr \left\{ {\bigcup\nolimits_{i = 1}^{q} {\left\{ {Y|Y \ge Y_{i} } \right\}} } \right\}.\)

Output: RD, C, L

3.3 Computational complexity analysis

In the proposed algorithm, the number of solutions to Eq. (10) is λ ≡ \(\left( {\begin{array}{*{20}c} {m + D - 1} \\ D \\ \end{array} } \right)\) in the worst case.

3.3.1 Computational complexity of steps 1 and 2

Step 1 is executed to find all order allocations, and Step 2 transforms the order allocation into a flow vector. Each solution of Eqs. (10)–(13) needs at most O(z) time. Thus, Steps 1 to 2 need at most O(z·λ) time to generate all flow vectors.

3.3.2 Computational complexity of step 3

Each solution of Eq. (14) needs at most O(n) to examine whether it exceeds the carriers’ maximal carrying capacity or not. Each solution of Eq. (15) needs at most O(n·m) to examine whether it exceeds the budget. Therefore, Step 3 takes O(n·m·λ) time to obtain all feasible flow vector in the worst case.

3.3.3 Computational complexity of step 4

Each flow vector takes O(n) time to transform into the carrying capacity vector. Therefore, step 4 needs O(n·λ) time to obtain all carrying capacity vector in the worst case as the number |Ψ| of MCV is at most λ.

3.3.4 Computational complexity of step 5

Step 5 is to remove the non-minimal ones in Ψ. The comparison process takes at most O(n·λ) time to test one candidate whether it is smaller than another or not, and thus O(n·λ2) time for all candidates. In the worst cast, step 5 takes O(n·λ2) time to implement the comparison process.

3.3.5 Computational complexity of step 6

Step 6 spends O(n) time to execute the RSDP with ordering for each MCV in the worst case. Therefore, it takes at most O(n·λ) as the number |Ψ| of MCV is at most λ.

In summary, given that \(\lambda \equiv \left( {\begin{array}{*{20}c} {m + D - 1} \\ D \\ \end{array} } \right) = \frac{(m + D - 1) \times (m + D - 2) \times ... \times m}{{D \times (D - 1) \times ... \times 2 \times 1}}\) it implies λ >  > m. The number m of minimal path is at most n. Moreover, the number z of suppliers in general is always less than m. Therefore, the computational complexity of the proposed algorithm in the worst case is O(z·λ) + O(n·m·λ) + O(n·λ) + O(n·λ2) + O(n·λ) = O(n·λ2) time.

4 A numerical example

A supply chain network for an SSCN shown in Fig. 2 is adopted to illustrate the proposed algorithm. In this example, there are three suppliers, two assembly plants, and customer with eight arcs. The MP for each supplier, and related production capacity and cost are listed in Table 1. Table 2 shows the data of available capacities and probability distributions of the eight arcs a. In this SSCN, the consumed carrier capacity per unit of commodity is 0.7, i.e., α = 0.7.

Fig. 2
figure 2

An illustrative SSCN

Full size image
Table 1 The related data for each supplier
Full size table
Table 2 The data of the carriers on arcs
Full size table

4.1 An illustration for the proposed algorithm

In the SSCN shown in Fig. 1, Demand of customer is 5. Under demand D = 5, budget C = 5600, and supplier sustainability level L = 0.75, the following procedure presents reliability evaluation with all MCV generation.

Step 1 Find all order allocation under following condition:

1.1. Due to \(\sum\nolimits_{u = 1}^{3} {a_{u} = 5}\), there are 21 order allocations listed in the first column of Table 3.

Table 3 The results from step 1.1 to 1.3
Full size table

1.2. Each the amount of assigned order au is meeting supplier production capacity

$$ \begin{gathered} a_{1} \le 3, \hfill \\ a_{2} \le 2, \hfill \\ a_{3} \le 3. \hfill \\ \end{gathered} $$

There are 9 order allocations shown in the second column of Table 3.

1.3. Each order allocation’s order allocation sustainability index Sw is shown in Table 3. By Sw ≥ 0.75, a total of 5 order allocations are reserved in the third column of Table 3.

Step 2 According to selected order allocation from step 1, transform the amount of assigned order au from the assigned supplier into the flow vector H = (h1, h2, …, h6). Take order allocation (3, 2, 0) as an example,

$$ \begin{gathered} h_{1} + h_{2} = 3, \hfill \\ h_{3} + h_{4} = 2, \hfill \\ h_{5} + h_{6} = 0. \hfill \\ \end{gathered} $$

Then, there are totally 78 feasible flow vectors.

Step 3 Check each flow vector which is transformed in step 2 whether it satisfies the following two constraints.

3.1 The carriers’ maximal carrying capacity constraint

$$ \begin{gathered} \left\lceil {{0}{\text{.7}} \times h_{1} } \right\rceil \le 4, \, \left\lceil {{0}{\text{.7}} \times h_{2} } \right\rceil \le 3, \hfill \\ \left\lceil {{0}{\text{.7}} \times h_{3} } \right\rceil \le 4, \, \left\lceil {{0}{\text{.7}} \times h_{4} } \right\rceil \le 3, \hfill \\ \left\lceil {{0}{\text{.7}} \times h_{5} } \right\rceil \le 4, \, \left\lceil {0.7 \times h_{6} } \right\rceil \le 2, \hfill \\ \left\lceil {{0}{\text{.7}} \times h_{1} + {0}{\text{.7}} \times h_{3} + {0}{\text{.7}} \times h_{5} } \right\rceil \le 4, \hfill \\ \left\lceil {{0}{\text{.7}} \times h_{2} + {0}{\text{.7}} \times h_{4} + {0}{\text{.7}} \times h_{6} } \right\rceil \le 3. \, \hfill \\ \end{gathered} $$

3.2 Budget constraint

$$ \begin{gathered} 150 \times \left( {h_{1} + h_{2} } \right) + 175 \times \left( {h_{3} + h_{4} } \right) + 200 \times \left( {h_{5} + h_{6} } \right) \hfill \\ + 480 \times \left\lceil {{0}{\text{.7}} \times h_{1} } \right\rceil + 450 \times \left\lceil {{0}{\text{.7}} \times h_{2} } \right\rceil + 650 \times \left\lceil {{0}{\text{.7}} \times h_{3} } \right\rceil \hfill \\ { + 550} \times \left\lceil {{0}{\text{.7}} \times h_{4} } \right\rceil + 600 \times \left\lceil {{0}{\text{.7}} \times h_{5} } \right\rceil + 585 \times \left\lceil {{0}{\text{.7}} \times h_{6} } \right\rceil \hfill \\ + 500 \times \left\lceil {{0}{\text{.7}} \times h_{1} + {0}{\text{.7}} \times h_{3} + {0}{\text{.7}} \times h_{5} } \right\rceil \hfill \\ + 515 \times \left\lceil {{0}{\text{.7}} \times h_{{2}} + {0}{\text{.7}} \times h_{{4}} + {0}{\text{.7}} \times h_{6} } \right\rceil \hfill \\ \le {5600}. \hfill \\ \end{gathered} $$

After checking, a total of 11 feasible flow vectors are obtained and are listed in the first column of Table 4.

Table 4 The results from step 3 to 4
Full size table

Step 4 Each feasible H from step 3 is transformed into Y = (y1, y2,…,y8) via,

$$ \begin{gathered} \left\{ {\begin{array}{*{20}c} {y_{1} = \beta_{1p} ,} & {{\text{if }}\beta_{1(p - 1)} { < }\left\lceil {{0}{\text{.7}} \times h_{1} } \right\rceil \le \beta_{1p} } \\ {y_{1} = 0,} & {\text{otherwise }} \\ \end{array} } \right. \hfill \\ \left\{ {\begin{array}{*{20}c} {y_{2} = \beta_{2p} ,} & {{\text{if }}\beta_{2(p - 1)} { < }\left\lceil {{0}{\text{.7}} \times h_{2} } \right\rceil \le \beta_{2p} } \\ {y_{2} = 0,} & {{\text{otherwise}}} \\ \end{array} } \right. \hfill \\ \, \vdots \hfill \\ \left\{ {\begin{array}{*{20}c} {y_{8} = \beta_{8p} ,} & {{\text{if }}\beta_{8(p - 1)} < \left\lceil {{0}{\text{.7}} \times h_{2} { + 0}{\text{.7}} \times h_{4} + {0}{\text{.7}} \times h_{6} } \right\rceil \le \beta_{8p} } \\ {y_{8} = 0,} & {{\text{otherwise}}} \\ \end{array} } \right. \hfill \\ \end{gathered} $$

Then, a total of 11 MCVs candidates are shown in the second column of Table 4.

Step 5 Executing the comparison process and removing the non-minimal ones from those Y of step 4 to obtain all MCVs. After executing, a total of 11 MCVs are obtained.

Step 6 According to a total of 11 MCVs obtained from step 5, the reliability R5,5600,0.75 = \(\Pr \left\{ {\bigcup\nolimits_{i = 1}^{{{11}}} {\left\{ {Y|Y \ge Y_{i} } \right\}} } \right\}\) = 0.9650 is calculated by using the RSDP with ordering.

Under the requirements that the budget must be less than or equal 5600 and the supplier sustainability level must be greater than or equal 0.75, the possibility that the current supply chain can meet the five-unit demand of customer is 0.965. We further focus on the order allocations that we find in Step 1 and separately calculate the possibility that it can satisfy the demand and the budget. According to its flow vectors, the separate possibility is computed by executing steps 3 to 6. The separate possibilities that it can satisfy the demand and the budget of each order allocation are listed in Table 5. Under the goal of the supplier sustainability level of 0.75, we can choose order allocation (3, 2, 0) as a more appropriate one.

Table 5 The separate possibility of each order allocation
Full size table

4.2 Sensitivity analysis

We test the impact on the reliability for several budgets ranging from 5400 to 6100 with an increment of 100. The reliabilities under different budgets are shown in Fig. 3. The reliability substantially increases (from 0.79 to 0.94) when the budget adds from 5,400 to 5,500. However, continuing to increase the budget does not increase the reliability greatly. When the DMs expect the system reliability to reach 0.96, the best budget is 5,600. With a higher value of C = 6,100, the reliability increases to 0.97.

Fig. 3
figure 3

The reliabilities under different budgets

Full size image

Moreover, we test the impact on the reliability for several supplier sustainability levels ranging from 0.5 to 0.85 with an increment of 0.05. The reliabilities under different supplier sustainability levels are summarized in Fig. 4. Without considering the budget, when the reliability is required to reach 0.9, the supplier sustainability level can be maintained at 0.8. Lower budgets and higher supplier sustainability level lead to decreased reliability. According to the changes in reliability under different budgets or supplier sustainability levels, the managers can adjust appropriate decisions.

Fig. 4
figure 4

The reliabilities under different supplier sustainability levels

Full size image

4.3 Computational time analysis

To examine the efficiency of the proposed algorithm, the numerical experiments were performed for the SSCN shown in Fig. 2. The demand is 5, 10, 15, 20, and 25. For each case, each arc has capacities of 0, 5, 10, 15, 20, 25 and 30 with the corresponding probabilities 0.01, 0.01, 0.01, 0.01, 0.03, 0.03 and 0.90. The CPU time for run the proposed algorithm which is programmed by Python for the experiments with different demand is listed in Table 6. The execution time is recorded by three parts: Steps 1 to 3 is for feasible flow vectors generation, Steps 4 to 5 is for obtaining MCV and Step 6 is for reliability calculation. The program is executed on a personal computer with 3.6 GHz CPU (Intel Core i7-11700), 16 GB RAM, and Windows 11. The case for most complex demand requires at most 0.7 s to execute the proposed algorithm. It means that the proposed algorithm can evaluate reliability in an efficient way.

Table 6 CPU time for the proposed algorithm
Full size table

5 Conclusions

With sustainable suppliers necessary for various industries to achieve the sustainability of their supply chains and the multiple state of the carriers’ available carrying capacity, this research constructs an SSCN and proposes an algorithm to evaluate the comprehensive index, named reliability, under the consideration of supplier sustainability, budget, and supplier production capacity. Furthermore, this study provides the appropriate order allocations to managers in the circumstances described above. A numerical example demonstrates the utility of the proposed algorithm. In the numerical example, the reliability R5,5600,0.75 is 0.9650 under the five compatible order allocations. Additionally, according to the screened results, the possibility that each order allocation can meet the demand can be individual calculated, it can further help the managers to figure out the appropriate order allocation. The managers can decide on the supplier sustainability level, budget and evaluation strategy. The contributions of this research are summarized as follows:

  1. (1)

    The sustainable supply chain can be modeled as SSCN and the available delivery containers of the carrier above the arc is regarded as stochastic.

  2. (2)

    Reliability can be calculated in terms of all MCVs by the RSDP with ordering. This research provides the managers with a quantitative indicator to easily evaluate supply chain ability under considering the supplier sustainability, supplier production capacity, and budget.

  3. (3)

    According to the different supplier sustainability levels and the budget resulting in different probabilities of successful transportation, the more appropriate order allocation can be provided for the managers.

Nonetheless, specific concerns need to be tackled in future research. The proposed algorithm focuses on involving supplier sustainability into reliability evaluation problems. The prevalence of diverse products, materials, and customers within the supply chain is common, and reliability evaluation is worthy of study. In addition, the proposed algorithm is based on the more intuitive concept of MP. Another concept of minimal cut, commonly used to calculate reliability, can be adopted to solve this problem. Literature does not address the concept of minimal cut into the supply chain with supplier sustainability from the reliability perspective. Future research can be conducted based on the above to fill the gap in reliability evaluation problems with supplier sustainability.