Curves that allow the motion of a regular polygon

Abstract

This paper characterizes curves where a regular polygon of either a variable side length or a constant side length is allowed to rotate during k full revolutions while having its vertices on the curve during the motion. A constructive method to generate these curves is given based on the curve described by the polygon centers (centroids) during the motion and some examples are shown. Moreover, if the regular polygon divides the curve perimeter into parts of equal length, it is proved that the curve is either a rotational symmetric curve in the case of a variable side length or a circle otherwise. Finally, in the case of a regular polygon of constant side length rotating along a curve, a simple relation between the algebraic areas of such a curve and the curve of polygon centers is revisited.

1 Introduction

This paper is devoted to a geometrical question: how to characterize planar curves that allow the motion of a n-sided regular polygon of constant side length having its vertices on the curve and making k full revolutions?

The circle is the most obvious example of a curve where a regular polygon (in fact, any regular polygon) can move with its vertices always lying on it during the motion. The existence of curves different from the circle with such a property is well known and there are some papers providing partial constructions and examples of these curves, both in the convex case [2, 8, 13] and in the non-convex case [19,20,21].

An answer to the question can be provided from the results presented in the German paper [18], where different movement processes to generate trajectories described by the motion of a moving plane over a fixed one are studied. The methods used belong to classical kinematics.

The same question can also be partially answered from the works of Goldberg [5,6,7], based on a result of Meissner [16] that characterizes rotors in regular polygons. A rotor in a regular polygon is defined as a closed convex curve that can be rotated inside the regular polygon while always touching its sides during a complete rotation of the curve. Meissner showed that all the rotors in a n-sided regular polygon are given analytically by support functions

$$\begin{aligned} p(t) = a_0 + \sum _{k=1}^{\infty }\bigl (a_k\cos (k\,t)+b_k\sin (k\,t)\bigr ) \end{aligned}$$

such that

$$\begin{aligned} a_k = b_k = 0\quad \text {for}\quad k\ne \pm 1 \text { (mod }n\text {).} \end{aligned}$$

Support functions are widely used in convex geometry, the interested reader can find an introduction in [15].

Rotors constitute a generalization of curves of constant width. These can be seen as rotors in a square. Some other related works on rotors are [3, 4, 10, 14].

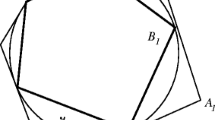
Goldberg states that for each convex rotor in a n-sided polygon, by maintaining the rotor fixed and rotating the regular polygon about it, the polygon vertices generate a curve with the desired property (i.e., where a regular polygon can rotate along). However, while this is true, there is no guarantee that the curve which is obtained is convex (see an example in Fig. 1).

Fig. 1

A rotor $\beta$ in a pentagon and a non-convex curve $\alpha$ generated by the motion of the vertices of the pentagon if it is slided along $\beta$

In this paper, a direct and simple way to characterize these curves without using rotors nor plane over plane movements is presented. In fact, we will consider a more general class of curves: those that allow the rotation of a n-sided regular polygon of a variable side length during k full revolutions while having their vertices always lying on the curve (Sect. 2). First, we provide a new characterization of these curves in Theorem 1 and some examples are shown. The idea is to start from the curve of polygon centers, i.e., the locus of the centers (centroids) of the regular polygon during its motion. The chosen parameterization of the curve of polygon centers will be relevant for the shape of the resulting curve.

In Theorem 2 we prove that if in one of these curves the n-sided regular polygon divides the curve perimeter into equal parts, then the curve has rotational symmetry of an angle $\frac{2\pi }{n}$.

We then focus on the case where the n-sided regular polygon has constant side length during the entire motion (Sect. 3). As a direct consequence of Theorem 1 we also have a characterization of these curves (Theorem 3), which is essentially one of the results that can be deduced from [18]. In the particular case where the curve of polygon centers is a circle parameterized by the arc-length, we get the construction of generalized polygonal Wankel engines given in [17] (see also the examples from [18]). This will be seen in detail in Example 3.

The characterization provides a constructive way to generate these curves as parametric curves. In particular, we are able to prove explicitly the existence of convex bodies with an equichordal convex body in their interior (Example 5) by a computation of the curvature function.

We show in Theorem 4 that the circle is the unique curve where a n-sided regular polygon of constant side length, with $n>2$, can rotate along while dividing the curve perimeter into parts of equal length. Although related, this result must not be confused with similar problems where equilateral polygons (which are not necessarily regular) are considered, such as Ulam’s problem 19 from the Scottish book [1, 24] or the kind of problems considered by Salkowski [23, 25].

Finally, given a curve $\alpha$ where a regular polygon of a constant side length can rotate, a relation between the algebraic areas of $\alpha$ and the corresponding curve of polygon centers is obtained in Theorem 5 by using a classical theorem in kinematics due to Leudesdorf. We must point out that the same result can also be found in [18], but derived differently using a J. Steiner formula and the Steiner point.

2 A characterization of curves where a regular polygon can rotate

We say that a regular polygon is allowed to move with an always-forward motion over a closed curve if its vertices can move along the curve such that the polygon is always rotating in a strictly monotonous way (i.e., the angle of rotation of the polygon can be seen as a strictly monotonous function of time).

In the following result we characterize curves where regular polygons (of a possibly variable size) can rotate along with an always-forward motion.

Theorem 1

Let $n\in {\mathbb {N}}$, $n>2$, and $k\in {\mathbb {Z}}\setminus \{0\}$ such that $\gcd (k,n)=1$. Any closed curve where an always-forward motion of a regular polygon of n sides of variable length is allowed and that makes k full revolutions can be parameterized as $\alpha :\mathopen {}\left[ 0,2\pi k\right] \mathclose {}\rightarrow {\mathbb {R}}^2$ by

$$\begin{aligned} \alpha (t) = c(t) + a(t)\,(\cos t,\,\sin t), \end{aligned}$$

where $a:\mathopen {}\left[ 0,2\pi k\right] \mathclose {}\rightarrow \mathopen {}\left]0,+\infty \right[\mathclose {}$ is extendable to a $\frac{2\pi k}{n}$-periodic function in ${\mathbb {R}}$ with minimum period $\frac{2\pi k}{n}$ and $c:\mathopen {}\left[ 0,2\pi k\right] \mathclose {}\rightarrow {\mathbb {R}}^2$ is a closed parametric curve with minimum period $\frac{2\pi k}{n}$, regarded as the curve of polygon centers of $\alpha$.

Proof

Let $\alpha : I\rightarrow {\mathbb {R}}^2$, where I is some closed interval, be a (single-traced) closed parametric curve where a regular n-sided polygon $\Gamma (t)$ of side length $\ell (t)>0$ can move along with an always-forward movement during k revolutions. Consider $\alpha$, as a closed curve, being continuously extendable to ${\mathbb {R}}$ by periodicity.

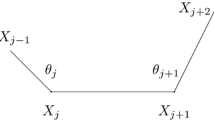
By hypothesis, there exists a homeomorphism $f:{\mathbb {R}}\rightarrow {\mathbb {R}}$ such that if $\alpha (t)$ is a vertex of the regular polygon $\Gamma (t)$, then $\alpha \bigl (f(t)\bigr )$ is the next vertex of $\Gamma (t)$ according to the parameterization of $\alpha$.

Define $f^{i} = f\circ {\mathop {\cdots }\limits ^{i)}} \circ f$. We have

$$\begin{aligned} \Bigl \Vert \alpha \bigl (f^{i+1}(t)\bigr )-\alpha \bigl (f^{i}(t)\bigr )\Bigr \Vert = \ell (t), \end{aligned}$$

for all $t\in I$, and $\alpha \bigl (f^{n}(t)\bigr ) = \alpha (t)$. Notice that the last condition needs that $n>2$. The curve C of polygon centers of $\alpha$ can be parameterized by

$$\begin{aligned} c(t){:}{=}\frac{1}{n}\sum _{i=1}^n\alpha \bigl (f^{i}(t)\bigr ). \end{aligned}$$

By the definition, notice that $c\bigl (f(t)\bigr ) = c(t)$ for all $t\in I$.

Define $\textbf{v}:{\mathbb {R}}\rightarrow {\mathbb {R}}^2$ as the continuous function such that, for each c(t), $\textbf{v}(t)$ gives a unit direction for which the vertex $\alpha (t)$ is found from c(t). Let $a:{\mathbb {R}}\rightarrow \mathopen {}\left]0,+\infty \right[\mathclose {}$ be the distance from c(t) to $\alpha (t)$, i.e.

$$\begin{aligned} a(t) = \bigl \Vert \alpha (t)-c(t)\bigr \Vert . \end{aligned}$$

Thus, we can write

$$\begin{aligned} \alpha (t) = c(t) + a(t)\,\textbf{v}(t). \end{aligned}$$

(1)

Notice that since $c(t) = c\bigl (f(t)\bigr )$ for all $t\in I$ and $\Gamma (t)$ is a regular polygon, we have that $a(t) = a\bigl (f(t)\bigr )$ for all $t\in I$.

The function $\textbf{v}|_{I}:I\rightarrow {\mathbb {R}}^2$ can be seen as a parameterization of a k-times traced unit circle that describes the position of a resized version of the regular polygon $\Gamma (t)$ for each $t\in I$. Indeed, since $c\bigl (f(t)\bigr ) = c(t)$ and $a\bigl (f(t)\bigr ) = a(t)$, we have

$$\begin{aligned} \alpha \bigl (f(t)\bigr ) = c(t) +a(t)\,\textbf{v}\bigl (f(t)\bigr ). \end{aligned}$$

(2)

From (1) and (2), we deduce

$$\begin{aligned} a(t)\,\Bigl (\textbf{v}\bigl (f(t)\bigr )-\textbf{v}(t)\Bigr ) = \alpha \bigl (f(t)\bigr )-\alpha (t). \end{aligned}$$

Thus,

$$\begin{aligned} \Bigl \Vert \textbf{v}\bigl (f(t)\bigr )-\textbf{v}(t)\Bigr \Vert = \frac{\ell (t)}{a(t)} \end{aligned}$$

is constant, because $\Gamma (t)$ is a regular polygon. Moreover, from the expression

$$\begin{aligned} \textbf{v}(t) = \frac{1}{a(t)}\,\bigl (\alpha (t)-c(t)\bigr ) \end{aligned}$$

and since $c\bigl (f^{i}(t)\bigr ) = c(t)$, we have that

$$\begin{aligned} \Bigl \langle \textbf{v}\bigl (f^{i+1}(t)\bigr )&-\textbf{v}\bigl (f^{i}(t)\bigr ),\,\textbf{v}\bigl (f^{i}(t)\bigr )-\textbf{v}\bigl (f^{i-1}(t)\bigr )\Bigr \rangle \\&= \frac{1}{a(t)^2}\,\Bigl \langle \alpha \bigl (f^{i+1}(t)\bigr )-\alpha \bigl (f^{i}(t)\bigr ),\,\alpha \bigl (f^{i}(t)\bigr )-\alpha \bigl (f^{i-1}(t)\bigr )\Bigr \rangle \end{aligned}$$

is also constant, because $\ell (t)/a(t)$ is constant and $\alpha \bigl (f^{i}(t)\bigr )$ are the vertices of an equiangular polygon. Therefore, the points $\textbf{v}\bigl (f^{i}(t)\bigr )$ also describe the vertices of an equiangular polygon and so, of a n-sided regular polygon of constant side length $\ell (t)/a(t)$.

Since the regular polygon must rotate in a strictly monotonous way during k revolutions, we have that $\textbf{v}|_{I}:I\rightarrow {\mathbb {R}}^2$ can be written as

$$\begin{aligned} \textbf{v}|_{I}(t) = \bigl (\cos g(t),\,\sin g(t)\bigr ), \end{aligned}$$

where $g:I\rightarrow \mathopen {}\left[ 0,2\pi k\right] \mathclose {}$ is a homeomorphism (i.e., the function g describes a parameterization of the unit circle $\textbf{v}$ that may result in a motion of a regular polygon with non-constant velocity).

Consider a reparameterization through $g^{-1}:\mathopen {}\left[ 0,2\pi k\right] \mathclose {}\rightarrow I$, so that

$$\begin{aligned} \tilde{\textbf{v}}(t) = (\textbf{v}\circ g^{-1})(t) = \bigl (\cos t,\,\sin t),\end{aligned}$$

(3)

for $t\in \mathopen {}\left[ 0,2\pi k\right] \mathclose {}$.

Define also ${\tilde{c}}=c\circ g^{-1}$, ${\tilde{\alpha }} = \alpha \circ g^{-1}$, ${\tilde{a}}=a\circ g^{-1}$ and ${\tilde{f}} = g \circ f\circ g^{-1}$. This way, we have the same properties for the new parameterizations. First, we have that

$$\begin{aligned} \Bigl \Vert \tilde{\textbf{v}}\bigl ({\tilde{f}}(t)\bigr )-\tilde{\textbf{v}}(t)\Bigr \Vert = \frac{\ell \bigl (g^{-1}(t)\bigr )}{a\bigl (g^{-1}(t)\bigr )}=\frac{\ell (t)}{a(t)} \end{aligned}$$

(4)

is contant. Since ${\tilde{f}}^{i}=g\circ f^{i}\circ g^{-1}$, we also have that the curve of polygon centers is

$$\begin{aligned} {\tilde{c}}(t) = \frac{1}{n}\,\sum _{i=1}^{n}{\tilde{\alpha }}\bigl ({\tilde{f}}^{i}(t)\bigr ) \end{aligned}$$

and is such that ${\tilde{c}}\bigl ({\tilde{f}}(t)\bigr )={\tilde{c}}(t).$ Analogously, ${\tilde{a}}\bigl ({\tilde{f}}(t)\bigr )={\tilde{a}}(t)$. Finally, we indeed get ${\tilde{\alpha }}:\mathopen {}\left[ 0,2\pi k\right] \mathclose {}\rightarrow {\mathbb {R}}^2$ given by

$$\begin{aligned} {\tilde{\alpha }}(t) = {\tilde{c}}(t) + a\,\tilde{\textbf{v}}(t), \end{aligned}$$

as in the statement.

Now, from (4) using the expression (3) we get

$$\begin{aligned} 2\,\Bigl (1-\cos \bigl (t-{\tilde{f}}(t)\bigr )\Bigr ) = \frac{\ell ^2(t)}{a^2(t)}. \end{aligned}$$

(5)

By the cosine rule,

$$\begin{aligned} \frac{\ell ^2(t)}{a^2(t)} = 2\,(1-\cos \theta ), \end{aligned}$$

(6)

where $\theta = \frac{2\pi j}{n}$, for some $j\in {\mathbb {Z}}$ such that $|j|<|k|\,n$ and $\gcd (j,n)=1$. The need of this integer j is the following: given $\alpha (t)$, the next vertex $\alpha \bigl (f(t)\bigr )$ according to the parameterization of $\alpha$ is not necessarily the vertex of the polygon that provides a convex polygon, that is, $\Gamma (t)$ can be a star polygon (see Fig. 2).

Fig. 2

The unit circle $\tilde{\textbf{v}}$ and an inscribed regular polygon. The value of $\theta$ determines if the polygon is convex or star

Now, with (5) and (6) we deduce that

$$\begin{aligned} {\tilde{f}}(t) = t \pm \frac{2\pi j}{n}. \end{aligned}$$

(7)

As a consequence, we have that ${\tilde{c}}$ and ${\tilde{a}}$ are $\frac{2\pi j}{n}$-periodic. Moreover, the period $\frac{2\pi j}{n}$ is the minimum period by definition of ${\tilde{f}}$, that provides the next vertex of the regular polygon according to the parameterization of ${\tilde{\alpha }}$.

Moreover, since ${\tilde{f}}$ is defined such that given a vertex ${\tilde{\alpha }}(t)$ of the regular polygon, $\alpha \bigl ({\tilde{f}}(t)\bigr )$ provides the next vertex according to the parameterization of ${\tilde{\alpha }}$ and ${\tilde{\alpha }}$ is single-traced in $\mathopen {}\left[ 0,2\pi k\right] \mathclose {}$, we necessarily have ${\tilde{f}}^n(t) = t+2\pi k$. So, from the expression (7) we conclude that $j=k$. $\square$

Remark 1

The function g from the proof of Theorem 3 indicates the rotation velocity of the regular polygon with respect to the curve of polygon centers C. Notice that the reparameterization we have done in order to have a constant velocity in the rotation of the regular polygon is not restrictive, because such a velocity can also be controlled by the chosen parameterization c of C. In other words, a change of the rotation velocity of the regular polygon is transferred to a different parameterization of the curve of polygon centers.

Analogously, a different position of the regular polygon at the starting point of c, which corresponds to a parameterization $\tilde{\textbf{v}}$ starting at a point different to (1, 0), can also be determined by an appropriate reparameterization of the curve of polygon centers.

In particular, a choice of a reverse parameterization of C leads generally to a different curve described by $\alpha$.

Notice that we understand “reparameterization” in a broad sense, simply as a continuous change of variables; we do not require differentiability nor injectivity.

From Theorem 1 and its proof, we can provide a method to construct our curves.

Algorithm 1

Construction of a curve for which a regular polygon of n sides with a variable length can move along with an always-forward motion and making k full revolutions:  

• 1. Choose the number of vertices $n\in {\mathbb {N}}$, $n>2$, of the regular polygon and the number of full revolutions $k\in {\mathbb {Z}}\setminus \{0\}$ that it will perform.

• 2. Choose a closed parametric curve $c:\mathopen {}\left[ 0,2\pi k\right] \mathclose {}\rightarrow {\mathbb {R}}^2$, with minimum period $2\pi k$, which will serve as the curve of polygon centers. The chosen parameterization is very relevant.

• 3. Choose a $2\pi k$-periodic function $a:\mathopen {}\left[ 0,2\pi k\right] \mathclose {}\rightarrow \mathopen {}\left]0,+\infty \right[\mathclose {}$, with minimum period $2\pi k$. The function a controls the size of the regular polygon during the motion.

• 4. Construct the desired curve as $\alpha _{n,k}:\mathopen {}\left[ 0,2\pi k\right] \mathclose {}\rightarrow {\mathbb {R}}^2$ given by

  $$\begin{aligned} \alpha _{n,k}(t) = c(n\,t) + a(n\,t)\,(\cos t,\,\sin t). \end{aligned}$$

• 5. The regular polygon of vertices $\alpha \bigl (f^{i}(t)\bigr )$, $i=0,1,\ldots n-1$, can be constructed with

  $$\begin{aligned} f(t) = t+\frac{2\pi kj}{n}, \end{aligned}$$

  with $j\in {\mathbb {N}}$ such that $j<\frac{n}{2}$ and $\gcd (n,j)=1$. The choice of j will determine if we get either a convex or some star polygon.

Example 1

Algorithm 1 gives an infinite number of possibilities for constructing curves where a regular polygon of variable side length can rotate during k full revolutions.

As an example, given $k\in {\mathbb {Z}}\setminus \{0\}$, consider a parametric circle

$$\begin{aligned} c(t) = \mathopen {}\left( \cos \mathopen {}\left( \frac{t}{k}\right) \mathclose {},\,\sin \mathopen {}\left( \frac{t}{k}\right) \mathclose {}\right) \mathclose {},\quad t\in \mathopen {}\left[ 0,2\pi k\right] \mathclose {}, \end{aligned}$$

as the curve of polygon centers, and let $a:\mathopen {}\left[ 0,2\pi k\right] \mathclose {}\rightarrow \mathopen {}\left]0,+\infty \right[\mathclose {}$ be the $2\pi k$-periodic function

$$\begin{aligned} a(t) = 3+\sin \mathopen {}\left( \frac{t}{k}\right) \mathclose {}. \end{aligned}$$

We can thus construct the curve $\alpha _{n,k}$ as in Algorithm 1, see some examples in Fig. 3.

Fig. 3

Some examples $\alpha _{n,k}$. From left to right: $n=3$, $k=1$; $n=4$, $k=1$; and $n=3$, $k=2$

Of course, the same procedure can be easily repeated for a different parameterization of the unit circle or taking any other parametric curve as the curve of polygon centers.

Theorem 2

Let $n\in {\mathbb {N}}$, $n>2$, and $k\in {\mathbb {Z}}\setminus \{0\}$ such that $\gcd (k,n)=1$. If $\alpha$ is a $\mathcal {C}^1$-curve where a n-sided regular polygon, of a side length given by a $\mathcal {C}^1$-function, can rotate with an always-forward motion during k full revolutions and such that the vertices of the polygon divide the perimeter of $\alpha$ into equal parts, then $\alpha$ has rotational symmetry of an angle $\frac{2\pi }{n}$.

Proof

By Theorem 1 we have that

$$\begin{aligned} \alpha (t) = c(n\,t)+a(t)\,(\cos t,\,\sin t), \end{aligned}$$

where c is a closed curve in $\mathopen {}\left[ 0,2\pi k\right] \mathclose {}$, with $2\pi k$ being the minimum period and a is a $\mathcal {C}^1$-function that is $\frac{2\pi k}{n}$-periodic and such that $a(t)>0$ for all $t\in \mathopen {}\left[ 0,2\pi k\right] \mathclose {}$. Thus,

$$\begin{aligned} \alpha '(t) = n\,c'(n\,t)+a'(t)\,(\cos t,\,\sin t) + a(t)\,(-\sin t,\,\cos t), \end{aligned}$$

so that

$$\begin{aligned} \bigl \Vert \alpha '(t)\bigr \Vert ^2 = n^2\,\bigl \Vert c'(n\,t)\bigr \Vert ^2&+ a'(t)^2+a(t)^2\\&+2\,n\,a'(t)\,\bigl \langle c'(n\,t),\,(\cos t,\,\sin t)\bigr \rangle \\&+ 2\,n\,a(t)\,\bigl \langle c'(n\,t),\,(-\sin t,\,\cos t)\bigr \rangle . \end{aligned}$$

Since the regular polygon divides the perimeter of $\alpha$ into parts of equal length, we have that $\Vert \alpha '\Vert$ must be a $\frac{2\pi k}{n}$-periodic function. Indeed, we have

$$\begin{aligned} F(t) = \int _{t}^{t+\frac{2\pi k}{n}}\bigl \Vert \alpha '(s)\bigr \Vert \;\text {d}{s} \end{aligned}$$

is constant for all $t\in \mathopen {}\left[ 0,2\pi k\right] \mathclose {}$. Differentiating this expression, we deduce that

$$\begin{aligned} \bigl \Vert \alpha '(t)\bigr \Vert =\mathopen {}\left\| \alpha '\mathopen {}\left( t+\frac{2\pi k}{n}\right) \mathclose {}\right\| \mathclose {}, \end{aligned}$$

for all $t\in \mathopen {}\left[ 0,2\pi k\right] \mathclose {}$.

Therefore, we deduce that

$$\begin{aligned} a'(t)\,\bigl \langle c'(n\,t),\,(\cos t,\,\sin t)\bigr \rangle +a(t)\,\bigl \langle c'(n\,t),\,(-\sin t,\,\cos t)\bigr \rangle \end{aligned}$$

must be $\frac{2\pi k}{n}$-periodic. If $c(t) = \bigl (x(t),\,y(t)\bigr )$, the expression above can be written as

$$\begin{aligned} \bigl (-a(t)\sin t+a'(t)\cos t\bigr )\,x'(n\,t) + \bigl (a(t)\cos t + a'(t)\sin t\bigr )\,y'(n\,t). \end{aligned}$$

Since a and $a'$ are $\frac{2\pi k}{n}$-periodic and $x'$ and $y'$ are $2\pi k$-periodic, the previous function is $\frac{2\pi k}{n}$-periodic if and only if

$$\begin{aligned} 2\sin \mathopen {}\left( \frac{k\,\pi }{n}\right) \mathclose {}&\, \Biggl [\biggl (a(t)\cos \mathopen {}\left( t+\frac{k\,\pi }{n}\right) \mathclose {} +a'(t)\sin \mathopen {}\left( t+\frac{k\,\pi }{n}\right) \mathclose {}\biggr )\,x'(n\,t)\\&+\biggl (a(t)\sin \mathopen {}\left( t+\frac{k\,\pi }{n}\right) \mathclose {} -a'(t)\,\cos \mathopen {}\left( t+\frac{k\,\pi }{n}\right) \mathclose {}\biggr )\,y'(n\,t)\Biggr ]\mathclose {}=0. \end{aligned}$$

Since $n>2$ and $\gcd (k,n)=1$, this holds if and only if

$$\begin{aligned} \biggl (&a(t)\cos \mathopen {}\left( t+\frac{k\,\pi }{n}\right) \mathclose {} +a'(t)\sin \mathopen {}\left( t+\frac{k\,\pi }{n}\right) \mathclose {}\biggr )\,x'(n\,t)\nonumber \\&+\biggl (a(t)\sin \mathopen {}\left( t+\frac{k\,\pi }{n}\right) \mathclose {} -a'(t)\,\cos \mathopen {}\left( t+\frac{k\,\pi }{n}\right) \mathclose {}\biggr )\,y'(n\,t)=0. \end{aligned}$$

(8)

Moreover, evaluating (8) at $t+\frac{2\pi k}{n}$, we also have

$$\begin{aligned} \biggl (&a(t)\cos \mathopen {}\left( t+\frac{3\,k\,\pi }{n}\right) \mathclose {}+a'(t)\sin \mathopen {} \left( t+\frac{3\,k\,\pi }{n}\right) \mathclose {}\biggr )\,x'(n\,t)\nonumber \\&+\biggl (a(t)\sin \mathopen {}\left( t+\frac{3\,k\,\pi }{n}\right) \mathclose {}-a'(t)\, \cos \mathopen {}\left( t+\frac{3\,k\,\pi }{n}\right) \mathclose {}\biggr )\,y'(n\,t)=0. \end{aligned}$$

(9)

We can see Eqs. (8) and (9) forming a system of equations with unknowns $x'(n\,t)$ and $y'(n\,t)$. The determinant of the matrix A of this system of equations is

$$\begin{aligned} |A|=\sin \mathopen {}\left( \frac{2\pi k}{n}\right) \mathclose {}\,\bigl (a(t)^2+a'(t)^2\bigr ), \end{aligned}$$

which is non-zero if $n>2$. In such a case, the unique solution of the system is $x'(n\,t) = y'(n\,t) = 0$, which produces a degenerated curve of polygon centers reduced to a point. Therefore the regular polygon is rotating through this point with a size according to the $\frac{2\pi k}{n}$-periodic function a. This implies that $\alpha$ has rotational symmetry of an angle $\frac{2\pi k}{n}$. Since the domain of $\alpha$ is $\mathopen {}\left[ 0,2\pi k\right] \mathclose {}$ this implies that $\alpha$ has rotational symmetry of an angle $\frac{2\pi }{n}$. $\square$

Example 2

Let us illustrate Theorem 2 with some examples. Suppose that the curve of polygon centers is $c(t) = (0,0)$, a point. Given $k\in {\mathbb {Z}}\setminus \{0\}$, Consider the function $a:\mathopen {}\left[ 0,2\pi k\right] \mathclose {}\rightarrow \mathopen {}\left]0,+\infty \right[\mathclose {}$ defined by

$$\begin{aligned} a(t) = 2+\sin \mathopen {}\left( \frac{t}{k}\right) \mathclose {}, \end{aligned}$$

which is $\frac{2\pi k}{n}$-periodic. Thus, the curves $\alpha _{n,k}$ found by Theorem 1 are curves that have rotational symmetry of an angle $\frac{2\pi }{n}$. See some examples in Fig. 4 for different number k of revolutions.

Fig. 4

Curves where a regular polygon of variable side length rotate during k revolutions and which have rotational symmetry of an angle $\frac{2\pi }{n}$, for $n=5$ and different values of k

3 Curves where regular polygons of constant side length can rotate

As a direct consequence of Theorem 1 we directly obtain the following result by taking $a(t) = a$ constant.

Theorem 3

Let $n\in {\mathbb {N}}$, $n>2$, and $k\in {\mathbb {Z}}\setminus \{0\}$ such that $\gcd (k,n)=1$. Any closed curve where an always-forward motion of a regular polygon of n sides of constant length is allowed and that makes k full revolutions can be parameterized as $\alpha :\mathopen {}\left[ 0,2\pi k\right] \mathclose {}\rightarrow {\mathbb {R}}^2$ by

$$\begin{aligned} \alpha (t) = c(t) + a\,(\cos t,\,\sin t), \end{aligned}$$

where $a>0$ and $c:\mathopen {}\left[ 0,2\pi k\right] \mathclose {}\rightarrow {\mathbb {R}}^2$ is a closed parametric curve with minimum period $\frac{2\pi k}{n}$, regarded as the curve of polygon centers of $\alpha$.

As it has been already remarked, Theorem 3 can also be deduced from the results of [18], where a different kinematics approach via movements is followed.

Now we are going to use Algorithm 1 taking $a(t) = a$ constant to contruct examples of this kind of curves.

Example 3

Consider an arc-length parameterized unit circle given by $c(t) = (\cos t,\,\sin t)$. The generated curve is

$$\begin{aligned} \alpha _{n,k,a}(t) = \bigl (a\cos (t)+\cos (n\,t),\, a\sin (t)+\sin (n\,t)\bigr ), \quad t\in \mathopen {}\left[ 0,2\pi k\right] \mathclose {}, \end{aligned}$$

where $a>0$ and $n\in {\mathbb {N}}$, $n>2$. Consider the case where the regular polygon makes just a full revolution, that is, $k=1$. These curves are generalized polygonal Wankel engines according to [17] (see also [18]). Some generated curves by varying the value of the free parameter $a>0$ are plotted in Fig. 5.

Fig. 5

A family of curves $\alpha _{3,1,a}$, for different values of $a>0$, where a regular triangle can travel along having an arc-length parameterized unit circle as its curve of polygon centers

We have

$$\begin{aligned} \bigl \Vert \alpha _{n,1,a}'(t)\bigr \Vert = a^2+n^2+2\,a\,n\cos (t-n\,t). \end{aligned}$$

It is easy to check that this expression equal to zero has real solutions if and only if $a=n$. Thus, given any $n\in {\mathbb {N}}$, $n>2$, the curve $\alpha _{n,1,a}$ is regular for all $a\ne n$.

The curvature function of $\alpha _{n,1,a}$ is

$$\begin{aligned} \kappa _{\alpha }(t) = \frac{a^2+a\,(n+1)\,n\cos (t-n\,t)+n^3}{\left( a^2+2 \,a\,n \cos (t-n\,t)+n^2\right) ^{3/2}}. \end{aligned}$$

If $a\le n$ or $a\ge n^2$ then

$$\begin{aligned} a^2-a\,(n+1)\,n+n^3\ge 0 \end{aligned}$$

and we have that $\kappa _{\alpha }(t)\ge 0$ for all $t\in \mathopen {}\left[ 0,2\pi \right] \mathclose {}$. The case $a\le n$ corresponds to non-simple shapes which are rosettes. The case $a\ge n^2$ yields convex curves. In each case, the rotation index of these curves can be checked out by computing a continuous primitive of $\kappa _{\alpha }\Vert \alpha _{n,1,a}'\Vert$ and making the difference of its evaluation at the endpoints, namely $t=2\pi$ and $t=0$.

See in Fig. 6 the generated curve $\alpha _{n,1,a}$ for the first value of $a>0$ that yields a convex curve, which is $a=n^2$, shown for different regular polygons.

Fig. 6

The curves $\alpha _{n,1,n^2}$ for $n=3,4$ and 5, respectively. For any $a>n^2$, the curves $\alpha _{n,1,a}$ are strictly convex

The curve for $a=n$ (the only singular curve, which makes the transition between non-convex curves and rosettes) turns out to be $(\phi ,\ell )$-isochordal-viewed, where $\ell$ is the side length of the regular polygon (triangle) and $\phi = \frac{\pi }{n}$ (see an example in Fig. 7-middle). This means that the curve can be enveloped by a pair of lines making a constant angle $\phi$ and such that at each position of these lines, their contact points with the curve are a constant distance $\ell$ apart.

Indeed, if $\textbf{t}_{n,a}$ is the tangent vector of $\alpha _{n,1,a}$, where it can be defined, we can check that

$$\begin{aligned} \mathopen {}\left\langle \textbf{t}_{n,n}(t),\,\textbf{t}_{n,n}\mathopen {} \left( t+\frac{2\pi }{n}\right) \mathclose {}\right\rangle \mathclose {} =s(t)\cos \mathopen {}\left( \frac{\pi }{n}\right) \mathclose {}, \end{aligned}$$

where s(t) is a sign function, so that the angle between the tangent vectors to $\alpha _{n,1,a}$ defined by the chord of side length $\ell$ is either $\frac{\pi }{n}$ or $\pi -\frac{\pi }{n}$. Therefore, the angle between these tangent lines is $\frac{\pi }{n}$.

Fig. 7

The curves $\alpha _{n,1,a}$ for $n=3$ and different values of a. The curve for $a=n=3$ is $(\frac{\pi }{3},\sqrt{3}\,a)$-isochordal viewed

Example 4

Now we will show how the parameterization of the curve C of polygon centers is very relevant for the constructed curve. Notice that there is no constraint on the way we parameterize the curve as long as it is $2\pi$-periodic (i.e., the parameterization of C is not necessarily injective). See in Fig. 8 three examples of curves $\alpha _{n,1,a}$ for the following parameterizations of C:

$$\begin{aligned} c_1(t)&= \bigl (\cos (-t),\,\sin (-t)\bigr ),\\ c_2(t)&= \Bigl (\cos (t+\sin (t)\bigr ),\,\sin \bigl (t+\sin (t)\bigr )\Bigr ),\\ c_3(t)&= \Bigl (\cos (t+2\sin (3\,t)\bigr ),\,\sin \bigl (t+2\sin (3\,t)\bigr )\Bigr ). \end{aligned}$$

Fig. 8

The curves $\alpha _{n,1,a}$ for $n=3$, $a=9$ and different parameterizations $c_i$ of the unit circle, $i=1,2,3$

In particular, as seen for $c_1$, a reversal of the orientation of the parameterization produces, in general, a different curve.

Example 5

Consider an ellipse parameterized by $c(t) = (2\cos t,\,\sin t)$ and $k=1$. The generated curve is

$$\begin{aligned} \alpha _{n,a}(t) = \bigl (a\cos (t)+2\cos (n\,t),\, a\sin (t)+\sin (n\,t)\bigr ). \end{aligned}$$

See in Fig. 9 some generated curves by varying the value of the free parameter $a>0$.

Fig. 9

A family of curves $\alpha _{3,a}$, for different values of $a>0$, where a regular triangle can travel along having an ellipse as its curve of polygon centers

It can be easily proved that the curve $\alpha _{3,a}$ is convex and regular if $a>9$.

The parametric expression of the envelope $\varepsilon$ defined by the chords of constant length can be computed explicitly. In the case $n=3$, its curvature function can be written as

$$\begin{aligned} \kappa _{\varepsilon }(t)=\frac{2}{\mathopen {}\left| a-9\sin \mathopen {} \left( 2\,t+\frac{\pi }{6}\right) \mathclose {}-15\sin \mathopen {}\left( \frac{\pi }{6}-4\,t\right) \mathclose {}\right| \mathclose {}}, \end{aligned}$$

for $t\in \mathopen {}\left[ 0,2\pi \right] \mathclose {}$.

The function

$$\begin{aligned} f(t) = 9\sin \mathopen {}\left( 2\,t+\frac{\pi }{6}\right) \mathclose {} +15\sin \mathopen {}\left( \frac{\pi }{6}-4\,t\right) \mathclose {} \end{aligned}$$

has an absolute minimum value of $-24$ and an absolute maximum of $\frac{627}{40} = 15.675$ in $\mathopen {}\left[ 0,2\pi \right] \mathclose {}$. Therefore, the envelope is strictly convex (and regular) if and only if $a>\frac{627}{40}$. Notice that in this case, the curve $\alpha _{3,a}$ is convex as well. See in Fig. 10 some examples of these envelopes for different values of $a>0$.

Fig. 10

Some curves $\alpha _{3,a}$ with their associated envelopes of the chords of constant length for different values of $a>0$

Fig. 11

The generated parametric curve $\alpha _{3,1}$ has stationary points while a regular triangle rotates about it

Remember that a convex body L is said to be an equichordal body for a convex body K if $L\subset \text {int}\,K$ and every chord of K tangent to L has constant length. The authors of [9] raised the question if there exist convex bodies different from balls which possess an equichordal convex body in its interior. The interested reader can also see the paper [22] on the equichordal property.

From the construction of the envelope above, we have found an infinite number of explicit examples of convex bodies different from balls that have a equichordal convex body in its interior.

This construction can be repeated for any other integer $n>3$ providing even more examples of this kind of curves.

Remark 2

Notice that from Theorems 1 and 3 the curve of polygon centers c and the generated curve $\alpha$ are not necessarily simple. In particular, there could be segments of these curves which are multiple-traced when following the trajectory given by their parameterizations. Further, notice that the assumption of these statements on the always-forward motion (no stationary points) of the regular polygon is applied to the rotation of this polygon about its center. Nothing prevents that there could be stationary points for instance in the generated curve $\alpha$. In fact, if we consider the curve of polygon centers $c:\mathopen {}\left[ 0,2\pi \right] \mathclose {}\rightarrow {\mathbb {R}}^2$ parameterized by

$$\begin{aligned} c(t) = {\left\{ \begin{array}{ll} \bigl (\sin (\pi /6-t/3),\,\cos (\pi /6-t/3)\bigr ),\quad &{}\text {if }t<\pi ,\\ \bigl (-\cos (t/3),\,\sqrt{3}-\sin (t/3)\bigr ),\quad &{}\text {if } t\ge \pi ,\end{array}\right. } \end{aligned}$$

and extended by periodicity to ${\mathbb {R}}$, then the curve $\alpha _{n,a}$ that is found for $n=3$ and $a=1$ has stationary points, which is a classical example [8] of a curve where a regular triangle can rotate (see Fig. 11).

Now, using Theorem 2 we can directly get a characterization of the circle as follows.

Theorem 4

Let $n\in {\mathbb {N}}$, $n>2$, and $k\in {\mathbb {Z}}\setminus \{0\}$ such that $\gcd (k,n)=1$. If $\alpha$ is a $\mathcal {C}^1$-curve where a n-sided regular polygon of constant side length can rotate with an always-forward motion during k full revolutions and such that the vertices of the polygon divide the perimeter of $\alpha$ into equal parts, then $\alpha$ is a circle.

Proof

We known by Theorem 2 that $\alpha$ must have rotational symmetry of an angle $\frac{2\pi }{n}$ with a(t) being the function that determines the distance of each point of $\alpha$ to the center of symmetry. Since a(t) is constant in this case, we deduce that $\alpha$ is a (possibly multiple traced) circle. $\square$

Finally, we revisit an expression that relates the algebraic areas (counted by sign and multiplicity) of curves where a regular polygon of constant side length can rotate along and the corresponding curve of polygon centers (see Fig. 12). A proof of this formula is given in [18] using a J. Steiner result and the Steiner point. Instead, we will prove it as a consequence of a classical kinematics theorem by Leudesdorf [11, 12].

Fig. 12

An example showing the difference of areas of Theorem 5, for $k=1$

Theorem 5

Let $n\in {\mathbb {N}}$, $n>2$, and $k\in {\mathbb {Z}}\setminus \{0\}$ such that $\gcd (k,n)=1$. If $\alpha$ is a $\mathcal {C}^1$-curve where a n-sided regular polygon of constant side length is allowed to rotate with an always-forward motion during k full revolutions and c is the curve of polygon centers, then the algebraic areas of $\alpha$ and c are related through

$$\begin{aligned} \mathcal {A}(\alpha ) = \mathcal {A}(c) + \pi \,k\,a^2, \end{aligned}$$

where a is the circumradius of the regular polygon.

Proof

Consider the motion of a moving plane over another fixed one making k full revolutions. Let A, B, C and P be four fixed points on the moving plane that, during the motion, will describe four closed curves over the fixed plane. Leudesdorf’s theorem [11] states that the areas of these four curves are related through the relation

$$\begin{aligned} \mathcal {A}(P) = x\,\mathcal {A}(A) + y\,\mathcal {A}(B) + z\,\mathcal {A}(C) +\pi \,k\,T, \end{aligned}$$

where [x, y, z] are the barycentric coordinates of P referred to ABC as a triangle of reference ($x+y+z=1$) and T is the power of the point P to the circle rounding ABC.

In our case, let A, B and C be three vertices of the regular polygon and let P be the polygon center. Thus, since the three points describe the same curve $\alpha$ and so the same area, we have

$$\begin{aligned} \mathcal {A}(P) = \mathcal {A}(A) + \pi \,k\,T. \end{aligned}$$

Since P is also the center of the circumscribed circle to the triangle ABC, which has radius a, then the power of P to this circle is simply $-a^2$, from which the result follows. $\square$