Abstract
In this work, we use the energy and angular momentum integrals as a resource for applying Hill's approach to the general three-body problem. As a result, we obtain theorems on the Lagrange stability and Hill stability in the general three-body problem. Also, specific features of the general and restricted three-body problems are discussed.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Now, in the era of active space exploration, the three-body problem has quite rightly grown from a purely academic problem to an applied one. Computer modeling, analytical methods, and numerical methods (the development of which was largely stimulated by the three-body problem itself) have made it possible to achieve noticeable success in its research (Marchal 1990; Arnold et al. 2002; Celletti 2010; Georgakarakos 2008). Nevertheless, the problem remains unsolved in full to this day, and the qualitative study of the motion in the system is still relevant. Within the framework of this study, it is still important, both from theoretical and practical viewpoints, to find the conditions under which three bodies remain in a bounded region of Euclidean space. Below, based on Hill's approach to the circular restricted three-body problem, we indicate sufficient conditions that ensure the bounded motion in the case of the general three-body problem.
As basic equations, we consider the three-body problem in the form (Sosnitskii 2008):
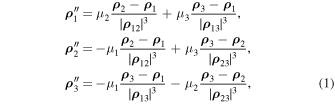
where the prime sign means differentiation with respect to τ (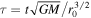 ), μi
= mi
/M, M = m1 + m2 + m3, r0 is a parameter having the dimension of a unit of length. In Equation (1),
ρ
i
=
r
i
/r0 (i = 1, 2, 3), where
r
i
are radius vectors of points in an inertial reference system with the origin at the center of mass for mi
. The parameter r0 with the dimension of a unit length is introduced in order to subsequently work with dimensionless quantities, which is very convenient for our presentation.
), μi
= mi
/M, M = m1 + m2 + m3, r0 is a parameter having the dimension of a unit of length. In Equation (1),
ρ
i
=
r
i
/r0 (i = 1, 2, 3), where
r
i
are radius vectors of points in an inertial reference system with the origin at the center of mass for mi
. The parameter r0 with the dimension of a unit length is introduced in order to subsequently work with dimensionless quantities, which is very convenient for our presentation.
If we set μ3 = 0 in Equations (1), then we arrive at the restricted three-body problem:

where
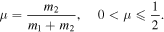
Since
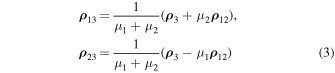
and for the restricted three-body problem,
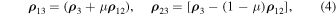
it is also useful to consider the following representations of systems (1) and (2):
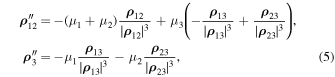
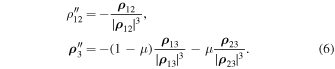
2. On Bounded Motions in the Circular Restricted Three-body Problem
Although it is a rather simplified model of the motion of three bodies (Szebehely 1967; Roy 1978), nevertheless, the circular restricted problem of three bodies (material points) finds many interesting applications even today (Makó & Szenkovits 2008; Szebehely 1967; Lian et al. 2013; Georgakarakos 2008; Qi & Xu 2014; Song et al. 2016; Salazar et al. 2017).
As Jacobi showed, it admits an integral

where ρ13 = ∣
ρ
13∣, ρ23 = ∣
ρ
23∣ and the expression  on the left side of equality (7) is the projection of the angular momentum of the small particle onto the axis O
ζ in an inertial reference frame O
ξ
η
ζ. The O
ζ axis is perpendicular to the O
ξ
η plane in which two massive bodies move. As we see, the Jacobi integral is the sum of the energy of the small particle and the projection of its angular momentum onto the O
ζ axis.
on the left side of equality (7) is the projection of the angular momentum of the small particle onto the axis O
ζ in an inertial reference frame O
ξ
η
ζ. The O
ζ axis is perpendicular to the O
ξ
η plane in which two massive bodies move. As we see, the Jacobi integral is the sum of the energy of the small particle and the projection of its angular momentum onto the O
ζ axis.
The existence of the Jacobi integral in the circular restricted three-body problem allowed Hill (Hill 1878) to prove the existence of bounded motions of the small particle in the case where the level constant h* of the Jacobi integral is negative and ∣h*∣ exceeds some critical value  . In what follows, this condition will be referred to as the Hill condition. If it holds, then the region of possible motions of the infinitesimal particle is the union of the region ωH
of bounded motions in coordinates (Hill region) and the region ωnc
of bounded motions in velocities, i.e., ω = ωH
∪ ωnc
, and ωH
∩ ωnc
= Ø. A distinctive feature of the region ωnc
is that it is free from collisions of bodies (material points). This explains the choice of the nc index to denote this region. Unlike ωH
, the region ωnc
is not bounded, which raises the problem of bounded motion of the small particle in ωnc
. However, relatively recently (Sosnitskii 2018), we managed to prove the boundedness of motions of the small particle belonging to ωnc
.
. In what follows, this condition will be referred to as the Hill condition. If it holds, then the region of possible motions of the infinitesimal particle is the union of the region ωH
of bounded motions in coordinates (Hill region) and the region ωnc
of bounded motions in velocities, i.e., ω = ωH
∪ ωnc
, and ωH
∩ ωnc
= Ø. A distinctive feature of the region ωnc
is that it is free from collisions of bodies (material points). This explains the choice of the nc index to denote this region. Unlike ωH
, the region ωnc
is not bounded, which raises the problem of bounded motion of the small particle in ωnc
. However, relatively recently (Sosnitskii 2018), we managed to prove the boundedness of motions of the small particle belonging to ωnc
.
The structure of the region ω motivates the definitions used below, which relate to both the restricted three-body problem and the general one.
Definition 1. A fixed pair of points  of system (1) is called to be Lagrange stable if the following inequality is satisfied:
of system (1) is called to be Lagrange stable if the following inequality is satisfied:

where  are positive constants.
are positive constants.
Definition 2. A movement  of system (1) is called to be Lagrange stable if the following condition is satisfied:
of system (1) is called to be Lagrange stable if the following condition is satisfied:
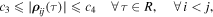
where 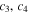 are positive constants.
are positive constants.
Definition 3. We say that the motion 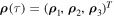 of system (1) is Hill stable if the following condition is satisfied:
of system (1) is Hill stable if the following condition is satisfied:
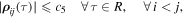
where c5 is positive constant.
Definition 4. We say that the motion  of system (1) is distal if the following inequality is satisfied:
of system (1) is distal if the following inequality is satisfied:
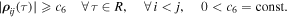
Remark 1. Since the quantities 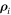 in Equations (1) are relative lengths, without the loss of generality we can further assume in Equation (8) that
in Equations (1) are relative lengths, without the loss of generality we can further assume in Equation (8) that  .
.
In the inertial reference frame O ξ η ζ the Jacobi integral takes the form
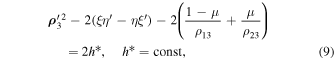
where 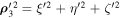 . However, if we use a coordinate system that rotates with unit angular velocity around the O
ζ axis, i.e.,
. However, if we use a coordinate system that rotates with unit angular velocity around the O
ζ axis, i.e.,
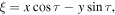
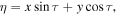
where (x, y, z) are coordinates of the small particle relative to the coordinate system that rotates, the Jacobi integral turns into one of the equalities

or

In this case, the second vector equation of system (6) takes the following form (see Szebehely 1967):
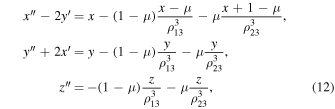
where
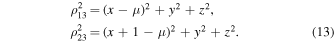
It was the Jacobi integral in the form (11) that Hill used. Within the framework of Hill's approach, for the existence of the regions ωH and ωnc , the determining factor is the inequality
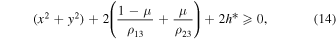
in which the controlled parameter is the level constant h* of the Jacobi integral. As follows from the above definitions, the pair of massive bodies, which is located in the O ξ η plane, is Lagrange stable, and the motions of the small particle belonging to the regions ωH and ωnc are, respectively, Hill stable and Lagrange stable.
As we mentioned above, the Jacobi integral, at least in the inertial coordinate system, is the sum of the energy of the small particle and the projection of its angular momentum onto the O ζ axis. At the same time, it is worth noting that the region ωnc is precisely generated by this projection, which directly follows from Equation (9). If we take into account that the general three-body problem allows both an energy integral and an angular momentum integral, then the question arises whether it is possible to use Hill's approach to obtain conditions for bounded motions in the case of the general three-body problem, at least under additional restrictions. As we will show below, if by analogy with the circular restricted problem we assume the presence of a Lagrange-stable pair in the general three-body problem, then the answer to this question is positive.
3. On Bounded Motions in the General Three-body Problem
In a qualitative study of motion in the case of the three-body problem, the key role is played by the energy integral and the vector integral of the angular momentum, so we are going to use them below. In particular, in accordance with systems (1) and (5), we present the energy integral in the form
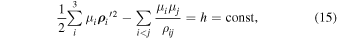
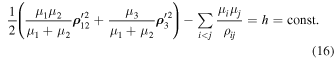
Here ρij = ∣ ρ ij ∣, i, j = 1, 2, 3. Further we restrict ourselves to the case where h < 0.
Along with the usual form of the vector integral of angular momentum
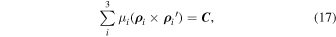
we also present it in the following form (Sosnitskii 2010):
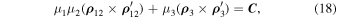
which corresponds to the equations of motion (5). We assume that C ≠ 0.
Further, without loss of generality, we assume that the equality
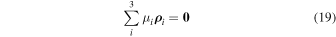
holds, which fixes the origin of the reference system at the center of mass of the material points under consideration.
In our study, we use the above presented forms Equations (16) and (18) of integrals of energy and angular momentum.
Theorem 1. Let a motion 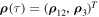 of system (5), which belongs to the set
of system (5), which belongs to the set
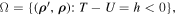
be associated with a Lagrange stable pair 
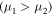 . If, in addition, the motion under consideration corresponds to a sufficiently large constant
. If, in addition, the motion under consideration corresponds to a sufficiently large constant 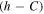 and a sufficiently small mass
and a sufficiently small mass  , then it is either Hill stable or Lagrange stable.
, then it is either Hill stable or Lagrange stable.
Proof. Let us associate the axis 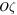 of the inertial reference frame
of the inertial reference frame 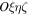 with the direction of the angular momentum
with the direction of the angular momentum 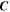 . Then the projection of equality (18) onto the
. Then the projection of equality (18) onto the 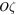 axis takes the form
axis takes the form
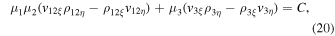
where

Let us rewrite equality (16) as follows:
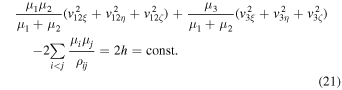
Multiplying it by 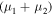 and subtracting from it equality (20) multiplied by two, we arrive at the equality
and subtracting from it equality (20) multiplied by two, we arrive at the equality
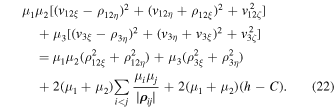
Based on (22), we obtain the inequality
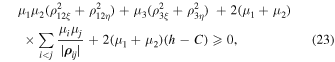
which, for convenience in our further study, can be rewritten in the form
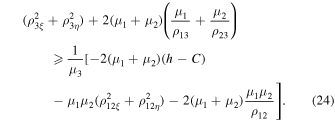
From here, in particular, we conclude that the zero surface corresponding to the transformation of the left-hand side of equality (22) to zero has the form
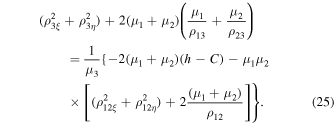
As we see, within the framework of the three-dimensional coordinate space related to 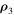 , this surface is pulsating, and the smaller
, this surface is pulsating, and the smaller  , the less this pulsation. To verify this, in contrast to the circular restricted problem, where the zero surface has the form
, the less this pulsation. To verify this, in contrast to the circular restricted problem, where the zero surface has the form
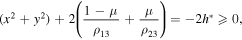
in the present case it is enough to note that the right-hand side of equality (25) contains a variable term ![${\mu }_{1}{\mu }_{2}[...]$](https://content.cld.iop.org/journals/1538-3881/167/5/198/revision3/ajad335dieqn25.gif) in addition to the constant term. This reflects the fact that the distance
in addition to the constant term. This reflects the fact that the distance 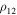 changes over time. Since the first term prevails over the second one according to the conditions of Theorem 1, it is quite natural to say in this case that the zero surface defined by Equation (25) is pulsating. Of course, it is true within the framework of the three-dimensional coordinate space generated by
changes over time. Since the first term prevails over the second one according to the conditions of Theorem 1, it is quite natural to say in this case that the zero surface defined by Equation (25) is pulsating. Of course, it is true within the framework of the three-dimensional coordinate space generated by 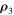 . Let us also recall here that for the original system of equations in the form (5), the dimension of the coordinate space is twice as large.
. Let us also recall here that for the original system of equations in the form (5), the dimension of the coordinate space is twice as large.
Due to the equality
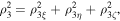
even more so, based on Equation (24), the following inequality is true:
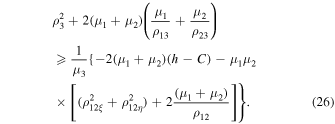
Since
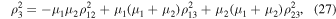
Equation (26) can be represented in the form

Taking into account that  and using Equation (28), we arrive at the inequality
and using Equation (28), we arrive at the inequality
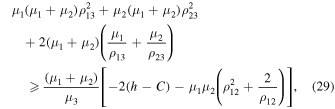
and this implies that
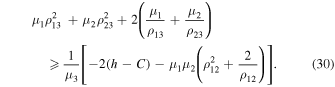
If the conditions of the theorem are met, then according to Equation (30) either both distances  and
and 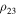 are very large, or one of the distances
are very large, or one of the distances 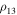 and
and 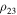 is very small.
is very small.
If 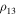 or
or 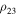 is very small, then due to Equation (30) for the region ω3H
of possible motions, we respectively obtain approximate inequalities
is very small, then due to Equation (30) for the region ω3H
of possible motions, we respectively obtain approximate inequalities
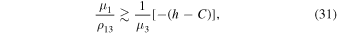
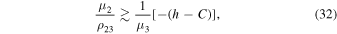
and thus the considered motion of Equation (5) is Hill stable. Here, the notation ω3H
corresponds to the fact that, under the conditions of Theorem 1, the region of possible motions is an analog of the Hill region in the circular restricted problem, and, as in Hill's case, we relate this region to the three-dimensional coordinate space generated by 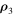 .
.
Now let both distances 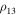 and
and 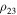 be large. Taking into account (27), we rewrite inequality (30) in the form
be large. Taking into account (27), we rewrite inequality (30) in the form

and, therefore, under the conditions of the theorem, we obtain the approximate inequality
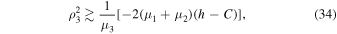
which determines the area of distal movements 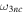 . Again, the notation
. Again, the notation  reflects the fact that the region
reflects the fact that the region 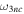 , which we associate with the three-dimensional coordinate space generated by
, which we associate with the three-dimensional coordinate space generated by 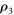 , is free from collisions of bodies (material points) under the conditions of Theorem 1.
, is free from collisions of bodies (material points) under the conditions of Theorem 1.
Due to Theorem 2 from Sosnitskii (2020), the motion under study belonging to 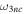 is Lagrange stable. The proof of Theorem 1 is completed.
is Lagrange stable. The proof of Theorem 1 is completed. 
Remark 2. Despite all the similarities between the proposed approach and Hill's approach, there is a fundamental difference between the situations in the circular restricted problem and the general three-body problem. Theorem 1 above deals exclusively with a fixed motion accompanied by a Lagrange-stable pair. Unfortunately, the conditions of the theorem do not exclude the possibility that in the vicinity of this motion there may be both motions for which such a pair exists and motions for which such a pair does not exist. Under the conditions of the circular restricted three-body problem, all motions are always accompanied by the same Lagrange-stable pair, and therefore the regions 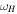 and
and  , in contrast to ω3H
and
, in contrast to ω3H
and 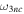 , consist entirely of bounded and distal movements, respectively. In addition, in contrast to the circular restricted three-body problem, an essential requirement in the resulting theorem is smallness of one of the masses in the pair. This is a consequence of the fact that we consider the zero surface in a narrower three-dimensional configuration space compared to the dimension of the original system, which is associated with
, consist entirely of bounded and distal movements, respectively. In addition, in contrast to the circular restricted three-body problem, an essential requirement in the resulting theorem is smallness of one of the masses in the pair. This is a consequence of the fact that we consider the zero surface in a narrower three-dimensional configuration space compared to the dimension of the original system, which is associated with  , making the influence of distances
, making the influence of distances  to estimates in Equations (31), (32), and (34) negligible because of the smallness of
to estimates in Equations (31), (32), and (34) negligible because of the smallness of 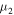 . However, the relationship between the term
. However, the relationship between the term 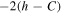 and terms containing the factor
and terms containing the factor 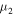 is still more convenient to evaluate if we take into account the inequality in Equation (8). Taking Equation (8) into account, Equation (33) can be represented as
is still more convenient to evaluate if we take into account the inequality in Equation (8). Taking Equation (8) into account, Equation (33) can be represented as
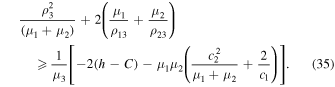
Although we obtain a rougher inequality in this case, however, unlike Equation (33), it contains only constant quantities in its right-hand side.
Remark 3. If we assume that we can measure the mutual distances 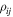 at any time, then, using Equation (30), we can obtain an upper estimate for the constant
at any time, then, using Equation (30), we can obtain an upper estimate for the constant 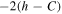 .
.
Considering Equations (30) and (33) as key inequalities in the proof of Theorem 1, it is worth noting that their right-hand sides are divided by μ3. Therefore, if we assume that μ3 is small, then the absolute value of the right-hand sides can be significantly influenced not only by the constant −2(h − C) and the mass μ2, but also by the mass μ3. Thus, due to the smallness of μ3, this makes it possible to weaken the influence of μ2 on the absolute value of the right-hand sides of Equations (30) and (33). This fact is reflected in the following assertion.
Remark 4. Let a motion 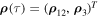 of Equation (5), which belongs to the set
of Equation (5), which belongs to the set
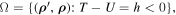
be associated with a Lagrange stable pair 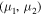
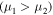 . If, in addition, the motion under consideration corresponds to a sufficiently large constant
. If, in addition, the motion under consideration corresponds to a sufficiently large constant 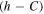 and a sufficiently small mass
and a sufficiently small mass 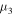 , then it is either Hill stable or Lagrange stable whenever the inequality
, then it is either Hill stable or Lagrange stable whenever the inequality
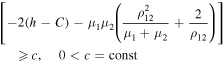
is satisfied.
To prove Theorem 2, we can use the previous scheme, but in this case in accordance with the conditions of the theorem, we have to use inequalities
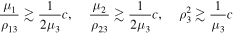
instead of the final inequalities in Equations (31), (32), and (34).
4. Conclusion
Analyzing the structure of the Jacobi integral in the circular restricted three-body problem, we propose an approach based on Hill's idea adapted to the general case of the three-body problem. As a result, we obtain theorems on the Lagrange stability and Hill stability in the general three-body problem. The theorems obtained can serve as additions to Theorem 2 from Sosnitskii (2020).



