Abstract
In this paper, we introduce an \(H({\text {div}})\) finite element method on polygonal and polyhedral meshes for solving the Stokes equations in the primary velocity–pressure formulation. An \(H({\text {div}})\) finite element on polygons or polyhedra is introduced to approximate the velocity so that the method is pressure robust and produces exact divergence free solutions, when the discontinuous \(P_k\) finite element is adopted for the pressure approximation. In addition, this method is stabilizer-free, in handling the \(H^1\) non-conformity. Optimal order error estimates are established for the method. Numerical tests are conducted to confirm the theory.
Similar content being viewed by others
1 Introduction
In this paper, we solve numerically the following Stokes problem: Find unknown velocity \(\textbf{u}\) and pressure p such that
where \(\mu \) denotes the fluid viscosity and \(\Omega \) is a 2D polygonal domain, or a 3D polyhedral domain.
The Stokes equations have many applications in fluid dynamics, especially for linearizing the famous Navier-Stokes equations. Finite element methods for the Stokes equations have been studied extensively. Finite element methods in the velocity–pressure formulation have been studied in Crouzeix and Raviart (1973); Girault and Raviart (1986) by \(H^1\) conforming and nonconforming finite element methods, in Schotzau et al. (2003) by discontinuous Galerkin finite element methods, and in Chen et al. (2016); Liu et al. (2020); Mu (2020); Wang et al. (2016) by weak Galerkin finite element methods. In particular, \(H^1\) divergence-free finite element methods are pressure-robust and produce exactly divergence free solutions, cf. (Arnold and Qin 1992; Fabien et al. 2022; Falk and Neilan 2013; Guzman and Neilan 2014a, b, 2018; Huang and Zhang 2012, 2011, 2013; Kean et al. 2022; Neilan 2015; Neilan and Otus 2021; Neilan and Sap 2016; Qin and Zhang 2007; Scott and Vogelius 1985; Xu and Zhang 2010; Zhang 2005, 2008, 2009, 2011a, b, 2017, 2024). In Wang et al. (2009); Wang and Ye (2007), an \(H({\text {div}})\) finite element method on triangular meshes is proposed for the Stokes equations, i.e. the velocity is approximated by \(H({\text {div}})\) finite elements. Therefore the resulting solutions are also exactly divergence free, and consequently the method is pressure robust (John et al. 2017).
Since the finite element solutions in \(H({\text {div}})\) space are discontinuous in tangential directions, a stabilizer is introduced in Wang et al. (2009); Wang and Ye (2007), enforcing some weak continuity of velocity approximation in tangential directions. One would remove such stabilizers in discontinuous finite element methods if possible, for simplifying the methods and reducing the computational cost. The stabilizer-free weak Galerkin and the stabilizer-free discontinuous Galerkin methods on polytopal meshes were first introduced in Ye and Zhang (2020a, 2020c) respectively, for second order elliptic problems. The method has been improved in Al-Taweel and Wang (2020) and applied to the Stokes equations (Feng et al. 2022; Mu et al. 2021; Peng et al. 2021; Ye and Zhang 2021a) and the biharmonic equation (Ye and Zhang 2020e, 2023). Recently, we developed a stabilizer free \(H({\text {div}})\) finite element method in Ye and Zhang (2021b) for the Stokes problem on triangular and tetrahedral meshes. The method is extended to tensor-product meshes in Mu et al. (2023). The method is improved in 2D by finding the divergence-free subspace of \(H({\text {div}})\) finite element space on triangular meshes (Ye and Zhang 2021c). To obtain a stabilizer-free \(H({\text {div}})\) finite element method in Ye and Zhang (2021b), a technique is adopted from the conforming discontinuous Galerkin method (Ye and Zhang 2020b, c, d, 2022a, b). This work is to extend the stabilizer-free \(H({\text {div}})\) finite element method (Ye and Zhang 2021b) on triangular/tetrahedral meshes to polytopal meshes.
So far most existing \(H({\text {div}})\) finite elements (Brezzi and Fortin 1991) are defined on triangles or rectangles in 2D and tetrahedra or cuboids in 3D, respectively. It is far from trivial to construct \(H({\text {div}})\) finite elements on polygons/polyhedra, for the required normal-continuity on too many edges/face-polygons. Wachspress coordinates are used in Chen and Wang (2017) to construct a lowest order \(H({\text {div}})\) element on convex polygons and polyhedra, which are not polynomials, but rational functions. RT-type \(H({\text {div}})\) finite elements on polytopal meshes are constructed in Lin et al. (2022), and are applied to a one-order superconvergent discontinuous Galerkin finite element method (Ye and Zhang 2020c). But for the Stokes equations, we need BDM-type \(H({\text {div}})\) finite elements on polytopal meshes in order to have an optimal-order discretization. BDM-type \(H({\text {div}})\) finite elements on polytopal meshes are constructed and applied to a two-order superconvergent discontinuous Galerkin finite element method in Ye and Zhang (2020d). More BDM-type \(H({\text {div}})\) finite elements on polytopal meshes are constructed in Xu et al. (2024), covering more polyhedra in 3D.
In this work, we adopt the BDM-type \(H({\text {div}})\) finite elements on polytopal meshes (Ye and Zhang 2020d; Xu et al. 2024) to approximate the velocity and the discontinuous \(P_k\) polynomials to approximate the pressure, in solving the Stokes equations. Again, this method is stabilizer free and pressure robust. In addition, the \(H({\text {div}})\) velocity solution is divergence free. The optimal order error estimates are established for both velocity and pressure finite element approximations. The pressure-robustness of the method is proved in the theory, and confirmed in numerical tests.
2 Polytopal BDM-type H-div finite elements
2.1 2D polygons
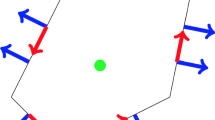
Let \(T\in \mathcal {T}_h\) be a n-polygon, cf. Fig. 1. We assume T can be subdivided into \(n-2\) shape regular triangles by connecting one vertex \(\textbf{x}_1\) with vertices \(\textbf{x}_3\), ..., \(\textbf{x}_{n-1}\). We define \(\textbf{H}_k(T)\) for the BDM \(H({\text {div}})\) finite element space on T as
We construct here a subspace of \(H({\text {div}}; T)\) which has a one piece divergence,
We specify the degrees of freedom, i.e., a basis \(\{F_i\}\) for the linear functional space on \(\textbf{H}_k(T)\), as follows.
where edge \(e_{j,j+1}=\textbf{x}_j\textbf{x}_{j+1}\), \(\textbf{x}_{n+1}=\textbf{x}_1\), \(\textbf{n}\) is a fixed unit normal vector on the edge, \(T_j=\textbf{x}_1\textbf{x}_{j+1}\textbf{x}_{j+2}\), \(\nabla ^\perp f = \langle -\partial _y f, \partial _x f\rangle \), and \(B=\lambda _1\lambda _2\lambda _3\) with the barycentric coordinates (i.e., the linear function \(\lambda _i=0\) on one edge of the triangle \(T_j\) and \(\lambda _i=1\) at the opposite vertex.)
We specify next the continuity constraints on the functions of \(\textbf{H}_{k}(T)\) to eliminate the extra degrees of freedom,
where \([\cdot ]\) denotes the jump on the edge, and \(\textbf{u}|_{T_j}\in {[}P_k(T_j)]^3\) is viewed as \(\textbf{u}|_{T_j}\in [P_k(T_1\cup T_j)]^3\). We note that the number of constraints plus the number of degrees of freedom is exactly equal to \(2 n \dim P_k\).
2.2 Type-one polyhedra
We consider one type of polyhedron which can be subdivided in to tetrahedra without introducing any internal edge.
Let \(T\in \mathcal {T}_h\) be an m-polygon-face polyhedron, cf. Fig. 2. Let \(F_i\) be a face polygon of T. We subdivide it into \(f_i\) (may have \(f_i=1\) triangles \(\{ e_{i,1},\dots ,e_{i,f_i}\}\). Together we get \(M=4n-2(n-1)\) face-triangles, where n is the number of tetrahedra after the subdivision. With these M triangles and no internal edge introduced, we assume T is subdivided into n shape regular tetrahedra, \(\{T_1,\dots ,T_n\}\). Between \(T_i\) and \(T_{i+1}\), we have one internal triangle \(t_i\). There are \((n-1)\) internal triangles \(t_i\) separating the n tetrahedra.
An m-face (\(m=5\) in the figure) polyhedron is subdivided in to n (\(n=3\)) tetrahedra, where there is no internal edge, there are exactly \((n-1)\) internal triangles, a face polygon \(F_i\) is subdivided into \(f_i\) (\(f_i=1\) or 2 in the figure) triangles \(\{e_{i1},\dots ,e_{i,f_i}\}\), and there are M outside face triangles
We define the 3D BDM \(H({\text {div}})\) macro-element space on T as
We specify the degrees of freedom, the set \(\{F_l(\textbf{u}) \}\) of the linear functionals, as follows.
where the curl space
We specify the constraints on the base polynomial space \(\prod _{i=1}^n P_k(T_i)^3\) as follows.
where \(\textbf{u}|_{e_{ij}}\in [P_k(e_{ij})]^3\) is viewed as \(\textbf{u}|_{e_{ij}}\in [P_k(e_{i1}\cup e_{ij})]^3\), \([\textbf{u}]\) is the jump of \(\textbf{u}\) at triangle \(t_i\), and \(\textbf{u}|_{T_i}\in [P_k(T_i)]^3\) is viewed as \(\textbf{u}|_{T_i}\in [P_k(T_1\cup T_i)]^3\).
2.3 Type-two polyhedra
Let \(T\in \mathcal {T}_h\) be an m-polygon-face polyhedron, cf. Fig. 3. Let \(F_i\) be a face polygon of T. We subdivide it into \(f_i\) triangles \(\{ e_{i,1},\dots ,e_{i,f_i}\}\). Together we get \(M=2n\) face-triangles. With these M triangles and exactly one internal edge (connecting two vertices), we assume T is subdivided into n shape regular tetrahedra, \(\{T_1,\dots ,T_n\}\). Between \(T_i\) and \(T_{i+1}\), we have one internal triangle \(t_i\). \(t_n\) is the triangle between \(T_n\) and \(T_1\).
An m-face (\(m=6\) in the figure) polyhedron is subdivided in to n (\(n=6\)) tetrahedra, where there is exactly one internal edge, there are exactly n internal triangles, a face polygon \(F_i\) is subdivided into \(f_i\) (\(f_i=2\)) triangles \(\{e_{i1},\dots ,e_{i,f_i}\}\), and there are M face triangles
We define the 3D BDM \(H({\text {div}})\) macro-element space on T as
We specify the degrees of freedom, the set \(\{F_l(\textbf{u}) \}\) of the linear functionals, as follows.
where the curl space \(\textbf{CP}_k(T_j)\) is defined in (2.6), and \(t_1\) is an internal triangle which is on a tetrahedron having two other face-triangles on \(\partial T\).
We specify the constraints on the base polynomial space \(\prod _{i=1}^n P_k(T_i)^3\) as follows.
where \(\textbf{u}|_{e_{ij}}\in [P_k(e_{ij})]^3\) is viewed as \(\textbf{u}|_{e_{ij}}\in [P_k(e_{i1}\cup e_{ij})]^3\), \([\textbf{u}]\) is the jump of \(\textbf{u}\) at triangle \(t_i\), and \(\textbf{u}|_{T_i}\in [P_k(T_i)]^3\) is viewed as \(\textbf{u}|_{T_i}\in [P_k(T_1\cup T_i)]^3\).
3 The finite element
Let \(\mathcal {T}_h\) be a partition of the domain \(\Omega \) consisting of polygons in two dimensions or polyhedra in three dimensions satisfying subdivision conditions specified in last section. For every element \(T\in \mathcal {T}_h\), we denote by \(h_T\) its diameter. We let mesh size \(h=\max _{T\in \mathcal {T}_h} h_T\) for \({\mathcal T}_h\).
The space \(H({\text {div}};\Omega )\) is defined as the set of vector-valued functions on \(\Omega \) which, together with their divergence, are square integrable; i.e.,
For any \(T\in \mathcal {T}_h\), it can be divided in to a set of disjoint triangles/tetrahedrons \(T_i\) with \(T=\cup T_i\), specified in the last section. We define the \(H({\text {div}})\) finite element space \(V_h\) for velocity approximation as, for \(k\ge 1\),
where \(\textbf{H}_k(T)\) is defined in (2.1), or (2.4), or (2.8). As we define the degrees of freedom locally, not on a reference element, the dual (i.e., computational) basis functions in (3.1) are local too, not mapped from a set of reference functions.
The following lemma is proved in Ye and Zhang (2021a).
Lemma 3.1
The interpolation operator \(\Pi _h: [H^1_0(\Omega )]^d \rightarrow V_h\), defined by the degrees of freedom (2.2), (2.5) or (2.9), satisfies
Let \(T_1\) and \(T_2\) be two triangles/tetrahedrons in \(T\in \mathcal {T}_h\) sharing e. For \(\textbf{v}\in V_h+[H_0^1(\Omega )]^d \), we define jump \([\textbf{v}]\) as
and the average \(\{v\}\) as
The order of \(T_1\) and \(T_2\) is not essential.
For a function \(\textbf{v}\in V_h+[H_0^1(\Omega )]^d\), its weak gradient is a piecewise polynomial satisfying \(\nabla _w\textbf{v}|_{T_i} \in [P_{k+1}(T_i)]^{d\times d}\) and
Let \(\mathbb {Q}_h\) be the element-wise defined \(L^2\) projection onto the space \([P_{k+1}(T_i)]^{d\times d}\) on \(T_i\).
Lemma 3.2
Let \(\varvec{\phi }\in [H_0^1(\Omega )]^d\), then on \(T_i\subset T\in \mathcal {T}_h\)
Proof
Using (3.4) and integration by parts, we have that for any \(\tau \in [P_{k+1}(T_i)]^{d\times d}\)
which implies the identity (3.5). \(\square \)
For \(k\ge 1\) and given \(\mathcal {T}_h\), we define the finite element space for the pressure approximation,
We introduce the following finite element scheme without stabilizers.
Algorithm 1
A numerical approximation for (1.1)–(1.3) can be obtained by seeking \(\textbf{u}_h\in V_h\) and \(p_h\in W_h\) such that for all \(\textbf{v}\in V_h\) and \(q\in W_h\),
where \(V_h\) and \(W_h\) are defined in (3.1) and (3.6), respectively.
For any function \(\varphi \in H^1(T)\), the following trace inequality holds true (see Wang and Ye 2014 for details):
We introduce two semi-norms \({|\hspace{-.02in}|\hspace{-.02in}|} \textbf{v}{|\hspace{-.02in}|\hspace{-.02in}|}\) and \(\Vert \textbf{v}\Vert _{1,h}\) for any \(\textbf{v}\in V_h \cup [H^1(\Omega )]^d\) as follows:
where \(T=\cup _iT_i\). It is easy to see that \(\Vert \textbf{v}\Vert _{1,h}\) defines a norm in \(V_h\).
Lemma 3.3
There exist two positive constants \(C_1\) and \(C_2\) such that for any \(\textbf{v}\in V_h\), we have
where the semi-norms are defined in (3.10)–(3.11).
Lemma 3.3 has been proved in Ye and Zhang (2020c); Al-Taweel and Wang (2020).
Lemma 3.4
There exists a positive constant \(\beta \) independent of h such that for all \(\rho \in W_h\),
Proof
We note that the interpolation operator \(\Pi _h\) introduced in (3.2) and (3.3) is defined locally, not on a reference macro-element. For any given \(\rho \in W_h\subset L_0^2(\Omega )\), it is known (Girault and Raviart 1986) that there exists a function \({\tilde{\textbf{v}}}\in [H_0^1(\Omega )]^d\) such that
where \(C>0\) is a constant independent of h. Let \(\textbf{v}=\Pi _h\tilde{\textbf{v}}\in V_h\). It follows from (3.12), (3.9), (3.3) and \(\tilde{\textbf{v}}\in [H_0^1(\Omega )]^d\),
which implies
It follows from (3.2) that
Using the above Eqs. (3.14) and (3.15), we have
for a positive constant \(\beta \). This completes the proof of the lemma. \(\square \)
Lemma 3.5
The weak Galerkin method (3.7)–(3.8) has a unique solution.
Proof
It suffices to show that zero is the only solution of (3.7)–(3.8) if \(\textbf{f}=\textbf{0}\). To this end, let \(\textbf{f}=\textbf{0}\) and take \(\textbf{v}=\textbf{u}_h\) in (3.7) and \(q=p_h\) in (3.8). By adding the two resulting equations, we obtain
which implies that \(\nabla _w \textbf{u}_h=0\) on each element T. By (3.12), we have \(\Vert \textbf{u}_h\Vert _{1,h}=0\) which implies that \(\textbf{u}_h=0\).
Since \(\textbf{u}_h=\textbf{0}\) and \(\textbf{f}=\textbf{0}\), the Eq. (3.7) becomes \((\nabla \cdot \textbf{v},\ p_h)=0\) for any \(\textbf{v}\in V_h\). Then the inf-sup condition (3.13) implies \(p_h=0\). We have proved the lemma. \(\square \)
4 Error equations
In this section, we will derive the equations that the errors satisfy. First we define an element-wise \(L^2\) projection \(Q_h\) onto the local space \(P_{k-1}(T)\) for \(T\in \mathcal {T}_h\). Let \(\textbf{e}_h=\Pi _h\textbf{u}-\textbf{u}_h\), \(\textbf{E}_h=\textbf{u}-\textbf{u}_h\) and \(\varepsilon _h=Q_hp-p_h\).
Lemma 4.1
The following error equations hold true for any \(\textbf{v}\in V_h\) and \(q\in W_h\),
where
Proof
First, we test (1.1) by \(\textbf{v}\in V_h\) to obtain
Integration by parts gives
where we use the fact \(\sum _{T\in \mathcal {T}_h}\sum _i\langle \nabla \textbf{u}\cdot \textbf{n},\{\textbf{v}\}\rangle _{{\partial T}_i}=0\). It follows from integration by parts, (3.4) and (3.5),
Combining (4.6) and (4.7) gives
Using integration by parts and \(\textbf{v}\in V_h\), we have
Substituting (4.8) and (4.9) into (4.5) gives
The difference of (4.10) and (3.7) implies
Adding and subtracting \(( \mu \nabla _w\Pi _h\textbf{u},\nabla _w\textbf{v})\) in (4.11), we have
which implies (4.1).
Testing Eq. (1.2) by \(q\in W_h\) and using (3.2) give
The difference of (4.12) and (3.8) implies (4.2). We have proved the lemma. \(\square \)
5 Error estimates in energy norm
In this section, we shall establish optimal order error estimates for the velocity approximation \(\textbf{u}_h\) in \({|\hspace{-.02in}|\hspace{-.02in}|}\cdot {|\hspace{-.02in}|\hspace{-.02in}|}\) norm and for the pressure approximation \(p_h\) in the standard \(L^2\) norm.
Lemma 5.1
Let \(\textbf{w}\in [H^{k+1}(\Omega )]^d\) and \(\textbf{v}\in V_h\). Then, the following estimates hold true
where \(\ell _1\) and \(\ell _2\) are defined in (4.3) and (4.4), respectively.
Proof
Using the Cauchy–Schwarz inequality, the trace inequality (3.9), and (3.12), we have
Next we estimate \(|\ell _2(\textbf{w}, \textbf{v})|=|( \mu \nabla _w (\textbf{w}-\Pi _h\textbf{w}),\nabla _w\textbf{v})|\). It follows from (3.4), integration by parts, (3.9) and (3.3) that for any \(\textbf{q}\in [P_{k+1}(T_i)]^{d\times d}\),
Letting \(\textbf{q}=\nabla _w\textbf{v}\) in the above equation and taking summation over \(T_i\), we have
Letting \(\textbf{q}=\nabla _w(\textbf{w}-\Pi _h\textbf{w})\) in (5.4) implies (5.3). We have proved the lemma. \(\square \)
Theorem 5.1
Let \((\textbf{u}_h,p_h)\in V_h^0\times W_h\) be the solution of (3.7)–(3.8). Then, the following error estimates hold true
Proof
By letting \(\textbf{v}=\textbf{e}_h\) in (4.1) and \(q=\varepsilon _h\) in (4.2) and using (4.2), we have
By (5.7), it then follows from (5.1) and (5.2) that
By the triangle inequality, (5.3) and (5.8), (5.5) holds. To estimate \(\Vert \varepsilon _h\Vert \), we have from (4.1) that
Using the equation above, (5.8), (5.1) and (5.2), we arrive at
Combining the above estimate with the inf-sup condition (3.13) gives
which yields the estimate (5.6) and completes the proof of the theorem. \(\square \)
6 Error estimates in \(L^2\) norm
In this section, we shall derive an \(L^2\)-error estimate for the velocity approximation through a duality argument. Recall that \(\textbf{e}_h=\Pi _h\textbf{u}-\textbf{u}_h\) and \(\textbf{E}_h=\textbf{u}-\textbf{u}_h\). To this end, consider the problem of seeking \((\textbf{U},\xi )\) such that
Assume that the dual problem has the \([H^{2}(\Omega )]^d\times H^1(\Omega )\)-regularity property in the sense that the solution \((\textbf{U},\xi )\in [H^{2}(\Omega )]^d\times H^1(\Omega )\) and the following a priori estimate holds true:
Lemma 6.1
For \(\textbf{E}_h=\textbf{u}-\textbf{u}_h\) and \(\ell _1(\cdot ,\cdot )\) defined in (4.3), the following equation holds true,
where
Proof
Testing (6.1) by \(\textbf{E}_h\) gives
Using integration by parts, (3.4) and the fact \(\sum _{T\in \mathcal {T}_h}\sum _i{\langle }\nabla \textbf{U}\cdot \textbf{n},\{\textbf{E}_h\}{\rangle }_{{\partial T}_i}=0\), then
It follows from (3.5) that
The two equations above imply that
Letting \(\textbf{v}=\Pi _h\textbf{U}\) in (4.11) gives
It follows from (3.2) and (6.2)
Using(6.9), the Eq. (6.6) becomes
It follows from integration by parts and (1.2) and (3.8)
Combining (6.10)–(6.11) with (6.5), we have obtained (6.4). \(\square \)
Theorem 6.1
Let \((\textbf{u}_h,p_h)\in V_h\times W_h\) be the solution of (3.7)–(3.8). Assume that (6.3) holds true. Then, we have
Proof
By Lemma 6.1, we have
Next we will estimate all the terms on the right hand side of (6.13). Using the Cauchy–Schwarz inequality, the trace inequality (3.9) and the definitions of \(\Pi _h\) and \(\mathbb {Q}_h\) we obtain
It follows from (5.3) and (5.5) that
The norm equivalence (3.12) and (5.8) imply
Using (3.12) and (5.8), we obtain
Combining all the estimates above with (6.4) yields
The estimate (6.12) follows from the above inequality and the regularity assumption (6.3). We have completed the proof. \(\square \)
7 Numerical experiments
In the 2D numerical test, we solve the Stokes equations (1.1)–(1.3) on the domain of unit square \(\Omega =(0,1)^2\). We choose an exact solution
where \(g(x,y)=2^6 x^2(1-x)^2 y^2 (1-y^2)\). We compute this problem on the uniform rectangular meshes shown in Fig. 4. Though we have rectangular meshes, we do not use the rectangular BDFM \(H({\text {div}})\) finite element, but the new macro-triangular \(H({\text {div}})\) finite element, \(V_h\) defined in (3.1). We list the numerical results in Tables 1, 2, 3 and 4. Optimal orders of convergence are achieved in all cases, for all variables, all degree elements, and in all norms. We can see the method is pressure robust, as the error of \(\textbf{u}_h\) is independent of the viscosity \(\mu \). When computing \(P_4\) elements in Table 4, the round-off error is too large that the error of \(\textbf{u}_h\) is affected slightly. As proved in the theory, the pressure error is of order \(O(\mu h^k)\) shown in the tables. Again, when \(\mu =10^{-8}\), the error of \(p_h\) is too small that the round-off error alters the order of convergence.
In the 3D numerical test, we solve the Stokes equations (1.1)–(1.3) on the domain of unit cube \(\Omega =(0,1)^3\), with a non-homogeneous boundary condition, and an exact solution
We compute the problem on the uniform cubic meshes shown in Fig. 5. Again, we do not use the cubic BDFM \(H({\text {div}})\) finite element, but the new macro-tetrahedral \(H({\text {div}})\) finite element, \(V_h\) defined in (3.1). We list the numerical results in Tables 5 and 6. Optimal orders of convergence are achieved in all cases, for all variables, all degree elements, and in all norms. The method is pressure robust, which implies the error of velocity \(\textbf{u}_h\) remains same as \(\mu \rightarrow 0\). The error of pressure \(p_h\) at \(\mu =10^{-8}\) is precisely \(10^{-8}\) of that at \(\mu =1\).
Data availability
This research does not use any external or author-collected data.
References
Al-Taweel A, Wang X (2020) A note on the optimal degree of the weak gradient of the stabilizer free weak Galerkin finite element method. Appl Numer Math 150:444–451
Arnold DN, Qin J (1992) Quadratic velocity/linear pressure Stokes elements. In: Vichnevetsky R, Steplemen RS (eds) advances in computer methods for partial differential equations VII
Brezzi F, Fortin M (1991) Mixed and hybrid finite elements. Springer-Verlag, New York
Chen G, Feng M, Xie X (2016) Robust globally divergence-free weak Galerkin methods for Stokes equations. J Comput Math 34:549–572
Chen W, Wang Y (2017) Minimal Degree \(H(curl)\) and \(H(\text{ div})\) conforming finite elements on polytopal meshes. Math Comp 86:2053–2087
Crouzeix M, Raviart P (1973) Conforming and nonconforming finite element methods for solving the stationary Stokes equations. RAIRO Anal Numer 7:33–76
Fabien M, Guzman J, Neilan M, Zytoon A (2022) Low-order divergence-free approximations for the Stokes problem on Worsey-Farin and Powell-Sabin splits. Comput Methods Appl Mech Eng 390:114444
Falk R, Neilan M (2013) Stokes complexes and the construction of stable finite elements with pointwise mass conservation. SIAM J Numer Anal 51(2):1308–1326
Feng Y, Liu Y, Wang R, Zhang S (2022) A stabilizer-free weak Galerkin finite element method for the stokes equations. Adv Appl Math Mech 14(1):181–201
Girault V, Raviart P (1986) Finite element methods for the Navier–Stokes equations: theory and algorithms. Springer-Verlag, Berlin
Guzman J, Neilan M (2014) Conforming and divergence-free Stokes elements on general triangular meshes. Math Comp 83(285):15–36
Guzman J, Neilan M (2014) Conforming and divergence-free Stokes elements in three dimensions. IMA J Numer Anal 34(4):1489–1508
Guzman J, Neilan M (2018) inf-sup stable finite elements on barycentric refinements producing divergence-free approximations in arbitrary dimensions. SIAM J Numer Anal 56(5):2826–2844
Huang J, Zhang S (2012) A divergence-free finite element method for a type of 3D Maxwell equations. Appl Numer Math 62(6):802–813
Huang Y, Zhang S (2011) A lowest order divergence-free finite element on rectangular grids. Front Math China 6(2):253–270
Huang Y, Zhang S (2013) Supercloseness of the divergence-free finite element solutions on rectangular grids. Commun Math Stat 1(2):143–162
John V, Linke A, Merdon C, Neilan M, Rebholz L (2017) On the divergence constraint in mixed finite element methods for incompressible flows. SIAM Rev 59:492–544
Kean K, Neilan M, Schneier M (2022) The Scott-Vogelius method for the Stokes problem on anisotropic meshes. Int J Numer Anal Model 19(2–3):157–174
Lin Y, Ye X, Zhang S (2022) A mixed finite-element method on polytopal mesh. Commun Appl Math Comput 4(4):1374–1385
Liu J, Harper G, Malluwawadu N, Tavener S (2020) A lowest-order weak Galerkin finite element method for Stokes flow on polygonal meshes. J Comput Appl Math 368:112479
Mu L (2020) Pressure robust weak Galerkin finite element methods for Stokes problems. SIAM J Sci Comput 42:B608–B629
Mu L, Ye X, Zhang S (2021) A stabilizer free, pressure robust, and superconvergence weak Galerkin finite element method for the Stokes Equations on polytopal mesh. SIAM J Sci Comput 43(4):A2614–A2637
Mu L, Ye X, Zhang S, Zhu P (2023), A DG method for the Stokes equations on tensor product meshes with \([P_k]^d-P_{k-1}\) element. Commun Appl Math Comput
Neilan M (2015) Discrete and conforming smooth de Rham complexes in three dimensions. Math Comp 84(295):2059–2081
Neilan M, Otus B (2021) Divergence-free Scott-Vogelius elements on curved domains. SIAM J Numer Anal 59(2):1090–1116
Neilan M, Sap D (2016) Stokes elements on cubic meshes yielding divergence-free approximations. Calcolo 53(3):263–283
Peng H, Zhai Q, Zhang R, Zhang S (2021) A weak Galerkin-mixed finite element method for the Stokes–Darcy problem. Sci China Math 64(10):2357–2380
Qin J, Zhang S (2007) Stability and approximability of the P1–P0 element for Stokes equations. Int J Numer Methods Fluids 54:497–515
Schotzau D, Schwab C, Toselli A (2003) Mixed \(hp\)-DGFEM for incompressible flows. SIAM J Numer Anal 40:2171–2194
Scott LR, Vogelius M (1985) Norm estimates for a maximal right inverse of the divergence operator in spaces of piecewise polynomials, RAIRO. Model Math Anal Numer 19:111–143
Wang J, Wang Y, Ye X (2009) A robust numerical method for Stokes equations based on divergence-free \(H(\text{ div})\) finite element methods. SIAM J Sci Comput 31:2784–2802
Wang J, Ye X (2007) New finite element methods in computational fluid dynamics by \(H(\text{ div})\) elements. SIAM Numer Anal 45:1269–1286
Wang J, Ye X (2014) A Weak Galerkin mixed finite element method for second-order elliptic problems. Math Comp 83:2101–2126
Wang R, Wang X, Zhai Q, Zhang R (2016) A weak Galerkin finite element scheme for solving the stationary Stokes equations. J Comput Appl Math 302:171–185
Xu X, Zhang S (2010) A new divergence-free interpolation operator with applications to the Darcy-Stokes-Brinkman equations. SIAM J Sci Comput 32(2):855–874
Ye X, Zhang S (2020) A stabilizer-free weak Galerkin finite element method on polytopal meshes. J Comput Appl Math 371:112699
Ye X, Zhang S (2020) A conforming discontinuous Galerkin finite element method. Int J Numer Anal Model 17(1):110–117
Ye X, Zhang S (2020) A conforming discontinuous Galerkin finite element method: Part II. Int J Numer Anal Model 17(2):281–296
Ye X, Zhang S (2020) A conforming discontinuous Galerkin finite element method: Part III. Int J Numer Anal Model 17(6):794–805
Ye X, Zhang S (2020) A stabilizer free weak Galerkin method for the biharmonic equation on polytopal meshes. SIAM J Numer Anal 58(5):2572–2588
Ye X, Zhang S (2021) A stabilizer free WG finite element method on polytopal mesh: Part III. J Comput Appl Math 394:113538
Ye X, Zhang S (2021) A stabilizer-free pressure-robust finite element method for the Stokes equations. Adv Comput Math 47(2):28
Ye X, Zhang S (2021) A stabilizer free WG Method for the Stokes Equations with order two superconvergence on polytopal mesh. Electron Res Arch 29(6):3609–3627
Ye X, Zhang S (2021) A numerical scheme with divergence free H-div triangular finite element for the Stokes equations. Appl Numer Math 167:211–217
Ye X, Zhang S (2022) A \(C^0\)-conforming DG finite element method for biharmonic equations on triangle/tetrahedron. J Numer Math 30(3):163–172
Ye X, Zhang S (2022) A weak divergence CDG method for the biharmonic equation on triangular and tetrahedral meshes. Appl Numer Math 178:155–165
Ye X, Zhang S (2023) Four-order superconvergent weak Galerkin methods for the biharmonic equation on triangular meshes. Commun Appl Math Comput 5:1323
Xu X, Ye X, Zhang S (2024) A macro BDM H-div mixed finite element on polygonal and polyhedral meshes. preprint
Zhang S (2005) A new family of stable mixed finite elements for 3D Stokes equations. Math Comp 74(250):543–554
Zhang S (2008) On the P1 Powell-Sabin divergence-free finite element for the Stokes equations. J Comp Math 26:456–470
Zhang S (2009) A family of \(Q_ k+1, k \times Q_ k, k+1 \) divergence-free finite elements on rectangular grids. SIAM J Numer Anal 47:2090–2107
Zhang S (2011) Quadratic divergence-free finite elements on Powell-Sabin tetrahedral grids. Calcolo 48(3):211–244
Zhang S (2011) Divergence-free finite elements on tetrahedral grids for \(k\ge 6\). Math Comp 80:669–695
Zhang S (2017) A P4 bubble enriched P3 divergence-free finite element on triangular grids. Comput Math Appl 74(11):2710–2722
Zhang S (2024) Neilan’s divergence-free finite elements for Stokes equations on tetrahedral grids. Numer Methods Partial Differ Equ 40:e23055
Acknowledgements
None.
Funding
None
Author information
Authors and Affiliations
Contributions
All authors made equal contribution.
Corresponding author
Ethics declarations
Conflict of Interest
There is no potential conflict of interest .
Consent for publication
The submitted work is original and is not published elsewhere in any form or language.
Ethical approval
This article does not contain any studies involving animals. This article does not contain any studies involving human participants.
Informed consent
This research does not have any human participant.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ye, X., Zhang, S. An H-div finite element method for the Stokes equations on polytopal meshes. Comp. Appl. Math. 43, 184 (2024). https://doi.org/10.1007/s40314-024-02695-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40314-024-02695-6