1 Introduction

The purpose of this paper is to briefly review the matching conditions in perturbation theory to first order involved in the even-parity tidal problem, and present them in a way that are readily applicable to generalizations other than in the known perfect fluid [1,2,3] or two-fluid (to model superfluid) stars [4] contexts.

The aim of studying the tidal problem is to obtain the Love number, or, equivalently, the tidal deformability, of stars. The global problem consists of a region to model the stellar interior which is matched to an exterior vacuum region that models a tidal field, produced e.g. by a companion star. Using perturbation theory the model is built as a first order perturbation on top of a static and spherically symmetric background configuration consisting of an interior region ball of radius \(R_*\) with a Schwarzschild exterior. The Love number is then determined from the value that certain function of the first order metric perturbation, that depends only on the radial coordinate, \(y^-(r)\), takes at the outer surface (the surface as seen from the exterior) of the star, specifically \(y^-(R_*)\). That value is found by integrating an analogous function \(y^+(r)\) in the interior region from the origin outwards to obtain \(y^+(R_*)\), and then use whatever information we have on the jump \([y]:=y^+(R_*)-y^-(R_*)\) to determine \(y^-(R_*)\) (see [5]).

In the context of perfect fluid models, it was argued in [1, 2] that the jump is given by (see Eq. (15) in [2])

$$\begin{aligned}{}[y]=\varkappa \frac{R_*^3}{2M} E(R_*), \end{aligned}$$
(1)

where E is the energy density (of the background configuration), M is the mass of the star, and we use \(\varkappa \) for the gravitational coupling constant (\(\varkappa =8\pi \) in natural units \(G=c=1\)). The argument uses the fact that the function y(r) is defined as the quotient \(r H'(r)/H(r)\), where H is a function that describes part of the first order perturbation (that is the harmonic \(\ell =2\) part of the \(H_0\) function of the Regge–Wheeler decomposition [6]). The problem is set on the whole domain \(r\in (0,\infty )\), and H is implicitly assumed to be continuous at \(r=R_*\), just as well as the rest of the perturbation metric functions. The key idea is that the Einstein field equations (EFE) at first order can be defined (in strict terms at least in a distributional sense), and H(r) thus satisfies a second order ODE that contains a term with dE/dP, where P is the pressure of the background configuration. Therefore, since P(r) must be continuous at the surface, if E(r) has a jump at \(r=R_*\), then dE/dP presents a Dirac delta term there proportional to \(E(R_*)\). As a result, the solution of H(r) yields a continuous function but discontinuous \(H'(r)\) at \(r=R_*\), with a jump \([H']\) proportional to \(E(R_*)\). Completing the chain \([y]=[r H'/H] = R_*[H'] / H(R_*)\) with the explicit expression of \([H']\) leads to (1).

Although the result is correct, the procedure has two drawbacks. The first comes from a practical point of view. The procedure relies completely on the use of the EFEs for a perfect fluid at both sides (vacuum taken as a trivial particular case). If one needs to consider other matter fields at the interior, or even phase transitions in different regions, the derivation of [y] must be carried out for each different case. Let us stress that after [1, 2] were published, several works on other types of stellar interiors miss the derivation of [y] to properly justify that y is taken to be “continuous".

The second drawback is conceptual, since the procedure also relies on the setting of the interior and exterior problems as one single problem on a common domain, \(r\in (0,\infty )\), and then implicitly assumes that the perturbed metric functions have the continuity properties needed to devise the EFEs in a distributional sense. This setting has its basis in the original Hartle-Thorne perturbative framework [7, 8], where all the perturbed metric functions were assumed to be continuous in that sense. However, the study of matchings in perturbation theory has shown that that construction is not necessary, and not desirable in some cases of interest. In perturbed matching theory, the interior and exterior first order problems (denoted with a \(+\) and − respectively) are more conveniently treated as two separate (gauge field) problems with related boundary data at the common boundary \(r_+=r_-=:R_*\), with basis on a purely geometrical construction. In fact, some of the functions may indeed present jumps, that can be made to vanish by partially fixing the gauges, whereas some others necessarily present jumps in general, as otherwise the setting becomes inconsistent. In particular, the amendment needed to the original Hartle-Thorne model has consequences in the computation of the stellar mass to second order [9].

Although perturbed matching theory may seem to be a mere mathematical artifact, apart from providing firm and rigorous grounds to the results on perturbed matchings based on the Hartle-Thorne framework (after the needed amendments), it provides, on the one hand, full control over the gauges at either side independently (see [10]). This fact is key in the proofs of uniqueness and existence of compact rotating configurations in GR in perturbation theory to second order [11, 12]. On the other hand, the geometrical basis provides a direct way to generalize the derivation, in particular, of [y] to any matter field content, even including different kind of layers and phase transitions.

In this paper we review the matching conditions to first order in perturbation theory (based on the works [9, 12, 13]) aimed at the tidal problem, starting from a pure geometrical setting, and thus ready to be used to obtain the matching conditions for general stellar matter field contents. We take the opportunity to include a formal way of dealing with multiple concentrically distributed regions. To show how to use the conditions, we review the obtaining of the perturbed matching conditions to first order for the tidal problem for perfect fluid stars [3], thus recovering (and putting on firm grounds) the condition (1), and two-fluid superfluid stars [4]. For completeness, we also provide in Sect. 4 the usual procedure to compute the Love number and how the jump [y] enters the calculation.

We include in the following subsection a brief account on the matching in perturbation theory to set the grounds, provide some relevant references, and fix some notation.

1.1 Matching in perturbation theory

In essence, the problem of matching in perturbation theory to first order in General Relativity starts with a set of two spacetimes with boundary \((\mathcal {M}^+,g^+,\Sigma ^+)\) and \((\mathcal {M}^-,g^-,\Sigma ^-)\) that have been matched across \(\Sigma ^+=\Sigma ^-=:\Sigma \) to create a single spacetime \((\mathcal {M},g)\) with two regions, where \(\mathcal {M}=\mathcal {M}^+\cup \mathcal {M}^-\) and g equals \(g^+\) or \(g^-\) on each corresponding region. Each region is now endowed with a symmetric tensor, \(K_1^+\) and \(K_1^-\), which describe the metric perturbation on the corresponding region. The perturbation parameter \(\varepsilon \) is chosen so that the families of metrics \(g_\varepsilon ^\pm :=g^\pm +\varepsilon K_1^\pm \) describe the metric to first order at each region. By taking the metric \(g_\varepsilon \) on \(\mathcal {M}\) defined to be \(g_\varepsilon ^+\) on \(\mathcal {M}^+\) and \(g_\varepsilon ^-\) on \(\mathcal {M}^-\), one can proceed to construct its Riemann tensor \(\textrm{Riem}(g_\varepsilon )\). We say that the two regions of the given background \((\mathcal {M},g)\) perturbed with \(K_1^\pm \) match (to first order) when \(\textrm{Riem}(g_\varepsilon )\) to first order in \(\varepsilon \) can be constructed as a distribution and does not have a Dirac delta term. The general treatment of the matching to first order, explicitly applicable in terms of any gauge, was done in [14] and [15] (see e.g. [16] and [10] regarding treatments in terms of gauge invariants). It was shown that the two perturbed regions match to first order if and only if there exist a couple vectors \(Z_1^\pm \) defined at points on \(\Sigma \) so that a certain set of conditions on \(\Sigma \) are satisfied, which depend on \(\{g^\pm ,K_1^\pm ,Z_1^\pm \}\). We refer to those as the first order perturbed matching conditions, and the normal part of \(Z_1^\pm \) to \(\Sigma \), that we shall denote by \(\Xi _1^\pm \), describe the deformation of \(\Sigma \) (to first order) as seen from each side [13] in terms of the gauges (or class of gauges) chosen.

The second order problem is constructed analogously in terms of an extra symmetric tensor for each region \(K_2^\pm \) to describe the second order perturbations, and the corresponding second order matching conditions (found in [13]) demand the existence of two extra vectors \(Z_2^\pm \) such that a certain set of conditions for \(\{g^\pm ,K_1^\pm ,K_2^\pm ,Z_1^\pm ,Z_2^\pm \}\) on \(\Sigma \) are satisfied.

The particularization to second order stationary and axially symmetric perturbations around static and spherically symmetric backgrounds was performed in [9] (see also [12]). It must be stressed that the perturbation tensor that suits the even-parity tidal problem scenario enters those constructions at second order. The first order matching conditions suitable for the tidal problem correspond to the conditions at second order with a vanishing first order problem in the treatment in [9, 12] (see [3, 4]).

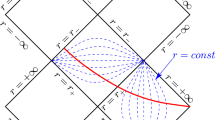
The local nature of the matching procedure allows us to trivially devise the (perturbed) matching procedure needed for a stellar interior made up of layers with different matter contents. For the sake of formality we consider a construction based on a set of \(N+1\) regions \(\{\mathcal {M}_{{(i)}}\}\) with boundary where \(i=1,...,N+1\), so that \(\mathcal {M}_{(1)}\) contains the origin and are ordered from inner to outer, matched together across the matching hypersurfaces \(\Sigma _{{(i)}}\) with \(i=1,\ldots ,N\) to form a global static and spherically symmetric background spacetime as depicted in Fig. 1. Note that one may include \(\Sigma _{(N+1)}\) to denote “infinity”. At any \(\Sigma _{{(i)}}\) separating two regions, say \(\mathcal {M}^+=\mathcal {M}_{_{{(i)}}}\) (inner) and \(\mathcal {M}^-=\mathcal {M}_{{(i+1)}}\) (outer), for any pair of functions \(f^+\) and \(f^-\) defined on the corresponding region, we will use \([f]_i:=f^+|_{\Sigma _{{(i)}}}-f^-|_{\Sigma _{{(i)}}}\) to denote the “jumps” of f there.

Fig. 1
figure 1

Schematic representation of the matching between different manifolds. The i-th manifold \(\mathcal {M}_{{(i)}}\) is matched to \(\mathcal {M}_{{(i+1)}}\) through the hypersurface \(\Sigma _{{(i)}}\). At \(\Sigma _{{(i)}}\) \(\mathcal {M}_{{(i)}}\) plays the role of the inner part of the matching, \(\mathcal {M}^+=\mathcal {M}_{(i)}\), and \(\mathcal {M}_{(i+1)}\) the outer part, so that \(\mathcal {M}^-=\mathcal {M}_{(i+1)}\). The innermost and outermost regions, \(\mathcal {M}_{(1)}\) and \(\mathcal {M}_{(N+1)}\) are not linked to any other spacetime

Full size image

2 Geometrical perturbed matching conditions

In this section we set forth the perturbed matching conditions to first order for static and axially symmetric even parity perturbations around a static and spherically symmetric background at any hypersurface \(\Sigma _{{(i)}}\) in purely geometrical terms. With the tidal problem in mind we restrict the analysis, as usual, to the \(\ell \ge 2\) sector. We refer to [4], based in turn on [12] and [9], for the proving details.

In principle, each \(\mathcal {M}_{{(i)}}\) is endowed with the usual spherical coordinates \(\{t_i,r_i,\theta _i,\phi _i\}\), and we may indicate by \(f_i\) that a function is defined on \(\mathcal {M}_{{(i)}}\). However, to avoid flooding all equations with i indices, in what follows we only show explicitly the i-dependence at the jumps of functions.

2.1 Background

The metric of the background configuration in spherical coordinates is given by

$$\begin{aligned} g=-e^{\nu (r)}\textrm{d}t^2+e^{\lambda (r)}\textrm{d}r^2+r^2(\textrm{d}\theta ^2+\sin ^2\theta \textrm{d}\phi ^2), \end{aligned}$$
(2)

(i-subindexes ommited in the functions and coordinates) on each \(\mathcal {M}_{(i)}\). Given the spherical symmetry of the whole configuration, the matching hypersurfaces \(\Sigma _{{(i)}}\) inherit the symmetries and they can be parametrized by common values of \(\{t,\theta ,\phi \}\) at each side (see e.g. [17]). Then, the matching conditions for the background configuration are \([r]_i=0\), that establishes that \(\Sigma _{(i)}\) is defined by the same value, say \(R_i\), of the respective radial coordinates r, and

$$\begin{aligned}&[\lambda ]_i=0,\quad [\nu ]_i=0,\end{aligned}$$
(3)
$$\begin{aligned}&[\nu ']_i=0. \end{aligned}$$
(4)

Observe that the condition \([\nu ]_i=0\) is, in fact, a consequence of the choice of the t coordinate at each side, which have been taken so that their values coincide on \(\Sigma _{{(i)}}\). It is in that sense that we say that the matching condition just serves to accommodate the choice of “gauges” on each side.

2.2 First order

We take the first order perturbation tensor \(K_1\) describing the static, axially symmetric and even parity tidal field as given in the Regge-Wheeler gauge, and decomposed in Legendre polynomials,

$$\begin{aligned} K_1= \sum _{\ell }\left\{ e^{\nu (r)}H_{0 \ell }(r)\textrm{d}t^2 + e^{\lambda (r)}H_{2 \ell }(r)\textrm{d}r^2+ r^2 K_{\ell }(r)(\textrm{d}\theta ^2 + \sin ^2\theta \textrm{d}\phi ^2)\right\} P_{\ell }(\cos \theta ), \end{aligned}$$
(5)

on each region. The matching conditions for \(\ell \ge 2\) on each \(\Sigma _{(i)}\) read [see Eqs. (37)-(39) in [4]]

$$\begin{aligned}&[K_{\ell }]_i=0,\quad [H_{0\ell }]_i=0, \end{aligned}$$
(6)
$$\begin{aligned}&[H_{2\ell }]_i-{R_i}[K_{\ell }']_i= e^{-\lambda ({R_i})/2}\Xi _{\ell i}[\lambda ']_i,\end{aligned}$$
(7)
$$\begin{aligned}&[H'_{0\ell }]_i+\frac{R_i}{2} \nu '({R_i})[K'_\ell ]_i= -e^{-\lambda ({R_i})/2}\Xi _{\ell i}[\nu '']_i, \end{aligned}$$
(8)

for some functions \(\Xi _{\ell i}\) at each \(\ell \ge 2\). As mentioned in the Introduction, the functions \(\Xi _{\ell i}\) will describe the deformation of the hypersurface \(\Sigma _{(i)}\) in the class of gauges compatible with the problem (and it is equal at both sides) [9, 12]. The first order problems for \(\ell \ge 2\) will then match at \(\Sigma _{(i)}\) if and only if there exists a quantity \(\Xi _{\ell i}\) such that Eqs. (6)-(8) are satisfied.

Although the matching conditions for \(\ell =0,1\) are irrelevant as far as the tidal problem is concerned, they can be obtained from [9] or [12], and find, in particular, that the jumps become arbitrary enough as to accommodate all the gauge freedom left at this point.

2.3 Matching conditions in terms of the Einstein tensor

Our goal now is to express the matching conditions in terms of the Einstein tensor of the background geometry \(G^\alpha {}_\beta := \textrm{Ein}(g)^\alpha {}_\beta \). The only independent and nonzero components satisfy the relations (we drop the r-dependence here, prime denotes derivative with respect to r)

$$\begin{aligned}&\lambda '=+\frac{1-e^\lambda }{r}-r e^\lambda G^t{}_t, \end{aligned}$$
(9)
$$\begin{aligned}&\nu '=-\frac{1-e^\lambda }{r}+r e^\lambda G^r{}_r,\end{aligned}$$
(10)
$$\begin{aligned}&\nu '' = \frac{1}{2r}(\lambda '-\nu ')(2+r\nu ')+2 e^{\lambda } G^\theta {}_\theta , \end{aligned}$$
(11)

on any region \(\mathcal {M}_{{(i)}}\). Computing the jumps of the above relations on any \(\Sigma _{{(i)}}\) yields

$$\begin{aligned}&[\lambda ']_i=-{R_i}e^{\lambda ({R_i})}[G^t{}_t]_i, \end{aligned}$$
(12)
$$\begin{aligned}&[\nu ']_i=+{R_i}e^{\lambda ({R_i})}[G^r{}_r]_i,\end{aligned}$$
(13)
$$\begin{aligned}&[\nu '']_i=\left( 1+\frac{{R_i}\nu '({R_i})}{2}\right) \frac{[\lambda ']_i}{{R_i}}+2 e^{\lambda ({R_i})}[G^\theta {}_\theta ]_i. \end{aligned}$$
(14)

As a result, using also that the mass function is given by

$$\begin{aligned} M(r)=\frac{r}{2}\left( 1-e^{-\lambda (r)}\right) , \end{aligned}$$
(15)

the matching conditions (3)-(4) can be rewritten as

$$\begin{aligned}&[M]_i=0,\quad [\nu ]_i=0, \end{aligned}$$
(16)
$$\begin{aligned}&[G^r{}_r]_i=0, \end{aligned}$$
(17)

while (6)-(8) read

$$\begin{aligned}&[K_{\ell }]_i=0,\quad [H_{0\ell }]_i=0,\end{aligned}$$
(18)
$$\begin{aligned}&[H_{2\ell }]_i-{R_i}[K_{\ell }']_i= -{R_i}e^{\lambda ({R_i})/2}\Xi _{\ell i}[G^t{}_t]_i,\end{aligned}$$
(19)
$$\begin{aligned}&[H'_{0\ell }]_i-[K'_\ell ]_i= -2 e^{\lambda ({R_i})/2} \Xi _{\ell i}[G^\theta {}_\theta ]_i-\left( 1+\frac{{R_i}\nu '({R_i})}{2}\right) \frac{[H_{2\ell }]_i}{{R_i}}. \end{aligned}$$
(20)

3 Application to general relativity

In this section we review how the above construction of the perturbed matching to first order applies to problems in perturbation theory to first order in General Relativity (without cosmological constant) in the present context for the tidal problem, i.e. perturbations of the form (5) around static and spherically symmetric backgrounds. For any general case, anyway, the procedure consists in the three following steps.

  1. (i)

    As a first step, since only the Einstein tensor of the background geometry enters the perturbed matching to first order, it suffices to introduce the Einstein field equations (EFE) at the background level (we omit the i index for each region)

    $$\begin{aligned} G{}^\alpha {}_\beta = \varkappa T{}^\alpha {}_\beta , \end{aligned}$$
    (21)

    in the equations (16)-(20) to obtain the geometrical perturbed matching conditions in terms of quantities related to the desired matter field contents of the model. We are using \(G=\textrm{Ein}(g)\), T for the energy-momentum tensor at the background level, and \(\varkappa \) for the gravitational coupling constant.

  2. (ii)

    The second step consists in using the EFEs at first order, together with the perturbed matching conditions from the first step. This may provide additional conditions on the jumps of the perturbation metric functions \(\{H_{0\ell },H_{2\ell }, K_{\ell }\}\).

  3. (iii)

    The final step corresponds to the addition of the matter field matching conditions governing the behaviour of the matter fields across layers, such as surfaces separating different media, phase transitions, charged surfaces, etc...

Before we start with the first step, observe that the Einstein tensor of the background geometry given by (2) only has (at most) three non-vanishing components \(G^t{}_t\), \(G^r{}_r\), and \(G^\theta {}_\theta =G^\phi {}_\phi \) (in all regions). The form of the energy-momentum tensor compatible with that, c.f. (21), is many times referred to as an “anisotropic fluid” with “radial pressure” \(T^r{}_r=\varkappa ^{-1}G^r{}_r\). Equation (17) thus states that the radial pressure cannot have a jump on any matching hypersurface \(\Sigma _{{(i)}}\). If the outermost region is the exterior vacuum to a compact object, this condition establishes the value \({R_N}\) of the radial coordinate where the boundary common to the two problems is located. On the other hand, notice, however, that neither \([G^\theta {}_\theta ]_{i}\) nor \([G^t{}_t]_{i}\) are necessarily zero in general, and therefore neither are \([T^\theta {}_\theta ]_{i}\) nor \([T^t{}_t]_{i}\). If there are no equations for the matter fields, nor additional field matching conditions for them, the necessary and sufficient conditions for “anisotropic fluids” to match at first order are the background matching equations (16)-(17) plus the two first order conditions in (18). Therefore, in that case, the jumps of \(H_{2\ell }\) and the derivatives of all the perturbation metric functions are not constrained, a priori.

In the following we consider perfect fluid and two-fluid superfluid regions, using steps (i) and (ii) to recover the known matching conditions in the tidal problem for neutron and quark stars (see e.g. [1,2,3]) and superfluid neutron stars (see e.g. [18]).

3.1 Step (i): geometrical perturbed matching conditions using the background field equations

Let us start by performing the first step (i) for perfect fluid and two-fluid regions.

Perfect fluid: To fix some notation, we write the energy-momentum tensor for a perfect fluid as

$$\begin{aligned} T^\alpha {}_{\beta }=(E+P)U^\alpha U_\beta +P \delta ^\alpha _{\beta }, \end{aligned}$$
(22)

for some unit fluid flow U, where E and P are the corresponding energy density and pressure, respectively. Given the form of the Einstein tensor for (2), as mentioned above, the EFEs on the background imply that \(U=e^{-\nu /2}\partial _t\), and require only the equation

$$\begin{aligned} G^r{}_r=G^\theta {}_\theta . \end{aligned}$$
(23)

The energy density and pressure are then given by the relations

$$\begin{aligned} G^t{}_t=-\varkappa E,\quad G^r{}_r(=G^\theta {}_\theta =G^\phi {}_\phi )=\varkappa P. \end{aligned}$$
(24)

The matching conditions (16)-(20) applied to a perfect fluid thus read

$$\begin{aligned}&[M]_i=0,\quad [\nu ]_i=0,\end{aligned}$$
(25)
$$\begin{aligned}&[P]_i=0,\end{aligned}$$
(26)
$$\begin{aligned}&[K_{\ell }]_i=0,\quad [H_{0\ell }]_i=0,\end{aligned}$$
(27)
$$\begin{aligned}&[H_{2\ell }]_i-R_i [K_{\ell }']_i= \varkappa R_i e^{\lambda (R_i)/2}\Xi _{\ell i}[E]_i,\end{aligned}$$
(28)
$$\begin{aligned}&[H'_{0\ell }]_i-[K'_\ell ]_i= -\left( 1+\frac{R_i\nu '(R_i)}{2}\right) \frac{[H_{2\ell }]_i}{R_i}. \end{aligned}$$
(29)

Observe that because of the field equations at the background level, c.f. (23), we now have \([G^\theta {}_\theta ]_i=0\) and therefore (20), that becomes (29), involves perturbation metric functions only.

If the outer region is vacuum, the jump of the energy is simply \([E]_{i=N}=E^+({R_N})\), where \({R_N}\) satisfies \(P^+({R_N})=0\). In general, the values of the energy density at the matching hypersurfaces \(\Sigma _{{(i)}}\), and thus the jumps \([E]_i\), will be determined by the barotropic EOS \(E=E(P)\) that govern the stellar configurations on the different regions. In other cases with no barotropic EOS, such as homogeneous stars [19] and some Skyrme stars [20], those values will be determined by whatever relations used to close the system of equations.

Note that at this point the function \(H_{2\ell }\) may present jumps at the matching hypersurfaces (see (29)). Later we are going to see how the perfect fluid equations at first order (in combination with the rest of conditions) imply the vanishing of those jumps.

Superfluid: For completeness, let us introduce very briefly the two-fluid superfluid formalism, as described in [21] (see also [22]). For brevity, we refer to this formalism simply as superfluid. The flow of neutrons and protons is given by \(n^\alpha =n u^\alpha \) and \(p^\alpha =p v^\alpha \), where n and p are the number densities of neutrons and protons, respectively, and \(u^\alpha \) and \(v^\alpha \) are unit timelike vectors. All the model is determined by the master function

$$\begin{aligned} \Lambda = \Lambda (n^2,p^2,x^2), \end{aligned}$$

where \(n^2:=n_\alpha n^\alpha \), \(p^2:=p_\alpha p^\alpha \), and \(x^2:=-p_\alpha n^\alpha \) is the interaction term. With the help of the definitions

$$\begin{aligned} \mu _{\alpha }:={{\mathcal {B}}}n_{\alpha }+{{\mathcal {A}}}p_{\alpha },\qquad \chi _{\alpha }:={{\mathcal {C}}}p_{\alpha }+{{\mathcal {A}}}n_{\alpha }, \end{aligned}$$

with

$$\begin{aligned} {{\mathcal {A}}}:=-\frac{\partial \Lambda (n^2,p^2,x^2)}{\partial x^2},\quad {{\mathcal {B}}}:=-2\frac{\partial \Lambda (n^2,p^2,x^2)}{\partial n^2},\quad {{\mathcal {C}}}:=-2\frac{\partial \Lambda (n^2,p^2,x^2)}{\partial p^2}, \end{aligned}$$

and

$$\begin{aligned} \Psi :=\Lambda -n^{\alpha }\mu _{\alpha }-p^{\alpha }\chi _{\alpha }, \end{aligned}$$
(30)

the energy-momentum tensor reads

$$\begin{aligned} T^\alpha {}_\beta =\Psi \delta ^\alpha _\beta +p^\alpha \chi _\beta +n^\alpha \mu _\beta . \end{aligned}$$
(31)

Similarly as in the perfect fluid case, staticity and spherical symmetry of the background geometry requires that \(u^\alpha =v^\alpha \). That induces (31) to take the form of a perfect fluid with E replaced by \(-\Lambda \). As a result, for this two-fluid model the perturbed matching conditions are given by the set {(25),(27),(29)} plus

$$\begin{aligned}&[\Psi ]_i=0,\end{aligned}$$
(32)
$$\begin{aligned}&[H_{2\ell }]_i-R_i [K_{\ell }']_i= -\varkappa R_i e^{\lambda (R_i)/2}\Xi _{\ell i}[\Lambda ]_i. \end{aligned}$$
(33)

Now, if the outer region is vacuum, then we have \([\Lambda ]_{i=N}=\Lambda ^+({R_N})\), where \({R_N}\) satisfies \(\Psi ^+({R_N})=0\).

Superfluid and perfect fluid: Some models consider stellar configurations composed of different kinds of fluids. For instance, in [23] a stellar model with a superfluid core and perfect fluid crust is studied. In such case, the same arguments as those above for each side can be used to show that the perturbed matching conditions for an inner superfluid region and an outer perfect fluid region are given by the set {(25),(27),(29)} plus

$$\begin{aligned}&\Psi (R_i)=P(R_i),\end{aligned}$$
(34)
$$\begin{aligned}&[H_{2\ell }]_i-R_i [K_{\ell }']_i=-\varkappa R_i e^{\lambda (R_i)/2}\Xi _{\ell i}\left( \Lambda (R_i)+E(R_i)\right) . \end{aligned}$$
(35)

If the star were composed of an inner perfect fluid and an outer superfluid (even though this might not be physically realistic), Eq. (35) ought to be replaced by the same equation with a change of sign at the right-hand side.

3.2 Step (ii): adding the field equations at first order

Let us recall how the EFEs at first order are derived from \(G_\varepsilon :=\text{ Ein }(g_\varepsilon )\) and some \(\varepsilon \)-family of energy-momentum tensors \(T_{\varepsilon }\) such that \(T_{\varepsilon =0}=T\). It suffices to consider the family of equations \( G_\varepsilon {}^\alpha {}_\beta = \varkappa T_\varepsilon {}^\alpha {}_\beta , \) that reduces to (21) for \(\varepsilon =0\).

The first order equations are thus given by

$$\begin{aligned} G^{(1)}{}^\alpha {}_\beta = \varkappa T^{(1)}{}^\alpha {}_\beta , \end{aligned}$$
(36)

where

$$\begin{aligned} G^{(1)}{}^\alpha {}_\beta =\frac{\partial G_\varepsilon {}^\alpha {}_\beta }{\partial \varepsilon }\bigg |_{\varepsilon =0},\quad T^{(1)}{}^\alpha {}_\beta = \frac{\partial T_\varepsilon {}^\alpha {}_\beta }{\partial \varepsilon }\bigg |_{\varepsilon =0}. \end{aligned}$$

For the perfect fluid, one takes the form \( T_\varepsilon ^\alpha {}_\beta = (E_\varepsilon +P_\varepsilon )U_\varepsilon ^\alpha U_{\varepsilon \beta }+P_\varepsilon \delta ^\alpha _\beta , \) for some vector \(U_\varepsilon \) unit with respect to \(g_\varepsilon \) and such that \(U_{\varepsilon =0}=U\), and corresponding energy density \(E_\varepsilon \) and pressure \(P_\varepsilon \) satisfying \(E_{\varepsilon =0}=E\), \(P_{\varepsilon =0}=P\). If a barotropic EOS is given in the form E(P), then it is imposed that \(E_\varepsilon =E(P_\varepsilon )\). Similarly, for the two fluid one considers \(n_\varepsilon {}^\alpha =n_\varepsilon u_\varepsilon {}^\alpha \), \(p_\varepsilon {}^\alpha =p_\varepsilon v_\varepsilon {}^\alpha \) and, given a ruling master function \(\Lambda (n^2,p^2,x^2)\), takes \(\Lambda _\varepsilon =\Lambda (n_\varepsilon ^2,p_\varepsilon ^2,x_\varepsilon ^2)\) from where the rest of quantities are constructed, following the formalism explained above, to form \( T_\varepsilon {}^\alpha {}_\beta =\Psi _\varepsilon \delta ^\alpha _\beta +p_\varepsilon {}^\alpha \chi _\varepsilon {}_\beta +n_\varepsilon {}^\alpha \mu _\varepsilon {}_\beta . \)

It is well known that given the form of \(K_1\) in (5), and thus of \(g_\varepsilon =g+\varepsilon K_1\), the resulting \(G^{(1)}\) takes a form so that the equations (36) in both the perfect fluid and two-fluid cases for \(\ell \ge 2\) yield [24, 25]

$$\begin{aligned}&H_2{}_\ell =H_0{}_\ell , \end{aligned}$$
(37)
$$\begin{aligned}&K_\ell {}' = H_0{}_\ell '+ \nu {}' H_0{}_\ell ,\end{aligned}$$
(38)
$$\begin{aligned}&r^2 \nu {}' H_0{}_\ell ' = e^{\lambda } \left( \ell (\ell +1) -2 \right) K_\ell + \left( r (\lambda {}'+\nu {}') - \left( r \nu {}'\right) ^2 -e^{\lambda } \ell (\ell +1) + 2 \right) H_0{}_\ell , \end{aligned}$$
(39)

plus relations that involve the first order quantities relative to the matter fluids.

We can now take differences of these equations at either side of the matching hypersurfaces \(\Sigma _{{(i)}}\) and thus obtain relations between the jumps of the perturbation metric functions. The task is then to combine the perturbed matching conditions we already have with those relations.

Perfect fluid: The combination of the set of equations (25)-(29) with the differences of (37)-(39), using the relations in (9)-(11), is equivalent to the set of equations [3]

$$\begin{aligned}&[M]_i=0,\quad [\nu ]_i=0,\end{aligned}$$
(40)
$$\begin{aligned}&[P]_i=0, \end{aligned}$$
(41)
$$\begin{aligned}&[H_{0\ell }]_i=0,\quad [H_{2\ell }]_i=0,\quad [K_\ell ]_i=0, \end{aligned}$$
(42)
$$\begin{aligned}&[H'_{0\ell }]_i=[K'_\ell ]_i=\frac{\varkappa e^{\lambda (R_i)}}{\nu '(R_i)}H_{0\ell }(R_i)[E]_i,\end{aligned}$$
(43)
$$\begin{aligned}&[E]_i\left( \Xi _{\ell i}+\frac{e^{\lambda (R_i)/2}}{\nu '(R_i)}H_{0\ell }(R_i)\right) =0, \end{aligned}$$
(44)

for \(\ell \ge 2\).

Two comments are in order. First, these matching conditions, for \(\ell \ge 2\), appeared already (without proof) in an analogous context in Appendix B in [26]. There, the matching to all \(\ell \) is included, although the “continuity" of the \(\ell =0,1\) sector may need some partial gauge fixing [9, 12]. Second, it must be stressed that the background matching conditions (40) and (41), together with the “continuity" conditions (42), plus the field equations (38) and (39) guarantee that the matching condition (43) is satisfied. This fact, which was also already observed in [26], is the reason why the discontinuity of \([H_0']\) can be found using the EFEs provided that the functions involved are asummed to be continuous.

Superfluid: For the two-fluid model it is easy to see that it suffices to replace E with \(-\Lambda \) and P with \(\Psi \) in (32) and (33). As a result, the full set of perturbed matching conditions to first order in this case is given by (40), (42) plus

$$\begin{aligned}&[\Psi ]_i=0,\end{aligned}$$
(45)
$$\begin{aligned}&[H'_{0\ell }]_i=[K'_\ell ]_i=-\frac{\varkappa e^{\lambda (R_i)}}{\nu '(R_i)}H_{0\ell }(R_i)[\Lambda ]_i,\end{aligned}$$
(46)
$$\begin{aligned}&[\Lambda ]_i\left( \Xi _{\ell i}+\frac{e^{\lambda (R_i)/2}}{\nu '(R_i)}H_{0\ell }(R_i)\right) =0, \end{aligned}$$
(47)

for \(\ell \ge 2\).

Superfluid and perfect fluid: Likewise, for an inner superfluid model matching to an outer perfect fluid, the set is given by (40), (42) plus

$$\begin{aligned}&\Psi (R_i)=P(R_i),\end{aligned}$$
(48)
$$\begin{aligned}&[H'_{0\ell }]_i=[K'_\ell ]_i=-\frac{\varkappa e^{\lambda (R_i)}}{\nu '(R_i)}H_{0\ell }(R_i)\left( \Lambda (R_i)+E(R_i)\right) ,\end{aligned}$$
(49)
$$\begin{aligned}&\left( \Lambda (R_i)+E(R_i)\right) \left( \Xi _{\ell i}+\frac{e^{\lambda (R_i)/2}}{\nu '(R_i)}H_{0\ell }(R_i)\right) =0, \end{aligned}$$
(50)

for \(\ell \ge 2\).

Clearly, the same equations with a change of sign in E and \(\Lambda \) hold if the inner region is a perfect fluid and the outer region is the superfluid.

4 Tidal problem and Love number

The Love number at each harmonic \(\ell \) is obtained from the function \(H_{0\ell }\) and its radial derivative \(H'_{0\ell }\) evaluated at the outermost boundary of the star in the vacuum exterior, that we denote by \(\mathcal {M}^-\) with relative quantities also tagged with the minus sign. In the present setting and notation, that is \(H^-_{0\ell }({R_N})\) and \(H'{}^-_{0\ell }({R_N})\). The solution \(H_{0\ell }\) of the equations (38)-(39) for a vacuum region are the associated Legendre functions \(P_\ell ^n\), \(Q_\ell ^n\) with \(n = 2\)

$$\begin{aligned} H_{0\ell }^-(r_-)=a_{\ell P}{\hat{P}}_{\ell }^2\left( \frac{r_-}{M}-1\right) +a_{\ell Q}{\hat{Q}}_{\ell }^2\left( \frac{r_-}{M}-1\right) , \end{aligned}$$
(51)

where the Legendre functions have been normalized so that \({\hat{P}}_\ell ^2(x)\simeq x^{\ell }\) and \({\hat{Q}}_\ell ^2(x)\simeq 1/x^{\ell +1}\) when \(x\rightarrow \infty \), and are given by

$$\begin{aligned} {\hat{P}}_{\ell }^2(x):=\left( \frac{2^\ell }{\sqrt{\pi }}\frac{\Gamma (\ell +1/2)}{\Gamma (\ell -1)}\right) ^{-1} P_{\ell }^2(x),\\ {\hat{Q}}_{\ell }^2(x):=\left( \frac{\sqrt{\pi }}{2^{\ell +1}}\frac{\Gamma (\ell +3)}{\Gamma (\ell +3/2)}\right) ^{-1} Q_{\ell }^2(x). \end{aligned}$$

The Love number is defined as

$$\begin{aligned} k_\ell :=\frac{1}{2}\left( \frac{M}{{R_N}}\right) ^{2\ell +1}a_\ell , \end{aligned}$$
(52)

where M is the mass of the star \(M=M({R_N})\) (observe the mass function has no jumps, c.f. (40)), and \(a_\ell \) is the ratio between the two constants in (51)

$$\begin{aligned} a_\ell :=\frac{a_{\ell Q}}{a_{\ell P}}=-\frac{\partial _{r_-} {\hat{P}}_\ell ^2-(y_\ell ^-/{R_N}){\hat{P}}_\ell ^2}{\partial _{r_-} {\hat{Q}}_\ell ^2-(y_\ell ^-/{R_N}){\hat{Q}}_\ell ^2}\bigg |_{r_-={R_N}}, \end{aligned}$$
(53)

where \(y_\ell :=rH_{0\ell }'/H_{0\ell }\). The leading order Love number, \(k_2\), is many times replaced (but often called also Love number) by the tidal deformability \(\lambda _2=a_2/3\).

Computationally, one must fix some boundary conditions at the origin and integrate the EFE from \(\mathcal {M}_{(1)}\) to \(\mathcal {M}_{(N)}\), respecting the matching conditions at each boundary, until reaching the outermost boundary, \(\Sigma _{(N)}\). Once the interior problem has been solved (and thus \(y_\ell ^+({R_N})\) is known), the value of \(y_\ell ^-\) at the boundary, \(y_\ell ^-({R_N})\), has to be obtained from the matching of the two regions,

$$\begin{aligned} y_\ell ^-({R_N})=y_\ell ^+({R_N})-[y_\ell ]_N \end{aligned}$$

with

$$\begin{aligned}{}[y_\ell ]_N=\left[ \frac{r H_{0\ell }'}{H_{0\ell }}\right] _N =\frac{{R_N}}{H_{0\ell }({R_N})}\left[ H'_{0\ell }\right] _N, \end{aligned}$$
(54)

after using \([H_{0\ell }]_N=0\) in the last equality. Then, using (53) the tidal deformability, \(\lambda _2\) (and the Love number \(k_2\) using also (52)) is computed.

Perfect fluid: For the perfect fluid case, using equations (42) and (43), together with the vacuum solutions of \(\lambda (r)\) and \(\nu (r)\),

$$\begin{aligned} e^{-\lambda (r)}=e^{\nu (r)}=1-\frac{2M}{r}, \end{aligned}$$
(55)

equation (54) reads

$$\begin{aligned}{}[y_\ell ]_N=\varkappa \frac{{R_N}^3}{2M}E({R_N}), \end{aligned}$$
(56)

thus recovering (1) for \(\ell =2\) after denoting \({R_N}=R_*\). Then,

$$\begin{aligned} a_\ell =-\frac{\partial _{r_+} {\hat{P}}_\ell ^2-(y_\ell ^+/{R_N}){\hat{P}}_\ell ^2+(\varkappa {R_N}^2 E({R_N})/2M){\hat{P}}_\ell ^2}{\partial _{r_+} {\hat{Q}}_\ell ^2-(y_\ell ^+/{R_N}){\hat{Q}}_\ell ^2+(\varkappa {R_N}^2 E({R_N})/2M){\hat{Q}}_\ell ^2}\bigg |_{r_+={R_N}}, \end{aligned}$$
(57)

where we have recovered the \(+\) index in \(y_\ell ^+\) because \(y_\ell ^+\ne y_\ell ^-\) in general.

Superfluid: For the superfluid case, the analogous procedure shows that it suffices to replace E by \(-\Lambda \), so that [4]

$$\begin{aligned}{}[y_\ell ]_N=-\varkappa \frac{{R_N}^3}{2 M}\Lambda ({R_N}), \end{aligned}$$
(58)

and

$$\begin{aligned} a_\ell&=-\frac{\partial _{r_+} {\hat{P}}_\ell ^2-(y_\ell ^+/{R_N}){\hat{P}}_\ell ^2-(\varkappa {R_N}^2\Lambda ({R_N})/2M){\hat{P}}_\ell ^2}{\partial _{r_+} {\hat{Q}}_\ell ^2-(y_\ell ^+/{R_N}){\hat{Q}}_\ell ^2-(\varkappa {R_N}^2\Lambda ({R_N})/2M){\hat{Q}}_\ell ^2}\bigg |_{r_+={R_N}}. \end{aligned}$$
(59)

5 Conclusions

The set of geometrical matching conditions reviewed in this article serves as a basis for those works that aim to study the tidal problem for non perfect fluid stellar configurations for which Eq. (15) in [2] no longer applies as such. In this regard, although equations to first order for perfect fluid and superfluid interiors appear to be analogous (in the matching conditions it is just a change \(E\rightarrow -\Lambda \) and \(P\rightarrow \Psi \)), at second order this similarity is completely lost; compare, for instance, the contribution of the mass at second order, \(\delta M\), from Eq. (103) in [9] with that of Eq. (97) in [18].

Even though we have restricted ourselves to the theory of General Relativity using the Einstein field equations at some point, due to the geometrical nature of (16)-(20), which are a consequence of imposing that the Riemann tensor has no Dirac delta terms, these equations may still hold as a minimum set of matching conditions on alternative metric theories of gravity, as well as metric-affine theories (except for one very particular case, see [27]). In those alternative theories one would expect to need more conditions, as it happens when dealing with quadratic theories of gravity, see e.g. [28] and references therein. Let us stress finally that the geometrical procedure in Sec. 2 is suited to be applied to any stellar exterior, that is, regardless of whether the “vacuum" exterior of some given theory is or is not Schwarzschild, see e.g. [29].