Abstract
This work seeks to make explicit the operational connection between the preparation of two-level quantum systems with their corresponding description (as states) in a Hilbert space. This may sound outdated, but we show there is more to this connection than common sense may lead us to believe. To bridge these two separated realms—the actual laboratory and the space of states—we rely on a paradigmatic mathematical object: the Hopf fibration. We illustrate how this connection works in practice with a simple optical setup. Remarkably, this optical setup also reflects the necessity of using two charts to cover a sphere. Put another way, our experimental realization reflects the bi-dimensionality of a sphere seen as a smooth manifold.


Similar content being viewed by others
Data Availability
No datasets were generated or analysed during the current study.
Notes
The details of some set theory concepts and action of groups on the latter are presented in the Appendix 1.
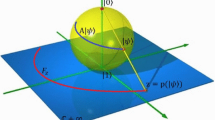
The motivation for such choice stems from the fact that any direction in the three-dimensional space \(\mathbb {R}^3\) can be defined uniquely by the two angles \(\theta\) and \(\varphi\). Thus, by fixing \(\xi =0\), we are left with two parameters, \(\eta\) and \(\zeta\), to be identified in one way or the other with \(\theta\) and \(\varphi\).
References
A. Peres, Quantum theory: concepts and methods, nachdr. edn. No. vol. 72 in Fundamental theories of physics (Kluwer Acad. Publ, Dordrecht, 2010)
M.S. Leifer, R.W. Spekkens, Towards a formulation of quantum theory as a causally neutral theory of Bayesian inference. Phys. Rev. A 88, 052130 (2013). https://doi.org/10.1103/PhysRevA.88.052130
M. Leifer, Is the quantum state real? an extended review of psi-ontology theorems. Quanta 3(1), 67–155 (2014). https://doi.org/10.12743/quanta.v3i1.22
R. Colbeck, R. Renner, No extension of quantum theory can have improved predictive power. Nat. Commun. 2(1), 411 (2011). https://doi.org/10.1038/ncomms1416
Y. Aharonov, S. Popescu, D. Rohrlich, P. Skrzypczyk, Quantum cheshire cats. New J. Phys. 15(11), 113015 (2013). https://doi.org/10.1088/1367-2630/15/11/113015
S. Vineberg, In The Stanford encyclopedia of philosophy, ed. by E.N. Zalta, spring 2016 edn. (Metaphysics Research Lab, Stanford University, 2016)
J.G. Kemeny, Fair bets and inductive probabilities. J. Symb. Log. 20(3), 263–273 (1955). https://doi.org/10.2307/2268222
F.J. Anscombe, R.J. Aumann, A definition of subjective probability. Ann. Math. Stat. 34(1), 199–205 (1963). https://doi.org/10.1214/aoms/1177704255
L.J. Savage, The foundations of statistics (Wiley Publications in Statistics, 1954)
B. de Finetti, Theory of probability: a critical introductory treatment (Wiley, 1979)
J.V. Neumann, O. Morgenstern, Theory of games and economic behavior (Princeton University Press, Princeton, NJ, USA, 1944)
R. Simon, N. Mukunda, Universal su(2) gadget for polarization optics. Phys. Lett. A 138(9), 474–480 (1989). https://doi.org/10.1016/0375-9601(89)90748-2
I. Bengtsson, K. Życzkowski, Geometry of quantum states: an introduction to quantum entanglement, second, edition. (Cambridge University Press, Cambridge, 2017)
G.F. Vasconcelos Júnior, R.P.S. Costa, B.F. Rizzuti, Grandezas físicas unidimensionais. Revista Brasileira de Ensino de Física 40(3) (2018). 10.1590/1806-9126-rbef-2017-0289
L. Gaio, D.D. Barros, B. Rizzuti, Grandezas físicas multidimensionais. Revista Brasileira de Ensino de Física 41(3), e20180295 (2019). https://doi.org/10.1590/1806-9126-rbef-2018-0295
B.F. Rizzuti, L.M. Gaio, C. Duarte, Operational approach to the topological structure of the physical space. Found. Sci. 25(3), 711–735 (2020). https://doi.org/10.1007/s10699-020-09650-8
B.F. Rizzuti, L.M. Gaio, L.T. Cardoso, Is time the real line? Found. Phys. 52(5), 105 (2022). https://doi.org/10.1007/s10701-022-00623-4
M.A. Nielsen, I.L. Chuang, Quantum computation and quantum information, 10th edn. (Cambridge University Press, Cambridge; New York, 2010)
R. Simon, N. Mukunda, Hamilton’s turn and geometric phase for two-level systems. J. Phys. A: Math. Gen. 25(22), 6135–6144 (1992). https://doi.org/10.1088/0305-4470/25/22/034
F.T. Arecchi, E. Courtens, R. Gilmore, H. Thomas, Atomic coherent states in quantum optics. Phys. Rev. A 6(6), 2211–2237 (1972). https://doi.org/10.1103/PhysRevA.6.2211
R. Grossi, L.L. Brugger, B. Rizzuti, C. Duarte, One hundred years later: Stern-Gerlach experiment and dimension witnesses. Revista Brasileira de Ensino de Física 45, e20220227 (2023). https://doi.org/10.1590/1806-9126-rbef-2022-0227
J.R. Munkres, Topology; a first course (Prentice-Hall, Englewood Cliffs, N.J., 1974)
J.M. Jauch, Foundations of quantum mechanics, 2nd edn. Addison-Wesley series in advanced physics (Addison-Wesley, Reading, Mass., 1973)
A.M. Childs, I.L. Chuang, Universal quantum computation with two-level trapped ions. Phys. Rev. A 63(1), 012306 (2000). https://doi.org/10.1103/PhysRevA.63.012306
S.P. Harvey, in Oxford Research Encyclopedia of Physics (Oxford University Press, 2022). https://doi.org/10.1093/acrefore/9780190871994.013.83
W. Unrau, D. Bimberg, Flying qubits and entangled photons: flying qubits and entangled photons. Laser & Photonics Reviews 8(2), 276–290 (2014). https://doi.org/10.1002/lpor.201300050
B. Hensen, H. Bernien, A.E. Dréau, A. Reiserer, N. Kalb, M.S. Blok, J. Ruitenberg, R.F.L. Vermeulen, R.N. Schouten, C. Abellán, W. Amaya, V. Pruneri, M.W. Mitchell, M. Markham, D.J. Twitchen, D. Elkouss, S. Wehner, T.H. Taminiau, R. Hanson, Loophole-free bell inequality violation using electron spins separated by 1.3 kilometres. Nature 526(7575), 682–686 (2015). https://doi.org/10.1038/nature15759
C.H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres, W.K. Wootters, Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 70, 1895–1899 (1993). https://doi.org/10.1103/PhysRevLett.70.1895
S. Walborn, C. Monken, S. Pádua, P. Souto Ribeiro, Spatial correlations in parametric down-conversion. Physics Reports 495(4–5), 87–139 (2010). https://doi.org/10.1016/j.physrep.2010.06.003
C.H. Bennett, G. Brassard, Quantum cryptography: public key distribution and coin tossing. Theoret. Comput. Sci. 560, 7–11 (2014). https://doi.org/10.1016/j.tcs.2014.05.025
A.K. Ekert, Quantum cryptography based on bell’s theorem. Phys. Rev. Lett. 67, 661–663 (1991). https://doi.org/10.1103/PhysRevLett.67.661
F. Arute, K. Arya, R. Babbush, D. Bacon, J.C. Bardin, R. Barends, R. Biswas, S. Boixo, F.G.S.L. Brandao, D.A. Buell, B. Burkett, Y. Chen, Z. Chen, B. Chiaro, R. Collins, W. Courtney, A. Dunsworth, E. Farhi, B. Foxen, A. Fowler, C. Gidney, M. Giustina, R. Graff, K. Guerin, S. Habegger, M.P. Harrigan, M.J. Hartmann, A. Ho, M. Hoffmann, T. Huang, T.S. Humble, S.V. Isakov, E. Jeffrey, Z. Jiang, D. Kafri, K. Kechedzhi, J. Kelly, P.V. Klimov, S. Knysh, A. Korotkov, F. Kostritsa, D. Landhuis, M. Lindmark, E. Lucero, D. Lyakh, S. Mandrá, J.R. McClean, M. McEwen, A. Megrant, X. Mi, K. Michielsen, M. Mohseni, J. Mutus, O. Naaman, M. Neeley, C. Neill, M.Y. Niu, E. Ostby, A. Petukhov, J.C. Platt, C. Quintana, E.G. Rieffel, P. Roushan, N.C. Rubin, D. Sank, K.J. Satzinger, V. Smelyanskiy, K.J. Sung, M.D. Trevithick, A. Vainsencher, B. Villalonga, T. White, Z.J. Yao, P. Yeh, A. Zalcman, H. Neven, J.M. Martinis, Quantum supremacy using a programmable superconducting processor. Nature 574(7779), 505–510 (2019). https://doi.org/10.1038/s41586-019-1666-5
A. Acín, L. Masanes, Certified randomness in quantum physics. Nature 540(7632), 213–219 (2016). https://doi.org/10.1038/nature20119
R.D. Somma, S. Boixo, H. Barnum, E. Knill, Quantum simulations of classical annealing processes. Phys. Rev. Lett. 101, 130504 (2008). https://doi.org/10.1103/PhysRevLett.101.130504
F.G. Brandao, K.M. Svore, In 2017 IEEE 58th annual symposium on foundations of computer science (FOCS) (IEEE, Berkeley, CA, 2017), p. 415–426. https://doi.org/10.1109/FOCS.2017.45
O. Stern, Ein Weg zur experimentellen Prüfung der Richtungsquantelung im Magnetfeld. Z. Phys. 7(1), 249–253 (1921). https://doi.org/10.1007/BF01332793
W. Gerlach, O. Stern, Der experimentelle Nachweis des magnetischen Moments des Silberatoms. Z. Phys. 8(1), 110–111 (1921). https://doi.org/10.1007/BF01329580
W. Gerlach, O. Stern, Der experimentelle Nachweis der Richtungsquantelung im Magnetfeld. Z. Phys. 9(1), 349–352 (1922). https://doi.org/10.1007/BF01326983
W. Gerlach, O. Stern, Das magnetische Moment des Silberatoms. Z. Phys. 9(1), 353–355 (1922). https://doi.org/10.1007/BF01326984
M. Nakahara, Geometry, topology, and physics. Graduate student series in physics (A. Hilger, Bristol, England ; New York, 1990)
A.S. de Carvalho, R.M. Siejakowski, Topologia e geometria de 3-variedades, uma agradável introdução (Editora do IMPA, Rio de Janeiro, Brasil, 2021)
P.A.M. Dirac, The principles of quantum mechanics, 4th edn. No. 27 in International series of monographs on physics (Clarendon Press, Oxford University Press, Oxford, 2010)
W.K. Tung, Group theory in physics (World Scientific, Philadelphia, 1985)
R. Mosseri, R. Dandoloff, Geometry of entangled states, Bloch spheres and Hopf fibrations. Journal of Physics A: Mathematical and General 34(47), 10,243–10,252 (2001). ArXiv:quant-ph/0108137. https://doi.org/10.1088/0305-4470/34/47/324
R. Mosseri, Two and three qubits geometry and hopf fibrations. ArXiv (2003). https://doi.org/10.48550/arXiv.quant-ph/0310053
L. Hardy. Quantum theory from five reasonable axioms (2001)
B. Dakic, C. Brukner. Quantum theory and beyond: is entanglement special? (2009)
L. Masanes, M.P. Müller, A derivation of quantum theory from physical requirements. New J. Phys. 13(6), 063001 (2011). https://doi.org/10.1088/1367-2630/13/6/063001
G. Chiribella, G.M. D’Ariano, P. Perinotti, Informational derivation of quantum theory. Phys. Rev. A 84(1), 012311 (2011). https://doi.org/10.1103/PhysRevA.84.012311
I. Bengtsson, J. Brännlund, K. Życzkowski, CP\(^{\text{n}}\), or, entanglement illustrated. Int. J. Mod. Phys. A 17(31), 4675–4695 (2002). https://doi.org/10.1142/S0217751X02010820
Acknowledgements
BFR and VGV are in debt with Prof. Wallon A. T. Nogueira, Profa. Giovana Trevisan Nogueira and Prof. Rodrigo A. Dias for helpful discussions and recommendations for completing this work. CD wishes to thank the hospitality of both the Universidade Federal de Pernambuco and the Universidade Federal de Juiz de Fora, where part of this work was realized. LLB would like to express his gratitude to the Universidade Federal de Juiz de Fora and Programa de Bolsas de Pós-Graduação - Física, for his master’s scholarship.
Funding
This work has also been supported by Programa Institucional de Bolsas de Iniciação Científica - VI VIC/Universidade Federal de Juiz de Fora - 2022/2023, project number 51268.
Author information
Authors and Affiliations
Contributions
B. F. Rizzuti proposed the main idea of the manuscript. B. F. Rizzuti and C. Duarte wrote the main manuscript. L. L. Brugger and V. G. Valle prepared Figs. 1-2. B.F.Rizzuti wrote the Appendix 1. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix 1. Basic Set Theory and the Action of Groups on Arbitrary Sets
Appendix 1. Basic Set Theory and the Action of Groups on Arbitrary Sets
In this appendix, we briefly introduce a selection of topics concerning set theory: equivalence relations, equivalence classes, the action of a group on a set and related concepts. Although the points we address here are not new, our intention is to make the manuscript as self-consistent as possible. For an in-depth description, we direct the reader to [23, 40].
We start our overview by reviewing an alternative way of turning elements of a set into equivalent elements. Presumably, the first and foremost notion of equivalence is the one commonly connected with the concept of equality. Disguised by common sense, equality is a binary relation-a relation between two objects-which is reflexive (an object is equal to itself), symmetric (if an object is equal to another, then the latter is also equal to the former), and transitive (if an object is equal to a second, and this second to a third, then the original and the final objects also are so). What is crucial here is that equality, as we know it, is only a special case of a larger class of binary relations intended to capture and classify distinctive characteristics of a collection of objects. The next definitions rigorously address these points.
Definition 1
(Equivalence Relations). Let \(\mathbb {X}\) be a non-empty set and \(\sim \subset \mathbb {X} \times \mathbb {X}\) a relation. We say that \(\sim\) is an equivalence relation whenever the three properties below hold true,
-
i.
\(\sim\) is reflexive: \(x \sim x\), \(\forall x \in \mathbb {X}\).
-
ii.
\(\sim\) is symmetric: \(x \sim y \Rightarrow y \sim x\), \(\forall x,y \in \mathbb {X}\)
-
iii.
\(\sim\) is transitive: if \(x \sim y\) and \(y \sim z\), then \(x \sim z\), \(\forall x,y,z \in \mathbb {X}\).
Remark
Any relation over a given set \(\mathbb {X}\) is a subset R of \(\mathbb {X} \times \mathbb {X}\). In this sense, R is a collection of ordered pairs (x, y) where \(x,y \in \mathbb {X}\). Mainly because we want to express the relational aspect of R and also retain the parallel with the notion of equality, it is usual to write xRy instead of \((x,y) \in R\)-the reader will certainly appreciate this change in notation.
Definition 2
(Equivalence Classes). Let \(\sim\) be an equivalence relation over \(\mathbb {X}\). Given an element y we define the following subsets of \(\mathbb {X}\),
Because \(y \sim y\), \(y \in [y]\), for all elements of \(\mathbb {X}\). Thus, these subsets are well-defined and we name them equivalence classes. In particular, for a given \(y \in \mathbb {X}\), the subset [y] is called the equivalence class of y.
One of the main consequences of establishing an equivalence relation on a set resides in the theorem below. It guarantees that equivalence classes provide a partition of the set they are defined over—that is, a cover of the entire set formed by disjoint subsets.
Theorem 1
(Partition via Equivalence Classes). If \(\sim\) is an equivalence relation on \(\mathbb {X}\), then
Remark
A useful notation to the disjoint union in Eq. (30) is \(\mathbb {X}/\sim\), as it denotes that the set has been partitioned across the many equivalence classes defined by the equivalence relation. For both an intuitive interpretation and formal demonstration, we direct the reader to [14].
Now we turn our attention to group actions on sets. Following the natural steps of introducing sets and relations, we could start with functions (or mappings), which are a special type of relation. However, we would like to do so bearing in mind that the elements of the set should transform guided by a group structure, retaining not only the symmetry properties but also the special transformations the latter usually conveys. Hence, we define the
Definition 3
(Action of a Group). Let \(\mathcal {G}\) be a group and \(\mathbb {X}\) be a non-empty set. The action of \(\mathcal {G}\) on \(\mathbb {X}\) is a map \(\varphi : \mathcal {G} \times \mathbb {X} \rightarrow \mathbb {X}\), satisfying the following conditions,
-
i.
\(\varphi (e,x) = x\), \(\forall \,\, x \in \mathbb {X}\), where e stands for the group identity element.
-
ii.
For each \(g \in \mathcal {G}\), \(\varphi (g, \cdot ): \mathbb {X} \rightarrow \mathbb {X}\) is a bijection.
-
iii.
\(\varphi (g_1, \varphi (g_2,x))=\varphi (g_1g_2,x)\), \(\forall \,\, x \in \mathbb {x}\) and \(\forall \,\, g_1, g_2 \in \mathcal {G}\).
Now, in \(\mathbb {X}\times \mathbb {X}\) we introduce the following relation,
We affirm that \(\sim\) is an equivalence relation. In fact, \(\sim\) is reflexive because i: \(\varphi (e,x) = x\). The symmetry comes from
Finally, the transitivity can also be promptly deduced. It suffices to note that if \(y = \varphi (g_1,x)\) and \(z = \varphi (g_2,y)\), then \(z = \varphi (g_3,x)\), where \(g_3 = g_2 g_1\).
With the equivalence relation defined by the action, we define the equivalence classes by
Due to its special role, an equivalence class of such type is called an orbit through x.
Crucially, according to the theorem 1 above, \(\mathbb {X}\) is partitioned by its disjoint orbits. All in all, that is to say, starting from the action of a group over a set, we can partition that set across the orbits of each of its elements.
Next, we will present some examples of interest not only to our previous discussion per se but also to quantum mechanics in general.
Example 1
For our first example, we consider \(\mathbb {X} = \mathbb {C}^2\) and \(\mathcal {G} = \mathcal {U}(1) = \{ e^{i \alpha } \, \, \alpha \in \mathbb {R} \}\). Define the map
To check that \(\varphi\) is indeed an action, we have
-
i.
\(\mathcal {U}(1) \ni e =1 \Rightarrow \varphi (e, | \psi \rangle ) = | \psi \rangle\).
-
ii.
Given \(\alpha \in \mathbb {R}\), \(\varphi (e^{i \alpha }, \cdot ): \mathbb {C}^2 \rightarrow \mathbb {C}^2\) is a bijection. In effect,
$$e^{i \alpha } | \psi _1 \rangle = e^{i \alpha } | \psi _2 \rangle \Rightarrow | \psi _1 \rangle = | \psi _2 \rangle$$which guarantees that the map is injective. In turn, we point out that any \(| \psi \rangle \in \mathbb {C}^2\) is reached by \(e^{-i\alpha }| \psi \rangle\) under \(\varphi (e^{i \alpha }, \cdot )\). Thus, the map is surjective as well.
-
iii.
At last,
$$\begin{aligned} \varphi (e^{i \alpha _1},e^{i \alpha _2} | \psi \rangle ) = e^{i(\alpha _1+ \alpha _2)}| \psi \rangle = \varphi (e^{i \alpha _1}e^{i \alpha _2}, | \psi \rangle ), \end{aligned}$$which concludes the proof.
The importance of the case in point lies on the fact that the orbits consists of indistinguishable states for two-level quantum systems as well as fibers in the Hopf fibration, as previously discussed in Section 3.
Example 2
Our second example is given by \(\mathbb {X}= \mathbb {R}^n\) and \(\mathcal {G} = \mathbb {R}^* = \mathbb {R}\smallsetminus \{0 \}\), where the group product is the usual multiplication of non-zero real numbers. Define
It is not difficult to conclude that \(\varphi\) is an action. In fact, we have,
-
i.
\(\mathbb {R}^* \ni e = 1 \Rightarrow \varphi (1,\vec {v}) = \vec {v}\).
-
ii.
Given \(\lambda \in \mathbb {R}^*\), \(\varphi (\lambda , \cdot )\) is a bijection for
$$\begin{aligned} \lambda \vec {v}_1=\lambda \vec {v}_2 \Rightarrow \vec {v}_1=\vec {v}_2, \end{aligned}$$which shows the injection. Moreover, any \(\vec {v} \in \mathbb {R}^n\) can be obtained by applying \(\varphi (\lambda , \cdot )\) to \(\lambda ^{-1}\vec {v}\). Hence, the map is also surjective.
-
iii.
Finally, \(\varphi (\lambda _1, \lambda _2 \vec {v}) = \varphi (\lambda _1 \lambda _2 \vec {v})\).
The classes, or orbits, here are straight lines crossing the origin, although \(\vec {0} \ne [\vec {V}]\), for every non-zero vector \(\vec {v}\) in \(\mathbb {R}^n\). Their union forms what is called the projective space, named \(\mathbb {R}\mathbb {P}^{n-1}\). The generalization for \(\mathbb {C}^n\) and, accordingly, to \(\mathbb {C}\mathbb {P}^{n-1}\) is straightforward. The value of the latter to quantum mechanics stems from its intrinsic connection to entanglement [50].
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Valle, V.G., Brugger, L.L., Rizzuti, B.F. et al. Towards Establishing a Connection Between Two-Level Quantum Systems and Physical Spaces. Braz J Phys 54, 93 (2024). https://doi.org/10.1007/s13538-024-01462-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13538-024-01462-6