Let 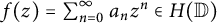$f(z)=\sum _{n=0}^{\infty }a_n z^n \in H(\mathbb {D})$ be an analytic function over the unit disk in the complex plane, and let 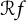$\mathcal {R} f$ be its randomization: 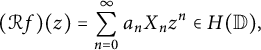$$ \begin{align*}(\mathcal{R} f)(z)= \sum_{n=0}^{\infty} a_n X_n z^n \in H(\mathbb{D}),\end{align*} $$

where 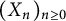$(X_n)_{n\ge 0}$ is a standard sequence of independent Bernoulli, Steinhaus, or Gaussian random variables. In this note, we characterize those 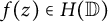$f(z) \in H(\mathbb {D})$ such that the zero set of 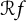$\mathcal {R} f$ satisfies a Blaschke-type condition almost surely: 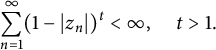$$ \begin{align*}\sum_{n=1}^{\infty}(1-|z_n|)^t<\infty, \quad t>1.\end{align*} $$

设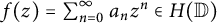$f(z)=\sum _{n=0}^{\infty }a_n z^n \in H(\mathbb {D})$为复平面上单位圆盘上的解析函数，并令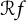$\mathcal {R} f$为其随机化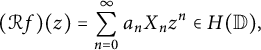：$$ \begin{align*}(\mathcal{R} f)(z)= \sum_{n=0}^{\infty} a_n X_n z^n \在 H(\mathbb{D}),\end{对齐*} $$

其中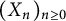$(X_n)_{n\ge 0}$是独立伯努利、斯坦豪斯或高斯随机变量的标准序列。在本文中，我们描述了那些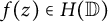$f(z) \in H(\mathbb {D})$，使得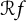$\mathcal {R} f$的零集几乎肯定满足 Blaschke 型条件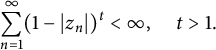：$$ \begin {align*}\sum_{n=1}^{\infty}(1-|z_n|)^t<\infty, \quad t>1.\end{align*} $$